Uji Minda 9.1i – Buku Teks Matematik Tingkatan 3 Bab 9 (Garis Lulus)

Soalan 1:


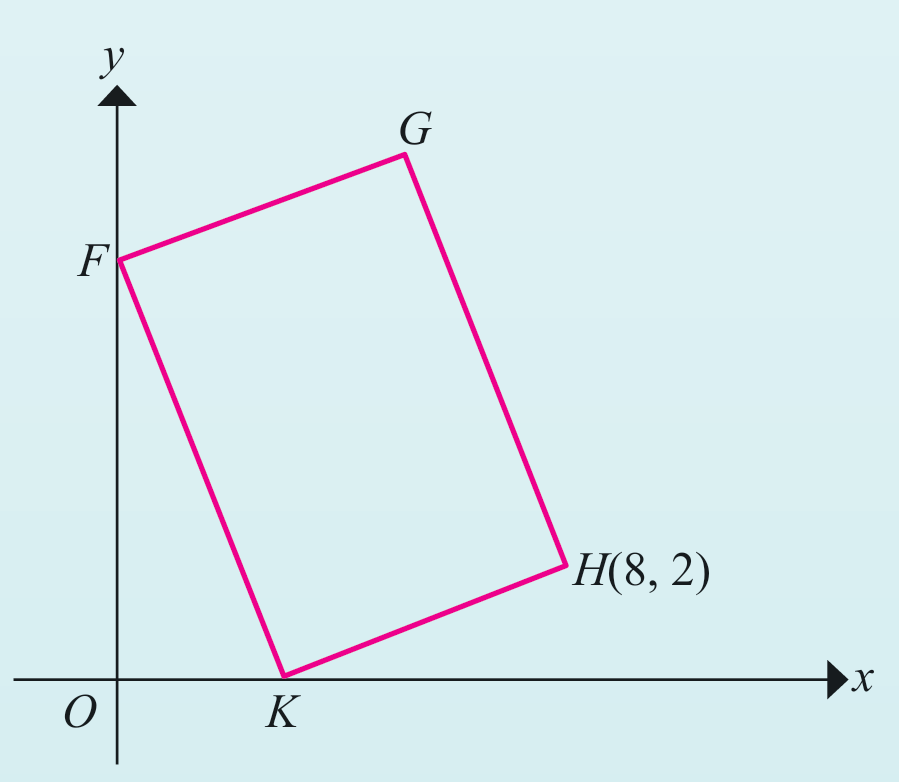
Rajah di sebelah menunjukkan suatu segi empat selari FGHK. Diberi bahawa O ialah asalan dan titik K berada pada paksi-x. Diberi persamaan garis lurus FG ialah 2y = x + 20. Tentukan
(a) kecerunan garis lurus FG.
(b) pintasan-y garis lurus HK.
(c) persamaan garis lurus HK.123


Penyelesaian:
(a)
$$ \begin{aligned} &\begin{aligned} 2 y & =x+20 \\ y & =\frac{1}{2} x+10 \end{aligned}\\ &\text { Kecerunan garis lurus } F G=\frac{1}{2} \end{aligned} $$

(b)
Kecerunan FG = kecerunan HK = ½.
Garis lurus HK melalui titik H (8, 2)
Gantikan nilai m, x dan y ke dalam y = mx + c
$$ \begin{aligned} &\begin{aligned} 2 & =\frac{1}{2}(8)+c \\ 2 & =4+c \\ c & =2-4 \\ & =-2 \end{aligned}\\ &\text { Maka, pintasan-y garis lurus } H K=-2 \end{aligned} $$

(c)
$$ \text { Persamaan garis lurus } H K \text { ialah } y=\frac{1}{2} x-2 \text {. } $$

Soalan 2:


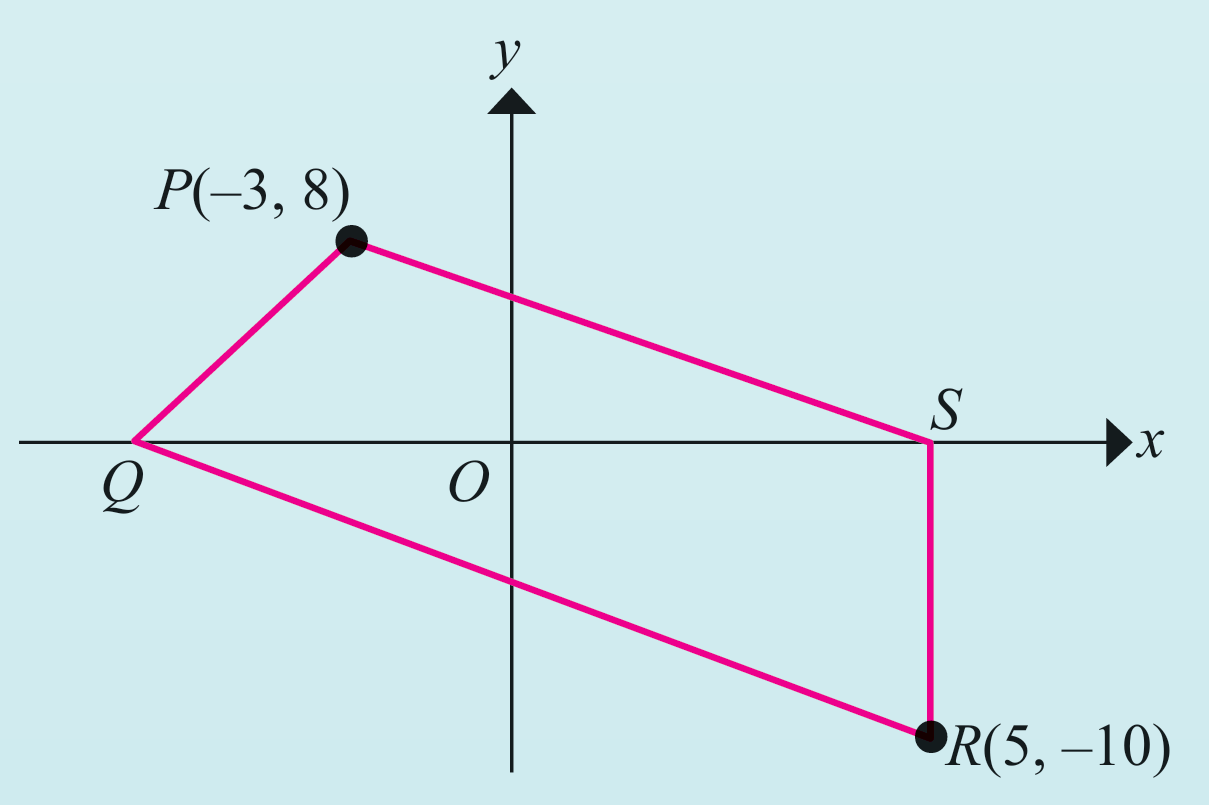
Dalam rajah di sebelah, O ialah asalan dan PQRS ialah satu trapezium dengan PS dan QR adalah selari. Garis lurus RS selari dengan paksi-y, dan titik Q dan S berada pada paksi-x.
Tentukan
(a) koordinat S.
(b) persamaan garis lurus QR.
(c) pintasan-x garis lurus QR.


Penyelesaian:
(a)
Diberi garis lurus RS selari dengan paksi-y,
maka, koordinat x bagi titik R dan S adalah sama = 5.
Pada paksi x, koordinat y = 0, maka koordinat titik S = (5, 0).


(b)
Kecerunan QR = kecerunan PS
$$ \text { Kecerunan } \begin{aligned} P S & =\frac{0-8}{5-(-3)} \\ & =-1 \end{aligned} $$

$$ \begin{aligned} &\text { Garis lurus } Q R \text { melalui titik } R(5,-10)\\ &\begin{aligned} -10 & =-1(5)+c \\ c & =-10+5 \\ & =-5 \end{aligned} \end{aligned} $$

Persamaan garis lurus QR ialah y = – x – 5.

(c)
$$ \begin{aligned} & \text { Apabila } y=0 \\ & 0=-x-5 \\ & x=-5 \end{aligned} $$

Pintasan-x garis lurus QR ialah –5.