Uji Minda 9.1d – Buku Teks Matematik Tingkatan 3 Bab 9 (Garis Lulus)

Soalan 1:
Tentukan sama ada pasangan garis lurus berikut adalah selari.
(a) 3y = –6x + 3 dan y + 2x = 14
(b) 2x + 3y = 3 dan 2x + 6y = 12
(c) y = 2x + 1 dan 8x – 4y = 5
(d) y = –3x + 4 dan 9x + 2y = 12

Penyelesaian:
(a)
$$\begin{aligned} &\begin{gathered} 3 y=-6 x+3 \\ \frac{3 y}{3}=\frac{-6 x}{3}+\frac{3}{3} \\ y=-2 x+1 \end{gathered}\\ &\text { Bandingkan dengan } y=m x+c\\ &\text { Kecerunan }=-2 \end{aligned}$$
$$\begin{aligned} y+2 x & =14 \\ y & =-2 x+14 \\ \text { Kecerunan } & =-2 \end{aligned}$$
Kecerunan kedua-dua garis lurus adalah sama.
maka, 3y = –6x + 3 adalah selari dengan y + 2x = 14.

(b)
$$\begin{aligned} 2 x+3 y & =3 \\ 3 y & =-2 x+3 \\ \frac{3 y}{3} & =\frac{-2 x}{3}+\frac{3}{3} \\ y & =-\frac{2}{3} x+1 \end{aligned}$$

Bandingkan dengan y = mx + c
Kecerunan = -2/3

$$\begin{aligned} 2 x+6 y & =12 \\ 6 y & =-2 x+12 \\ \frac{6 y}{6} & =\frac{-2 x}{6}+\frac{12}{6} \\ y & =-\frac{1}{3} x+2 \\ \text { Kecerunan } & =-\frac{1}{3} \end{aligned}$$

Kecerunan kedua-dua garis lurus adalah tidak sama
maka, 2x + 3y = 3 adalah tidak selari dengan 2x + 6y = 12.

(c)
y = 2x + 1
Bandingkan dengan y = mx + c
Kecerunan = 2
$$\begin{aligned} &\begin{aligned} 8 x-4 y & =5 \\ -4 y & =-8 x+5 \\ \frac{-4 y}{(-4)} & =\frac{-8 x}{(-4)}+\frac{5}{(-4)} \\ y & =2 x-\frac{5}{4} \end{aligned}\\ &\text { Kecerunan }=2 \end{aligned}$$
Kecerunan kedua-dua garis lurus adalah sama.
maka, y = 2x + 1 adalah selari dengan 8x – 4y = 5.

(d)
y = -3x + 4
Bandingkan dengan y = mx + c
Kecerunan= -3
$$\begin{aligned} 9 x+2 y & =12 \\ 2 y & =-9 x+12 \\ \frac{2 y}{2} & =\frac{-9 x}{2}+\frac{12}{2} \\ y & =\frac{-9 x}{2}+6 \\ \text { Kecerunan } & =-\frac{9}{2} \end{aligned}$$
Kecerunan kedua-dua garis lurus adalah tidak sama.
maka, y = -3x + 4 adalah tidak selari dengan 9x + 2y = 12.

Soalan 2:
Tentukan nilai k bagi setiap pasangan garis selari berikut.
(a) y = –3x + 4 dan y + kx = 14
(b) kx + 2y = 7 dan 6x + 2y = 15
(c) 8y = 5x + 1 dan kx – 3y = 8
(d) 3x + ky = 4 dan 2x + y = 3

Penyelesaian:
(a)
y = –3x + 4 selari dengan garis lurus y + kx = 14
y = –3x + 4
Kecerunan = -3

y + kx = 14
y = -kx + 14
Kecerunan = -k

-3 = -k
k = 3

(b)
kx + 2y = 7 selari dengan garis lurus 6x + 2y = 15
$$\begin{aligned} k x+2 y & =7 \\ 2 y & =-k x+7 \\ \frac{2 y}{2} & =\frac{-k x}{2}+\frac{7}{2} \\ y & =-\frac{k}{2} x+\frac{7}{2} \\ \text { Kecerunan } & =-\frac{k}{2} \end{aligned}$$

$$\begin{aligned} &\begin{aligned} 6 x+2 y & =15 \\ 2 y & =-6 x+15 \\ \frac{2 y}{2} & =\frac{-6 x}{2}+\frac{15}{2} \\ y & =-3 x+\frac{15}{2} \end{aligned}\\ &\text { Kecerunan }=-3 \end{aligned}$$
$$\begin{aligned} -\frac{k}{2} & =-3 \\ -k & =-6 \\ k & =6 \end{aligned}$$

(c)
8y = 5x + 1 selari dengan garis lurus kx – 3y = 8
$$\begin{gathered} 8 y=5 x+1 \\ \frac{8 y}{8}=\frac{5 x}{8}+\frac{1}{8} \\ y=\frac{5}{8} x+\frac{1}{8} \\ \text { Kecerunan }=\frac{5}{8} \end{gathered}$$

$$\begin{aligned} & k x-3 y=8 \\ &-3 y=-k x+8 \\ & \frac{-3 y}{(-3)}=\frac{-k x}{(-3)}+\frac{8}{(-3)} \\ & y=\frac{k}{3} x-\frac{8}{3} \\ & \text { Kecerunan }=\frac{k}{3} \end{aligned}$$
$$\begin{aligned} \frac{k}{3} & =\frac{5}{8} \\ k & =\frac{5}{8} \times 3 \\ k & =\frac{15}{8} \end{aligned}$$
(d)
3x + ky = 4 selari dengan garis lurus 2x + y = 3
$$\begin{aligned} 3 x+k y & =4 \\ k y & =-3 x+4 \\ \frac{k y}{k} & =-\frac{3 x}{k}+\frac{4}{k} \\ y & =-\frac{3}{k} x+\frac{4}{k} \\ \text { Kecerunan } & =-\frac{3}{k} \end{aligned}$$

$$\begin{aligned} &\begin{aligned} 2 x+y & =3 \\ y & =-2 x+3 \end{aligned}\\ &\text { Kecerunan }=-2 \end{aligned}$$
$$\begin{aligned} -\frac{3}{k} & =-2 \\ -3 & =-2 k \\ 2 k & =3 \\ k & =\frac{3}{2} \end{aligned}$$

Soalan 3:

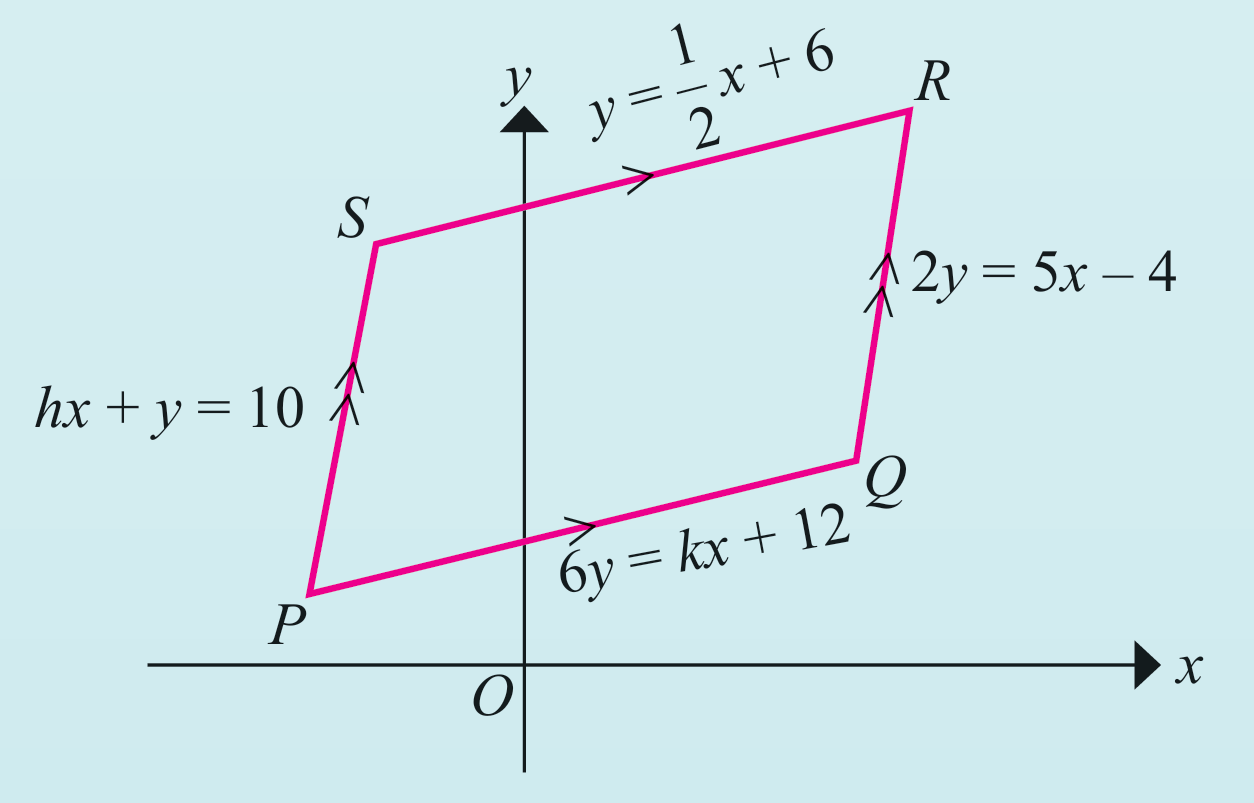
Rajah di sebelah menunjukkan suatu segi empat selari PQRS. Diberi bahawa garis lurus PQ adalah selari dengan SR dan garis lurus PS adalah selari dengan QR. Diberi O ialah asalan. Hitung nilai h dan nilai k.

Penyelesaian:
hx + y = 10 selari dengan garis lurus 2y = 5x – 4

hx + y = 10
y = –hx + 10
Kecerunan = -h
$$\begin{aligned} &\begin{aligned} 2 y & =5 x-4 \\ \frac{2 y}{2} & =\frac{5 x}{2}-\frac{4}{2} \\ y & =\frac{5}{2} x-2 \end{aligned}\\ &\text { Kecerunan }=\frac{5}{2} \end{aligned}$$
$$\begin{aligned} -h & =\frac{5}{2} \\ h & =-\frac{5}{2} \end{aligned}$$

y = ½ x+6  selari dengan garis lurus 6y = kx + 12
$$\begin{aligned} & y=\frac{1}{2} x+6 \\ & \text { Kecerunan }=\frac{1}{2} \end{aligned}$$
$$\begin{aligned} & 6 y=k x+12 \\ & \frac{6 y}{6}=\frac{k x}{6}+\frac{12}{2} \\ & y=\frac{k}{6} x+6 \\ & \text { Kecerunan }=\frac{k}{6} \end{aligned}$$
$$\begin{gathered} \frac{1}{2}=\frac{k}{6} \\ \frac{6}{2}=k \\ k=3 \end{gathered}$$