Cabaran Dinamis – Mahir Diri (Soalan 3 & 4) – Buku Teks Matematik Tingkatan 3 Bab 9 (Garis Lulus)

Soalan 3:


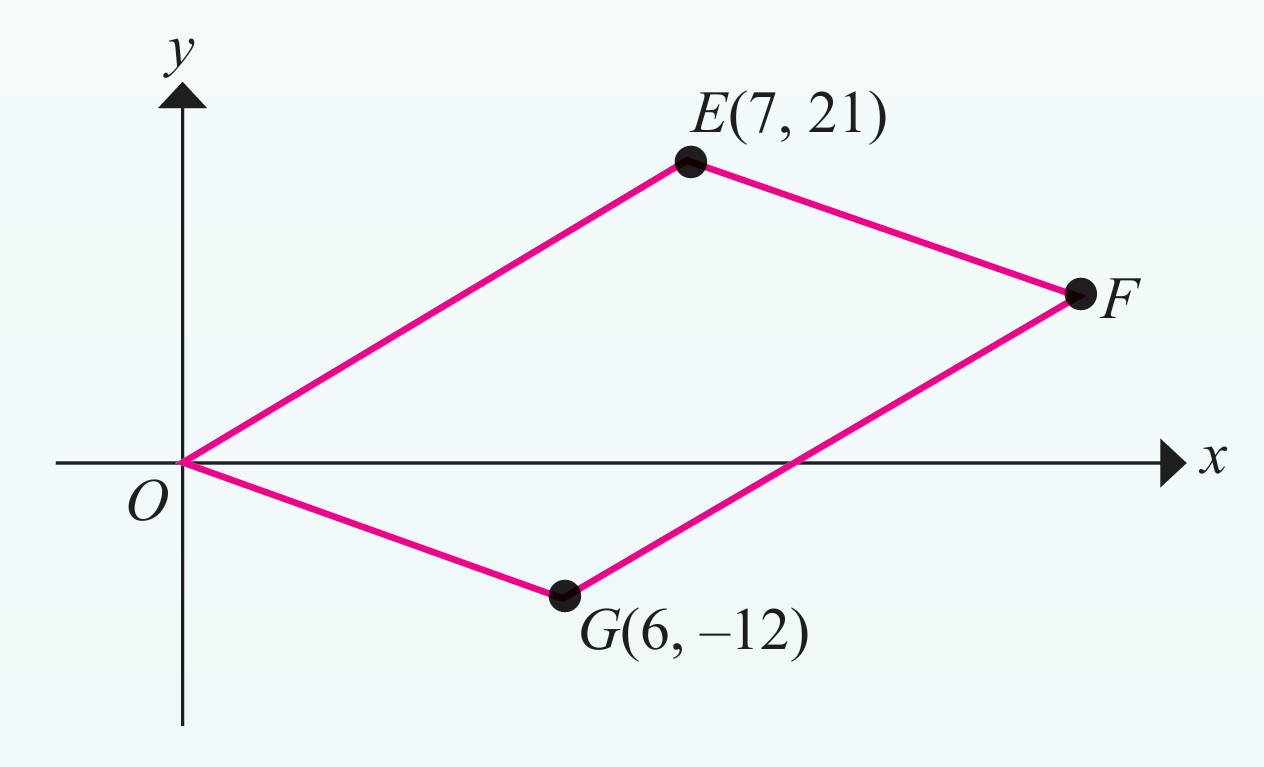
Rajah di sebelah menunjukkan segi empat selari OEFG. Diberi O ialah asalan. Tentukan
(a) persamaan garis lurus OG.
(b) persamaan garis lurus EF.
(c) pintasan-x bagi garis lurus EF.


Penyelesaian:
(a)
$$ \begin{aligned} & \text { Kecerunan } O G=\frac{-12-0}{6-0} \\ & = -2 \\ & \text { Pintasan paksi }-y, c=0 \\ & \text { Persamaan } O G \text { ialah } y=-2 x \end{aligned} $$

(b)
OG selari dengan EF
maka kecerunan OG = kecerunan EF
Garis lurus EF melalui titik E (7, 21)
$$ \begin{aligned} &\begin{aligned} 21 & =-2(7)+c \\ c & =21+14 \\ & =35 \end{aligned}\\ &\text { Persamaan garis lurus } E F \text { ialah } y=-2 x+35 \text {. } \end{aligned} $$

(c)
$$ \begin{aligned} &\begin{aligned} \text { Bila } y & =0 \\ 0 & =-2 x+35 \\ 2 x & =35 \end{aligned}\\ &\text { Pintasan }-x \text { garis lurus } E F=\frac{35}{2} \end{aligned} $$

Soalan 4:


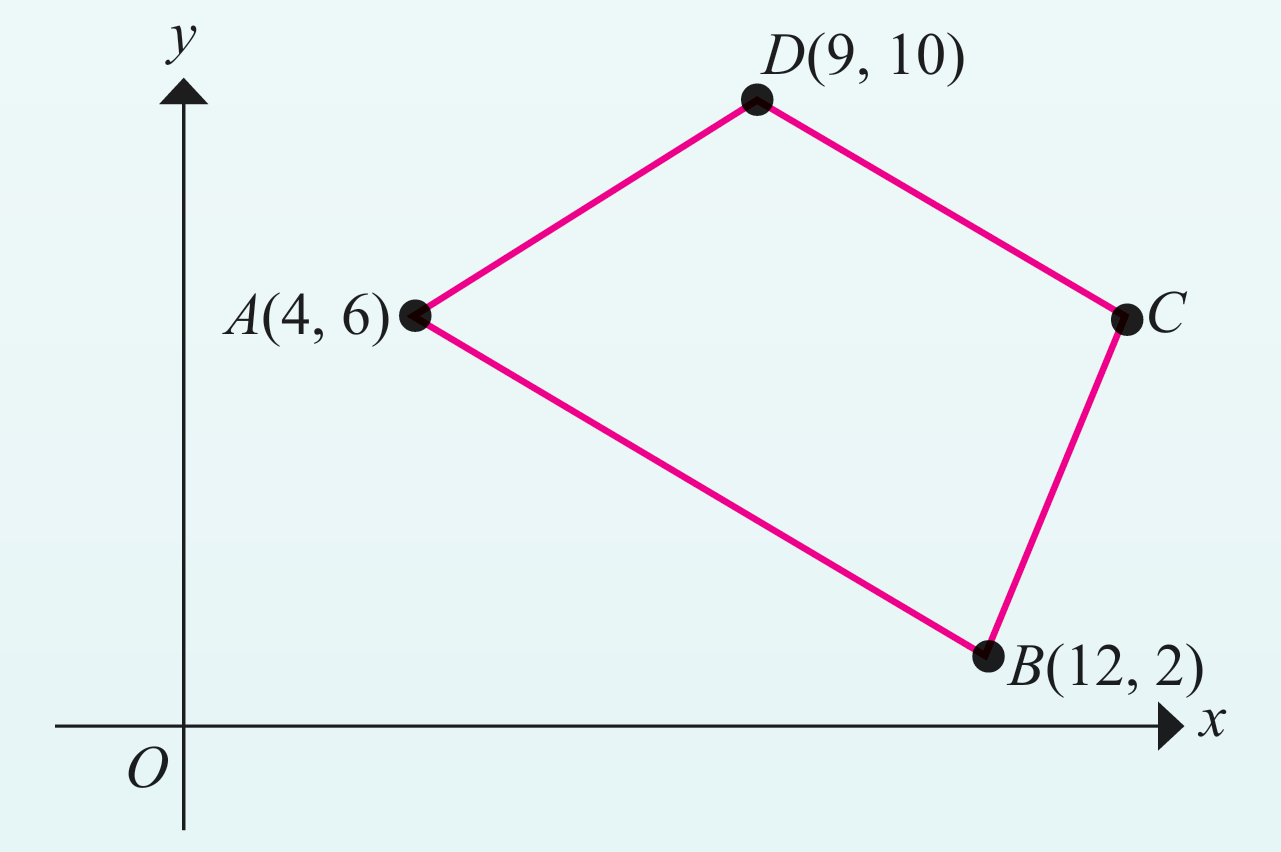
Rajah di sebelah menunjukkan trapezium ABCD dilukis pada satah Cartes. Diberi AB selari dengan DC. Tentukan
(a) persamaan garis lurus AB.
(b) persamaan garis lurus CD.
(c) Adakah garis lurus AB dan garis lurus CD akan bersilang? Nyatakan alasan untuk jawapan anda.


Penyelesaian:
(a)
$$ \text { Kecerunan } \begin{aligned} A B & =\frac{2-6}{12-4} \\ & =\frac{-4}{8} \\ & =-\frac{1}{2} \end{aligned} $$

Gantikan nilai m, titik A(4, 6) ke dalam y = mx + c

$$ \begin{aligned} &\begin{aligned} 6 & =4\left(-\frac{1}{2}\right)+c \\ 6 & =-2+c \\ c & =6+2 \\ & =8 \end{aligned}\\ &\text { Persamaan garis lurus } A B \text { ialah } y=-\frac{1}{2} x+8 \end{aligned} $$


(b)
kecerunan CD = kecerunan AB
$$ \begin{aligned} &\begin{aligned} & \text { Pada titik } D(9,10) \\ & 10=-\frac{1}{2}(9)+c \\ & 10=-\frac{9}{2}+c \\ & c=10+\frac{9}{2} \\ &=\frac{29}{2} \end{aligned}\\ &\text { Persamaan garis lurus } C D \text { ialah } y=-\frac{1}{2} x+\frac{29}{2} \end{aligned} $$

(c) Tidak kerana kedua-dua garis lurus tersebut selari.