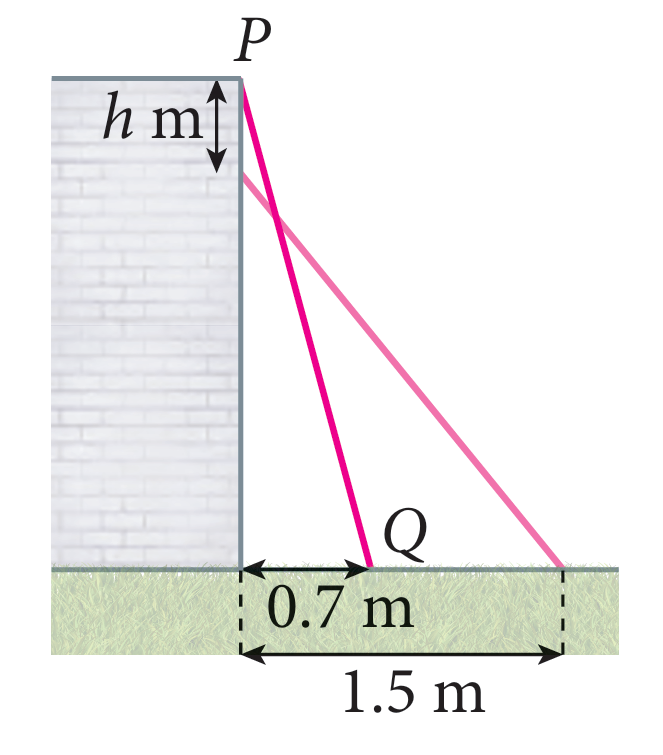
Rajah di sebelah menunjukkan sebuah tangga PQ disandarkan pada dinding. Panjang tangga ialah 2.5 m dan jarak kaki tangga dari dinding ialah 0.7 m. Apabila bahagian atas tangga itu tergelincir ke bawah sebanyak h m, jarak kaki tangga dari dinding ialah 1.5 m. Cari nilai h.
Penyelesaian:
$$
\begin{aligned}
\text { Tinggi dinding } & =\sqrt{2.5^2-0.7^2} \\
& =\sqrt{6.25-0.49} \\
& =\sqrt{5.76} \\
& =2.4 \mathrm{~m}
\end{aligned}
$$
$$
\begin{aligned}
&\text { Tinggi dinding yang disandarkan selepas tangga tergelincir }\\
&\begin{aligned}
& =\sqrt{2.5^2-1.5^2} \\
& =\sqrt{6.25-2.25} \\
& =\sqrt{4} \\
& =2 \mathrm{~m} \\
& \\
& h=2.4-2 \\
& =0.4 \mathrm{~m}
\end{aligned}
\end{aligned}
$$
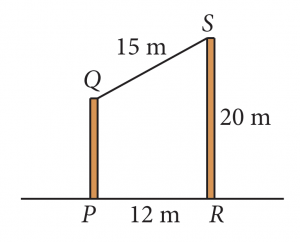
Jarak di antara dua batang tiang tegak, PQ dan RS, yang berada pada tanah mengufuk ialah 12 m. Seutas tali yang panjangnya 15 m diikat pada puncak kedua-dua tiang itu. Jika tinggi tiang RS ialah 20 m, terangkan bagaimana anda mencari tinggi tiang PQ.
Penyelesaian:
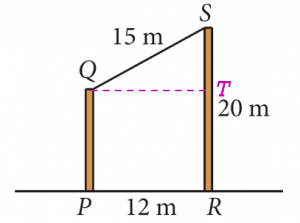
$$
\begin{aligned}
S T^2 & =S Q^2-Q T^2 \\
& =15^2-12^2 \\
& =81 \\
S T & =\sqrt{81} \\
& =9 \mathrm{~m} \\
P Q & =20-9 \\
& =11 \mathrm{~m}
\end{aligned}
$$
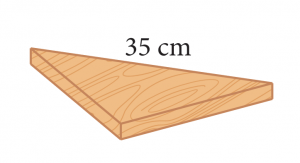
Ali ingin memotong sekeping papan berbentuk segi tiga bersudut tegak. Sisi hipotenus papan itu dikehendaki 35 cm dan dua sisi yang lain dikehendaki dalam nisbah 3 : 4. Terangkan bagaimana anda mencari panjang dua sisi yang lain dan seterusnya membantu Ali memotong papan itu.
Penyelesaian:
$$
\begin{aligned}
&\text { Dengan menggunakan konsep trirangkap Pythagoras, }(3,4,5)\\
&\begin{aligned}
c^2 & =a^2+b^2 \\
5^2 & =3^2+4^2 \\
(5 \times 7)^2 & =(3 \times 7)^2+(4 \times 7)^2 \\
35^2 & =21^2+28^2 \\
35^2 & =441+784 \\
1225 \mathrm{~cm} & =1225 \mathrm{~cm}
\end{aligned}
\end{aligned}
$$
Maka panjang dua sisi yang lain ialah 21 cm dan 28 cm.
Satu gelung benang telah ditanda dengan 12 titik supaya titik-titik bersebelahan adalah sama jarak antara satu sama lain. Terangkan bagaimana anda membentuk sebuah segi tiga bersudut tegak dengan gelung benang itu.
Penyelesaian:
$$
\begin{aligned}
&\text { Dengan menggunakan konsep trirangkap Pythagoras, }(3,4,5)\\
&\begin{aligned}
& c^2=a^2+b^2 \\
& 5^2=3^2+4^2 \\
& 25=9+16 \\
& 25=25
\end{aligned}
\end{aligned}
$$
$$
\begin{aligned}
&\text { Gelung benang mempunyai } 12 \text { titik, }\\
&3+4+5=12
\end{aligned}
$$
