Soalan 1:
Hitung nilai operasi berikut tanpa menggunakan kalkulator.
(a) 8 sin 60° – 3 tan 60°
(b) (tan 30°)(2 kos 30°) + 6 sin 30°
(c) (8 kos 45°)(sin 60°) + (8 sin 45°)(kos 30°)
Penyelesaian:

(a)
$$ \begin{aligned} & 8 \sin 60^{\circ}-3 \tan 60^{\circ} \\ & =8\left(\frac{\sqrt{3}}{2}\right)-3 \sqrt{3} \\ & =4 \sqrt{3}-3 \sqrt{3} \\ & =1 \sqrt{3}=\sqrt{3} \end{aligned} $$
(b)
$$ \begin{aligned} & \left(\tan 30^{\circ}\right)\left(2 \operatorname{kos} 30^{\circ}\right)+6 \sin 30^{\circ} \\ & =\left(\frac{1}{\sqrt{3}}\right)\left[2\left(\frac{\sqrt{3}}{2}\right)\right]+6\left(\frac{1}{2}\right) \\ & =\frac{1}{\sqrt{3}}(\sqrt{3})+3 \\ & =4 \end{aligned} $$
(c)
$$ \begin{aligned} & \left(8 \operatorname{kos} 45^{\circ}\right)\left(\sin 60^{\circ}\right)+\left(8 \sin 45^{\circ}\right)\left(\operatorname{kos} 30^{\circ}\right) \\ & =\left[8\left(\frac{1}{\sqrt{2}}\right)\right]\left(\frac{\sqrt{3}}{2}\right)+\left[8\left(\frac{1}{\sqrt{2}}\right)\right]\left(\frac{\sqrt{3}}{2}\right) \\ & =\frac{4 \sqrt{3}}{\sqrt{2}}+\frac{4 \sqrt{3}}{\sqrt{2}} \\ & =\frac{8 \sqrt{3}}{\sqrt{2}} \\ & =\frac{8 \sqrt{3}}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} \\ & =\frac{8 \sqrt{3} \times 2}{\sqrt{2} \times 2} \\ & =\frac{8 \sqrt{6}}{\sqrt{4}} \\ & =\frac{8 \sqrt{6}}{2} \\ & =4 \sqrt{6} \end{aligned} $$
Hitung nilai operasi berikut tanpa menggunakan kalkulator.
(a) 8 sin 60° – 3 tan 60°
(b) (tan 30°)(2 kos 30°) + 6 sin 30°
(c) (8 kos 45°)(sin 60°) + (8 sin 45°)(kos 30°)
Penyelesaian:

(a)
$$ \begin{aligned} & 8 \sin 60^{\circ}-3 \tan 60^{\circ} \\ & =8\left(\frac{\sqrt{3}}{2}\right)-3 \sqrt{3} \\ & =4 \sqrt{3}-3 \sqrt{3} \\ & =1 \sqrt{3}=\sqrt{3} \end{aligned} $$
(b)
$$ \begin{aligned} & \left(\tan 30^{\circ}\right)\left(2 \operatorname{kos} 30^{\circ}\right)+6 \sin 30^{\circ} \\ & =\left(\frac{1}{\sqrt{3}}\right)\left[2\left(\frac{\sqrt{3}}{2}\right)\right]+6\left(\frac{1}{2}\right) \\ & =\frac{1}{\sqrt{3}}(\sqrt{3})+3 \\ & =4 \end{aligned} $$
(c)
$$ \begin{aligned} & \left(8 \operatorname{kos} 45^{\circ}\right)\left(\sin 60^{\circ}\right)+\left(8 \sin 45^{\circ}\right)\left(\operatorname{kos} 30^{\circ}\right) \\ & =\left[8\left(\frac{1}{\sqrt{2}}\right)\right]\left(\frac{\sqrt{3}}{2}\right)+\left[8\left(\frac{1}{\sqrt{2}}\right)\right]\left(\frac{\sqrt{3}}{2}\right) \\ & =\frac{4 \sqrt{3}}{\sqrt{2}}+\frac{4 \sqrt{3}}{\sqrt{2}} \\ & =\frac{8 \sqrt{3}}{\sqrt{2}} \\ & =\frac{8 \sqrt{3}}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} \\ & =\frac{8 \sqrt{3} \times 2}{\sqrt{2} \times 2} \\ & =\frac{8 \sqrt{6}}{\sqrt{4}} \\ & =\frac{8 \sqrt{6}}{2} \\ & =4 \sqrt{6} \end{aligned} $$
Soalan 2:
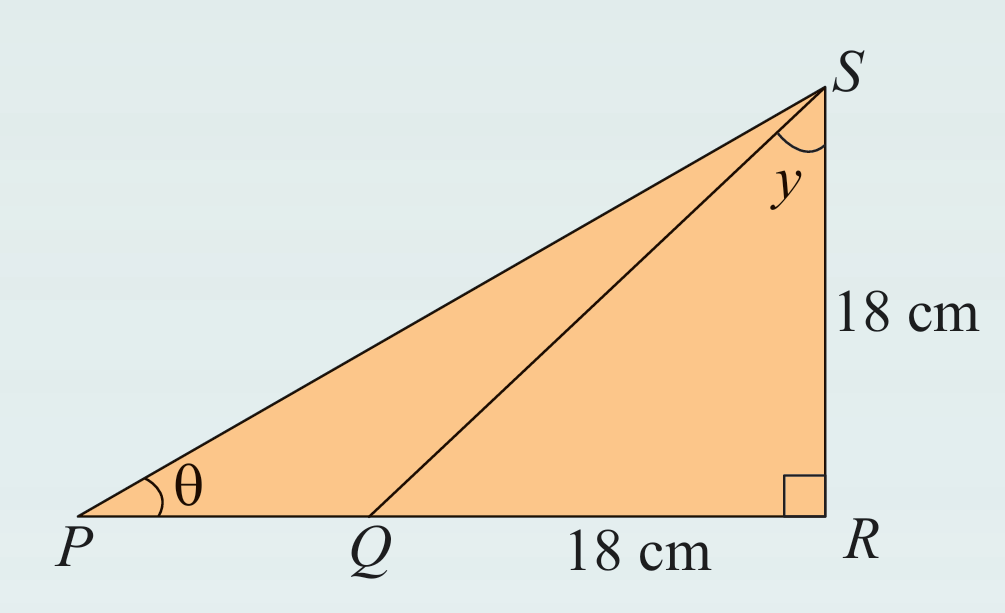
Rajah di sebelah menunjukkan segi tiga bersudut tegak PRS. PQR ialah garis lurus. Diberi bahawa QR = RS = 18 cm dan tan θ = 3/5. Hitung
(a) panjang PQ, dalam cm
(b) panjang PS, dalam cm, betul kepada integer terdekat
(c) nilai y
Penyelesaian:
(a)
$$ \begin{aligned} \tan \theta & =\frac{3}{5} \\ \frac{S R}{P R} & =\frac{3}{5} \\ \frac{18}{P Q+18} & =\frac{3}{5} \\ 18 \times 5 & =3(P Q+18) \\ 90 & =3 P Q+54 \\ 3 P Q & =90-54 \\ 3 P Q & =36 \\ P Q & =\frac{36}{3} \\ P Q & =12 \mathrm{~cm} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Guna teorem Pythagoras, }\\ &\begin{aligned} P S^2 & =P R^2+R S^2 \\ P S & =\sqrt{(12+18)^2+18^2} \\ & =\sqrt{1224} \\ & =34.99 \\ & \approx 35 \mathrm{~cm} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} &\triangle Q R S \text { ialah segi tiga sama kaki }\\ &\begin{aligned} y & =\left(180^{\circ}-90^{\circ}\right) \div 2 \\ & =45^{\circ} \end{aligned} \end{aligned} $$

Rajah di sebelah menunjukkan segi tiga bersudut tegak PRS. PQR ialah garis lurus. Diberi bahawa QR = RS = 18 cm dan tan θ = 3/5. Hitung
(a) panjang PQ, dalam cm
(b) panjang PS, dalam cm, betul kepada integer terdekat
(c) nilai y
Penyelesaian:
(a)
$$ \begin{aligned} \tan \theta & =\frac{3}{5} \\ \frac{S R}{P R} & =\frac{3}{5} \\ \frac{18}{P Q+18} & =\frac{3}{5} \\ 18 \times 5 & =3(P Q+18) \\ 90 & =3 P Q+54 \\ 3 P Q & =90-54 \\ 3 P Q & =36 \\ P Q & =\frac{36}{3} \\ P Q & =12 \mathrm{~cm} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Guna teorem Pythagoras, }\\ &\begin{aligned} P S^2 & =P R^2+R S^2 \\ P S & =\sqrt{(12+18)^2+18^2} \\ & =\sqrt{1224} \\ & =34.99 \\ & \approx 35 \mathrm{~cm} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} &\triangle Q R S \text { ialah segi tiga sama kaki }\\ &\begin{aligned} y & =\left(180^{\circ}-90^{\circ}\right) \div 2 \\ & =45^{\circ} \end{aligned} \end{aligned} $$
Soalan 3:
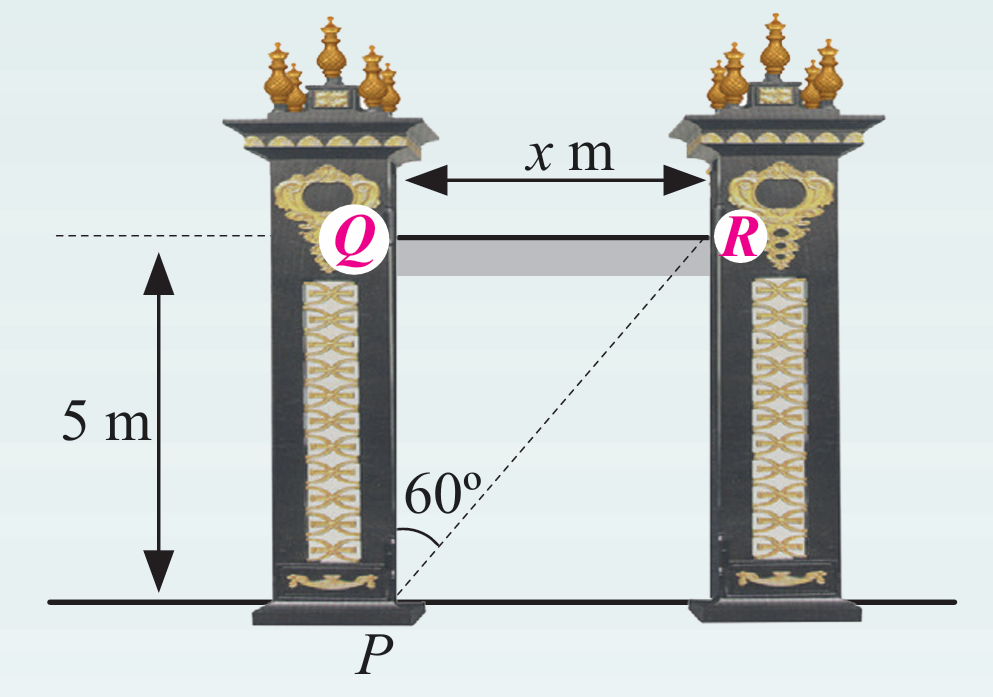
Sebuah pintu gerbang mempunyai dua tiang mercu yang dihubungkan dengan satu jambatan mengufuk dengan jarak x meter. Jika tinggi tegak jambatan dari permukaan tanah ialah 5 m dan sudut di antara tiang PQ dengan garis condong PR ialah 60°, tentukan nilai x, dalam meter.
Penyelesaian:
$$ \begin{aligned} \tan & =\frac{\text { sisi bertentangan }}{\text { sisi bersebelahan }} \\ \tan 60^{\circ} & =\frac{Q R}{P Q} \\ \tan 60^{\circ} & =\frac{x}{5} \\ 5 \tan 60^{\circ} & =x \\ 8.66 & =x \\ x & =8.66 \mathrm{~m} \end{aligned} $$

Sebuah pintu gerbang mempunyai dua tiang mercu yang dihubungkan dengan satu jambatan mengufuk dengan jarak x meter. Jika tinggi tegak jambatan dari permukaan tanah ialah 5 m dan sudut di antara tiang PQ dengan garis condong PR ialah 60°, tentukan nilai x, dalam meter.
Penyelesaian:
$$ \begin{aligned} \tan & =\frac{\text { sisi bertentangan }}{\text { sisi bersebelahan }} \\ \tan 60^{\circ} & =\frac{Q R}{P Q} \\ \tan 60^{\circ} & =\frac{x}{5} \\ 5 \tan 60^{\circ} & =x \\ 8.66 & =x \\ x & =8.66 \mathrm{~m} \end{aligned} $$