Soalan 1:
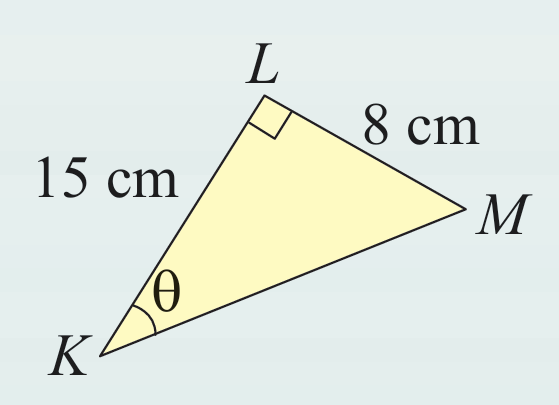
Rajah di sebelah menunjukkan segi tiga bersudut tegak KLM. Hitung
(a) θ dalam darjah dan minit.
(b) sin (90°– θ)
(c) kos (90°– θ)
Penyelesaian:
(a)
$$ \begin{aligned} \tan & =\frac{\text { sisi bertentangan }}{\text { sisi bersebelahan }} \\ \tan \theta & =\frac{L M}{K L} \\ \theta & =\tan ^{-1} \frac{L M}{K L} \\ & =\tan ^{-1}\left(\frac{8}{15}\right) \\ & =28^{\circ} 4^{\prime} \end{aligned} $$
(b)
$$ \begin{aligned} \angle K L M+\angle L M K+\angle M K L & =180^{\circ} \\ 90^{\circ}+\angle L M K+\theta & =180^{\circ} \\ \angle L M K & =180^{\circ}-90^{\circ}-\theta \\ \angle L M K & =90^{\circ}-\theta \end{aligned} $$
$$ \begin{aligned} \sin \left(90^{\circ}-\theta\right) & =\sin \angle L M K \\ & =\frac{K L}{K M} \\ & =\frac{15}{K M} \\ & =\frac{15}{17} \end{aligned} $$
$$ \begin{aligned} &\text { Guna teorem Pythagoras, }\\ &\begin{aligned} K M^2 & =K L^2+L M^2 \\ K M & =\sqrt{15^2+8^2} \\ & =\sqrt{289} \\ & =17 \mathrm{~cm} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} \operatorname{kos}\left(90^{\circ}-\theta\right) & =\operatorname{kos} \angle L M K \\ & =\frac{L M}{K M} \\ & =\frac{8}{17} \end{aligned} $$

Rajah di sebelah menunjukkan segi tiga bersudut tegak KLM. Hitung
(a) θ dalam darjah dan minit.
(b) sin (90°– θ)
(c) kos (90°– θ)
Penyelesaian:
(a)
$$ \begin{aligned} \tan & =\frac{\text { sisi bertentangan }}{\text { sisi bersebelahan }} \\ \tan \theta & =\frac{L M}{K L} \\ \theta & =\tan ^{-1} \frac{L M}{K L} \\ & =\tan ^{-1}\left(\frac{8}{15}\right) \\ & =28^{\circ} 4^{\prime} \end{aligned} $$
(b)
$$ \begin{aligned} \angle K L M+\angle L M K+\angle M K L & =180^{\circ} \\ 90^{\circ}+\angle L M K+\theta & =180^{\circ} \\ \angle L M K & =180^{\circ}-90^{\circ}-\theta \\ \angle L M K & =90^{\circ}-\theta \end{aligned} $$
$$ \begin{aligned} \sin \left(90^{\circ}-\theta\right) & =\sin \angle L M K \\ & =\frac{K L}{K M} \\ & =\frac{15}{K M} \\ & =\frac{15}{17} \end{aligned} $$
$$ \begin{aligned} &\text { Guna teorem Pythagoras, }\\ &\begin{aligned} K M^2 & =K L^2+L M^2 \\ K M & =\sqrt{15^2+8^2} \\ & =\sqrt{289} \\ & =17 \mathrm{~cm} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} \operatorname{kos}\left(90^{\circ}-\theta\right) & =\operatorname{kos} \angle L M K \\ & =\frac{L M}{K M} \\ & =\frac{8}{17} \end{aligned} $$
Soalan 2:
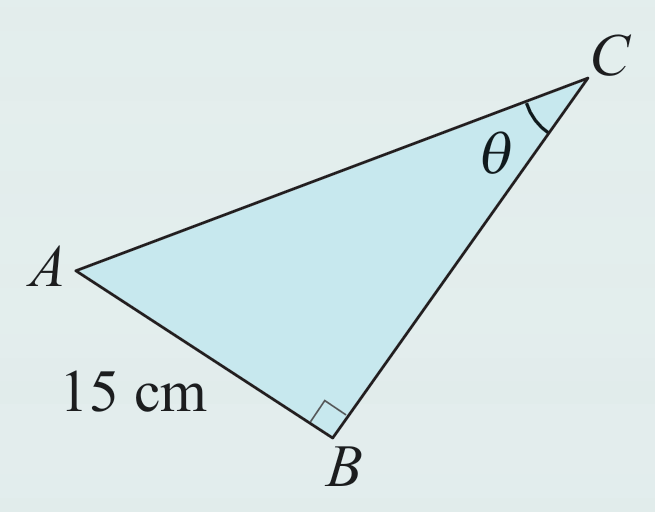
Rajah di sebelah menunjukkan segi tiga bersudut tegak ABC. Diberi bahawa tan θ = 5/12. Hitung
(a) panjang AC, dalam cm
(b) nilai tan (90°– θ)
(c) θ dalam darjah betul kepada tiga angka bererti
Penyelesaian:
(a)
$$ \begin{aligned} \tan \theta & =\frac{A B}{B C} \\ \frac{A B}{B C} & =\frac{5}{12} \\ \frac{15}{B C} & =\frac{5}{12} \\ 15 \times \frac{12}{5} & =B C \\ 36 & =B C \\ B C & =36 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} A C^2 & =A B^2+B C^2 \\ A C & =\sqrt{15^2+36^2} \\ & =\sqrt{1521} \\ & =39 \mathrm{~cm} \end{aligned} $$
(b)
$$ \begin{aligned} \tan \left(90^{\circ}-\theta\right) & =\tan \angle C A B \\ & =\frac{B C}{A B} \\ & =\frac{36}{15} \\ & =\frac{12}{5} \end{aligned} $$
(c)
$$ \begin{aligned} \tan & =\frac{\text { sisi bertentangan }}{\text { sisi bersebelahan }} \\ \tan \theta & =\frac{A B}{B C} \\ \theta & =\tan ^{-1} \frac{A B}{B C} \\ & =\tan ^{-1}\left(\frac{15}{36}\right) \\ & =22.6^{\circ} \end{aligned} $$

Rajah di sebelah menunjukkan segi tiga bersudut tegak ABC. Diberi bahawa tan θ = 5/12. Hitung
(a) panjang AC, dalam cm
(b) nilai tan (90°– θ)
(c) θ dalam darjah betul kepada tiga angka bererti
Penyelesaian:
(a)
$$ \begin{aligned} \tan \theta & =\frac{A B}{B C} \\ \frac{A B}{B C} & =\frac{5}{12} \\ \frac{15}{B C} & =\frac{5}{12} \\ 15 \times \frac{12}{5} & =B C \\ 36 & =B C \\ B C & =36 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} A C^2 & =A B^2+B C^2 \\ A C & =\sqrt{15^2+36^2} \\ & =\sqrt{1521} \\ & =39 \mathrm{~cm} \end{aligned} $$
(b)
$$ \begin{aligned} \tan \left(90^{\circ}-\theta\right) & =\tan \angle C A B \\ & =\frac{B C}{A B} \\ & =\frac{36}{15} \\ & =\frac{12}{5} \end{aligned} $$
(c)
$$ \begin{aligned} \tan & =\frac{\text { sisi bertentangan }}{\text { sisi bersebelahan }} \\ \tan \theta & =\frac{A B}{B C} \\ \theta & =\tan ^{-1} \frac{A B}{B C} \\ & =\tan ^{-1}\left(\frac{15}{36}\right) \\ & =22.6^{\circ} \end{aligned} $$
Soalan 3:
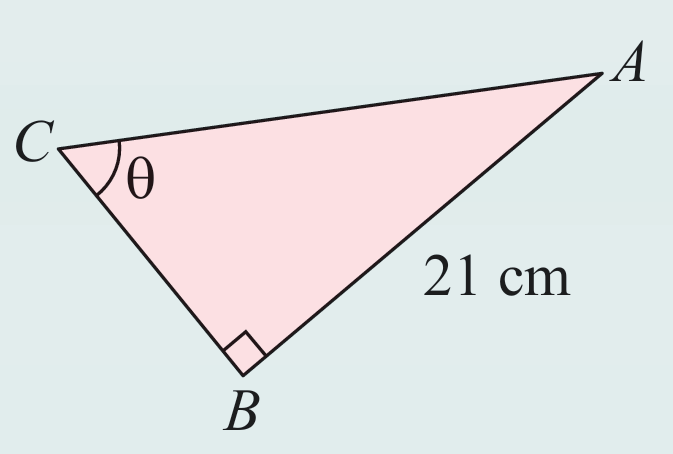
Rajah di sebelah menunjukkan segi tiga bersudut tegak ABC. Diberi bahawa AB = 21 cm dan sin θ = 7/9. Hitung
(a) panjang AC dalam cm
(b) nilai ∠BAC. Nyatakan jawapan anda dalam darjah terdekat
Penyelesaian:
(a)
$$ \begin{aligned} \sin & =\frac{\text { sisi bertentangan }}{\text { hipotenus }} \\ \sin \theta & =\frac{A B}{A C} \\ \frac{A B}{A C} & =\frac{7}{9} \\ \frac{21}{A C} & =\frac{7}{9} \\ 21 \times \frac{9}{7} & =A C \\ 27 & =A C \\ A C & =27 \mathrm{~cm} \end{aligned} $$
(b)
$$ \begin{aligned} \text { kos } & =\frac{\text { sisi bersebelahan }}{\text { hipotenus }} \\ \text { kos } \angle B A C & =\frac{A B}{A C} \\ & =\frac{21}{27} \\ \angle B A C & =\operatorname{kos}^{-1}\left(\frac{21}{27}\right) \\ \angle B A C & =39^{\circ} \end{aligned} $$

Rajah di sebelah menunjukkan segi tiga bersudut tegak ABC. Diberi bahawa AB = 21 cm dan sin θ = 7/9. Hitung
(a) panjang AC dalam cm
(b) nilai ∠BAC. Nyatakan jawapan anda dalam darjah terdekat
Penyelesaian:
(a)
$$ \begin{aligned} \sin & =\frac{\text { sisi bertentangan }}{\text { hipotenus }} \\ \sin \theta & =\frac{A B}{A C} \\ \frac{A B}{A C} & =\frac{7}{9} \\ \frac{21}{A C} & =\frac{7}{9} \\ 21 \times \frac{9}{7} & =A C \\ 27 & =A C \\ A C & =27 \mathrm{~cm} \end{aligned} $$
(b)
$$ \begin{aligned} \text { kos } & =\frac{\text { sisi bersebelahan }}{\text { hipotenus }} \\ \text { kos } \angle B A C & =\frac{A B}{A C} \\ & =\frac{21}{27} \\ \angle B A C & =\operatorname{kos}^{-1}\left(\frac{21}{27}\right) \\ \angle B A C & =39^{\circ} \end{aligned} $$
Soalan 4:
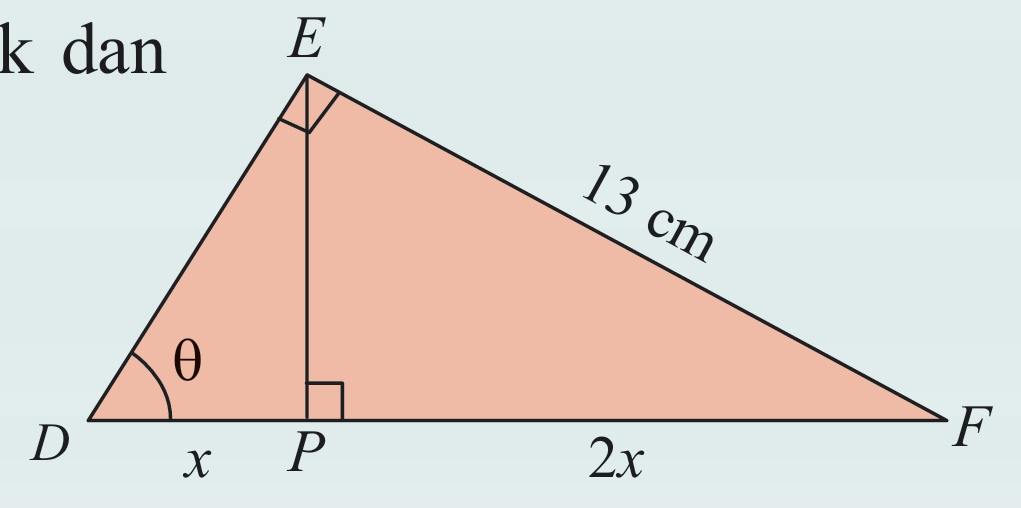
Dalam rajah di sebelah, DEF ialah segi tiga bersudut tegak dan DPF ialah garis lurus. Diberi PE = 5 cm. Hitung nilai
(a) x dalam cm
(b) θ dalam darjah dan minit
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Guna teorem Pythagoras, }\\ &\begin{aligned} E F^2 & =P E^2+P F^2 \\ 13^2 & =5^2+(2 x)^2 \\ 13^2-5^2 & =4 x^2 \\ 169-25 & =4 x^2 \\ 144 & =4 x^2 \\ \frac{144}{4} & =x^2 \\ 36 & =x^2 \\ \sqrt{36} & =x \\ x & =6 \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Bagi } \triangle D E P \text {, }\\ &\begin{aligned} \tan \theta & =\frac{P E}{D P} \\ \theta & =\tan ^{-1}\left(\frac{5}{6}\right) \\ & =39^{\circ} 48^{\prime} \end{aligned} \end{aligned} $$

Dalam rajah di sebelah, DEF ialah segi tiga bersudut tegak dan DPF ialah garis lurus. Diberi PE = 5 cm. Hitung nilai
(a) x dalam cm
(b) θ dalam darjah dan minit
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Guna teorem Pythagoras, }\\ &\begin{aligned} E F^2 & =P E^2+P F^2 \\ 13^2 & =5^2+(2 x)^2 \\ 13^2-5^2 & =4 x^2 \\ 169-25 & =4 x^2 \\ 144 & =4 x^2 \\ \frac{144}{4} & =x^2 \\ 36 & =x^2 \\ \sqrt{36} & =x \\ x & =6 \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Bagi } \triangle D E P \text {, }\\ &\begin{aligned} \tan \theta & =\frac{P E}{D P} \\ \theta & =\tan ^{-1}\left(\frac{5}{6}\right) \\ & =39^{\circ} 48^{\prime} \end{aligned} \end{aligned} $$