Soalan 1:
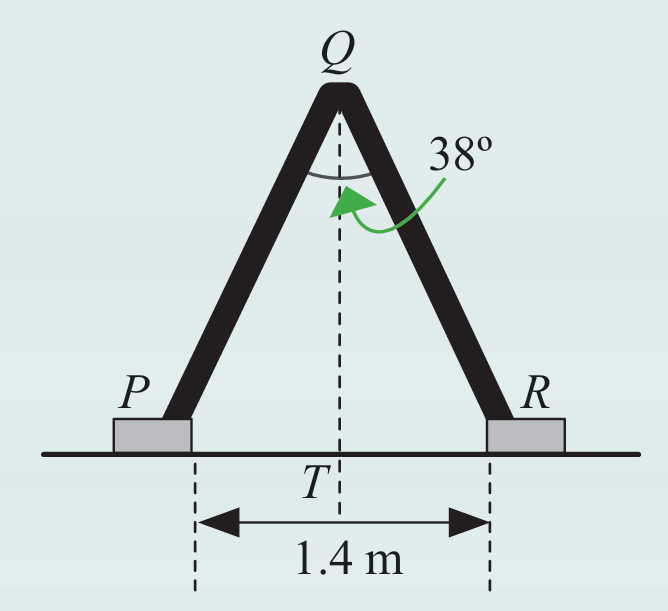
Sebuah tangga lipat yang diletakkan di atas lantai membentuk segi tiga sama kaki PQR seperti dalam rajah di sebelah. Diberi bahawa T ialah titik tengah PR, ∠PQR = 38° dan panjang PR = 1.4 m. Hitungkan panjang PQ, betul kepada dua tempat perpuluhan.
Penyelesaian:
$$ \text { Diberi } \triangle P Q R \text { ialah sebuah segi tiga sama kaki, } $$
$$ \text { maka, } \angle P Q T=\angle R Q T=\frac{1}{2}\left(38^{\circ}\right)=19^{\circ} $$
$$ \begin{aligned} \sin \angle P Q T & =\frac{\text { Sisi bertentangan }}{\text { hipotenus }} \\ \sin \angle P Q T & =\frac{P T}{P Q} \\ \sin 19^{\circ} & =\frac{1.4 \div 0.2}{P Q} \\ P Q & =\frac{0.7}{\sin 19^{\circ}} \\ & =2.15 \mathrm{~m} \end{aligned} $$

Sebuah tangga lipat yang diletakkan di atas lantai membentuk segi tiga sama kaki PQR seperti dalam rajah di sebelah. Diberi bahawa T ialah titik tengah PR, ∠PQR = 38° dan panjang PR = 1.4 m. Hitungkan panjang PQ, betul kepada dua tempat perpuluhan.
Penyelesaian:
$$ \text { Diberi } \triangle P Q R \text { ialah sebuah segi tiga sama kaki, } $$
$$ \text { maka, } \angle P Q T=\angle R Q T=\frac{1}{2}\left(38^{\circ}\right)=19^{\circ} $$
$$ \begin{aligned} \sin \angle P Q T & =\frac{\text { Sisi bertentangan }}{\text { hipotenus }} \\ \sin \angle P Q T & =\frac{P T}{P Q} \\ \sin 19^{\circ} & =\frac{1.4 \div 0.2}{P Q} \\ P Q & =\frac{0.7}{\sin 19^{\circ}} \\ & =2.15 \mathrm{~m} \end{aligned} $$
Soalan 2:
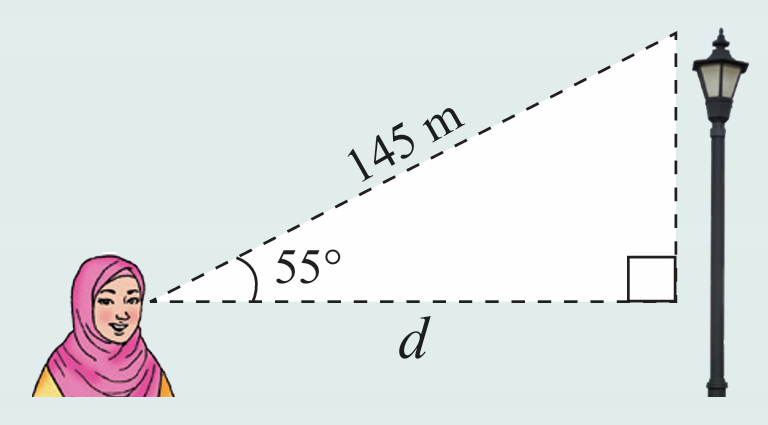
Rajah di sebelah menunjukkan Aisyah yang sedang memerhatikan sebatang tiang lampu. Diberi bahawa sudut dongak hujung tiang lampu dari penglihatan Aisyah ialah 55° dan jarak di antara mata Aisyah dengan hujung tiang lampu ialah 145 meter. Hitung jarak mengufuk, d dalam meter. Nyatakan jawapan betul kepada tiga angka bererti.
Penyelesaian:
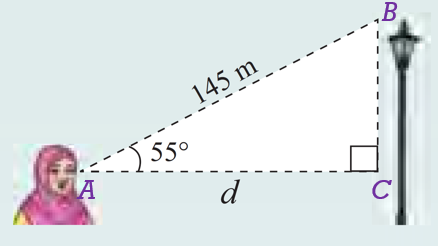
$$ \begin{aligned} \operatorname{kos} \angle B A C & =\frac{\text { Sisi bersebelahan }}{\text { hipotenus }} \\ \operatorname{kos} \angle B A C & =\frac{A C}{A B} \\ \operatorname{kos} 55^{\circ} & =\frac{d}{145} \\ 145 \operatorname{kos} 55^{\circ} & =d \\ 83.2 & =d \\ d & =83.2 \mathrm{~m} \end{aligned} $$

Rajah di sebelah menunjukkan Aisyah yang sedang memerhatikan sebatang tiang lampu. Diberi bahawa sudut dongak hujung tiang lampu dari penglihatan Aisyah ialah 55° dan jarak di antara mata Aisyah dengan hujung tiang lampu ialah 145 meter. Hitung jarak mengufuk, d dalam meter. Nyatakan jawapan betul kepada tiga angka bererti.
Penyelesaian:

$$ \begin{aligned} \operatorname{kos} \angle B A C & =\frac{\text { Sisi bersebelahan }}{\text { hipotenus }} \\ \operatorname{kos} \angle B A C & =\frac{A C}{A B} \\ \operatorname{kos} 55^{\circ} & =\frac{d}{145} \\ 145 \operatorname{kos} 55^{\circ} & =d \\ 83.2 & =d \\ d & =83.2 \mathrm{~m} \end{aligned} $$
Soalan 3:
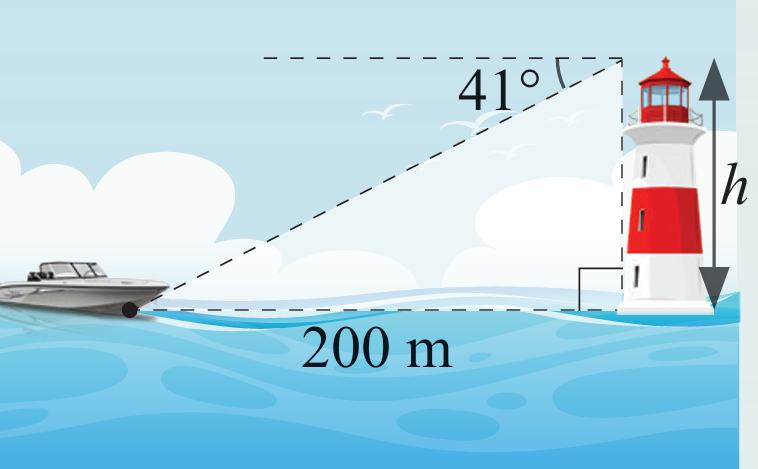
Rajah di sebelah menunjukkan kedudukan sebuah kapal dan rumah api. Diberi bahawa sudut tunduk kapal dari rumah api ialah 41° dan jarak mengufuk di antara rumah api dengan kapal ialah 200 m. Hitung tinggi rumah api, h dalam meter. Nyatakan jawapan betul kepada empat angka bererti.
Penyelesaian:
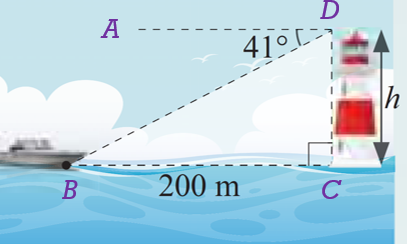
$$ \begin{aligned} \angle B D C & =90^{\circ}-41^{\circ} \\ & =49^{\circ} \end{aligned} $$
$$ \begin{aligned} \tan \angle B D C & =\frac{\text { Sisi bertentangan }}{\text { Sisi bersebelahan }} \\ \tan \angle B D C & =\frac{B C}{D C} \\ \tan 49^{\circ} & =\frac{200}{h} \\ h & =\frac{200}{\tan 49^{\circ}} \\ & =173.9 \mathrm{~m} \end{aligned} $$

Rajah di sebelah menunjukkan kedudukan sebuah kapal dan rumah api. Diberi bahawa sudut tunduk kapal dari rumah api ialah 41° dan jarak mengufuk di antara rumah api dengan kapal ialah 200 m. Hitung tinggi rumah api, h dalam meter. Nyatakan jawapan betul kepada empat angka bererti.
Penyelesaian:

$$ \begin{aligned} \angle B D C & =90^{\circ}-41^{\circ} \\ & =49^{\circ} \end{aligned} $$
$$ \begin{aligned} \tan \angle B D C & =\frac{\text { Sisi bertentangan }}{\text { Sisi bersebelahan }} \\ \tan \angle B D C & =\frac{B C}{D C} \\ \tan 49^{\circ} & =\frac{200}{h} \\ h & =\frac{200}{\tan 49^{\circ}} \\ & =173.9 \mathrm{~m} \end{aligned} $$
Soalan 4:
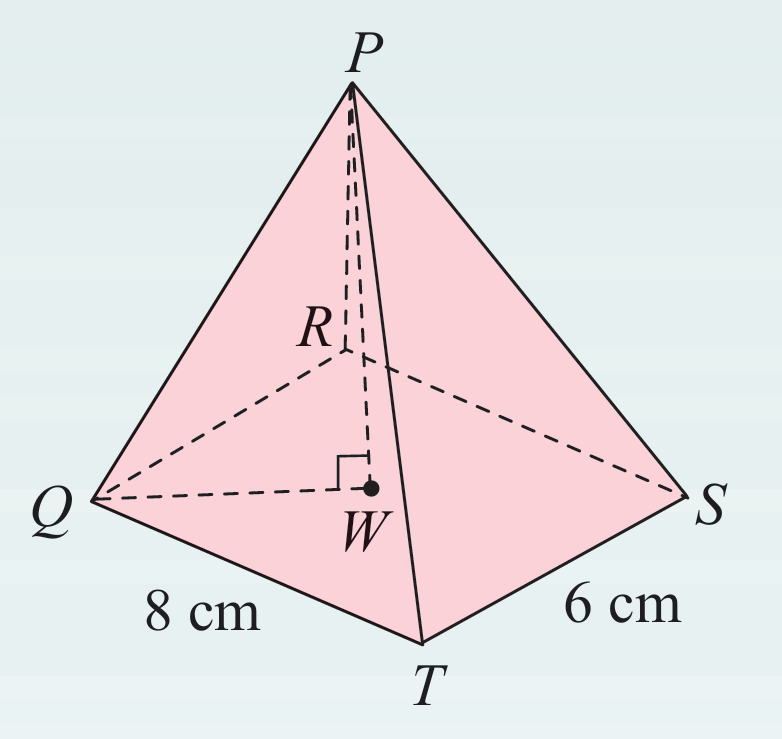
Sebuah piramid tegak PQRST mempunyai tapak segi empat tepat QRST. Diberi bahawa W ialah titik tengah QS dan RT. Panjang QT = 8 cm, TS = 6 cm dan titik P terletak tegak di atas titik W. Hitung
(a) panjang PT, dalam cm, jika PW = 12 cm
(b) nilai ∠PTR
Penyelesaian:
(a)
Diberi QRST ialah tapak segi empat tepat. Diberi 𝑊 ialah titik tengah QS dan RT.
$$ \begin{aligned} &\text { Dengan mengguna teorem Pythagoras, }\\ &\begin{aligned} Q S^2 & =Q T^2+S T^2 \\ & =8^2+6^2 \\ & =100 \\ Q S & =\sqrt{100} \\ & =10 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \begin{aligned} Q S & =R T \\ \text { Maka, } W T & =\frac{1}{2} Q S \\ & =\frac{1}{2}(10) \\ & =5 \mathrm{~cm} \end{aligned} $$
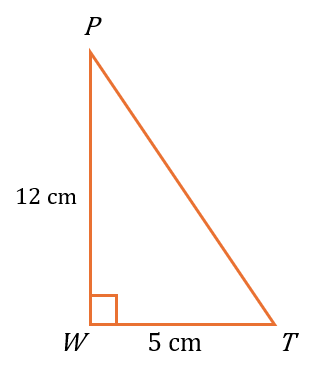
$$ \begin{aligned} P T^2 & =P W^2+W T^2 \\ & =12^2+5^2 \\ & =169 \\ P T & =\sqrt{169} \\ & =13 \mathrm{~cm} \end{aligned} $$
(b)
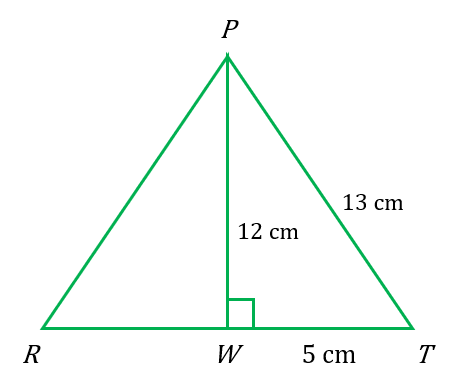
$$ \begin{aligned} & \angle P T R=\angle P T W \\ & \begin{aligned} \tan \angle P T R & =\frac{\text { Sisi bertentangan }}{\text { Sisi bersebelahan }} \\ \tan \angle P T R & =\frac{P W}{W T} \\ & =\tan ^{-1} \frac{P W}{W T} \\ & =\tan ^{-1} \frac{12}{5} \\ & =67.4^{\circ} \end{aligned} \end{aligned} $$

Sebuah piramid tegak PQRST mempunyai tapak segi empat tepat QRST. Diberi bahawa W ialah titik tengah QS dan RT. Panjang QT = 8 cm, TS = 6 cm dan titik P terletak tegak di atas titik W. Hitung
(a) panjang PT, dalam cm, jika PW = 12 cm
(b) nilai ∠PTR
Penyelesaian:
(a)
Diberi QRST ialah tapak segi empat tepat. Diberi 𝑊 ialah titik tengah QS dan RT.
$$ \begin{aligned} &\text { Dengan mengguna teorem Pythagoras, }\\ &\begin{aligned} Q S^2 & =Q T^2+S T^2 \\ & =8^2+6^2 \\ & =100 \\ Q S & =\sqrt{100} \\ & =10 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \begin{aligned} Q S & =R T \\ \text { Maka, } W T & =\frac{1}{2} Q S \\ & =\frac{1}{2}(10) \\ & =5 \mathrm{~cm} \end{aligned} $$

$$ \begin{aligned} P T^2 & =P W^2+W T^2 \\ & =12^2+5^2 \\ & =169 \\ P T & =\sqrt{169} \\ & =13 \mathrm{~cm} \end{aligned} $$
(b)

$$ \begin{aligned} & \angle P T R=\angle P T W \\ & \begin{aligned} \tan \angle P T R & =\frac{\text { Sisi bertentangan }}{\text { Sisi bersebelahan }} \\ \tan \angle P T R & =\frac{P W}{W T} \\ & =\tan ^{-1} \frac{P W}{W T} \\ & =\tan ^{-1} \frac{12}{5} \\ & =67.4^{\circ} \end{aligned} \end{aligned} $$