Soalan 8:
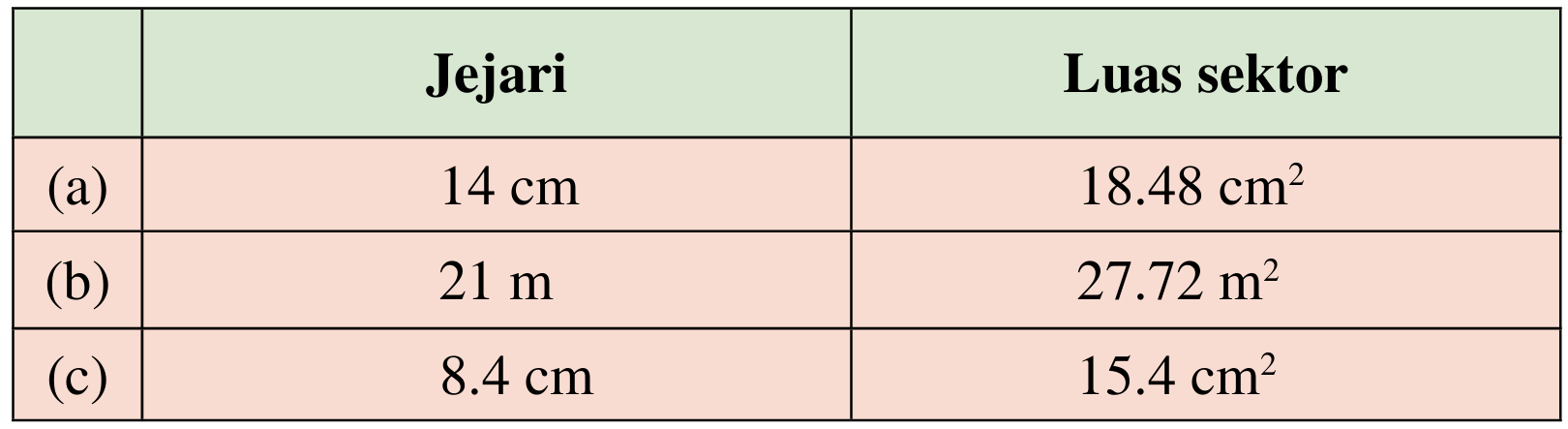
Diberi jejari dan luas sektor bulatan berikut, hitung sudut pada pusat bulatan.
Penyelesaian:
$$ \text { Luas sektor }=\frac{\theta}{360^{\circ}} \times \pi j^2 $$
(a)
$$ \begin{aligned} &\begin{aligned} \frac{\theta}{360^{\circ}} \times \frac{22}{7} \times 14^2 & =18.48 \\ \frac{\theta}{360^{\circ}} & =18.48 \times \frac{7}{22} \times \frac{1}{14 \times 14} \\ \frac{\theta}{360^{\circ}} & =0.03 \\ \theta & =0.03 \times 360^{\circ} \end{aligned}\\ &\text { Sudut pada pusat bulatan, } \theta=10.8^{\circ} \end{aligned} $$
(b)
$$ \begin{aligned} &\begin{aligned} \frac{\theta}{360^{\circ}} \times \frac{22}{7} \times 21^2 & =27.72 \\ \frac{\theta}{360^{\circ}} & =27.72 \times \frac{7}{22} \times \frac{1}{21 \times 21} \\ \frac{\theta}{360^{\circ}} & =0.02 \\ \theta & =0.02 \times 360^{\circ} \end{aligned}\\ &\text { Sudut pada pusat bulatan, } \theta=7.2^{\circ} \end{aligned} $$
(c)
$$ \begin{aligned} &\begin{aligned} \frac{\theta}{360^{\circ}} \times \frac{22}{7} \times 8.4^2 & =15.4 \\ \frac{\theta}{360^{\circ}} & =15.4 \times \frac{7}{22} \times \frac{1}{8.4 \times 8.4} \\ \frac{\theta}{360^{\circ}} & =0.06944 \\ \theta & =0.06944 \times 360^{\circ} \end{aligned}\\ &\text { Sudut pada pusat bulatan, } \theta=25^{\circ} \end{aligned} $$
Diberi jejari dan luas sektor bulatan berikut, hitung sudut pada pusat bulatan.

Penyelesaian:
$$ \text { Luas sektor }=\frac{\theta}{360^{\circ}} \times \pi j^2 $$
(a)
$$ \begin{aligned} &\begin{aligned} \frac{\theta}{360^{\circ}} \times \frac{22}{7} \times 14^2 & =18.48 \\ \frac{\theta}{360^{\circ}} & =18.48 \times \frac{7}{22} \times \frac{1}{14 \times 14} \\ \frac{\theta}{360^{\circ}} & =0.03 \\ \theta & =0.03 \times 360^{\circ} \end{aligned}\\ &\text { Sudut pada pusat bulatan, } \theta=10.8^{\circ} \end{aligned} $$
(b)
$$ \begin{aligned} &\begin{aligned} \frac{\theta}{360^{\circ}} \times \frac{22}{7} \times 21^2 & =27.72 \\ \frac{\theta}{360^{\circ}} & =27.72 \times \frac{7}{22} \times \frac{1}{21 \times 21} \\ \frac{\theta}{360^{\circ}} & =0.02 \\ \theta & =0.02 \times 360^{\circ} \end{aligned}\\ &\text { Sudut pada pusat bulatan, } \theta=7.2^{\circ} \end{aligned} $$
(c)
$$ \begin{aligned} &\begin{aligned} \frac{\theta}{360^{\circ}} \times \frac{22}{7} \times 8.4^2 & =15.4 \\ \frac{\theta}{360^{\circ}} & =15.4 \times \frac{7}{22} \times \frac{1}{8.4 \times 8.4} \\ \frac{\theta}{360^{\circ}} & =0.06944 \\ \theta & =0.06944 \times 360^{\circ} \end{aligned}\\ &\text { Sudut pada pusat bulatan, } \theta=25^{\circ} \end{aligned} $$
Soalan 9:
Rajah di bawah menunjukkan pelan bagi sebuah taman. ABCD ialah sebuah segi empat tepat. APB dan DQC ialah semi bulatan yang masing-masing berpusat di X dan Y. Diberi AB = 7 cm dan AC = 25 cm. Hitung perimeter, dalam cm, taman itu.
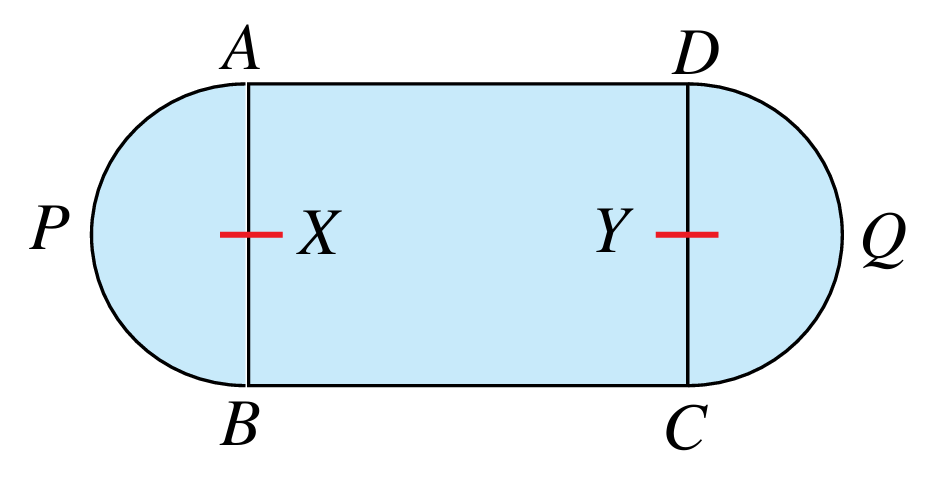
Penyelesaian:
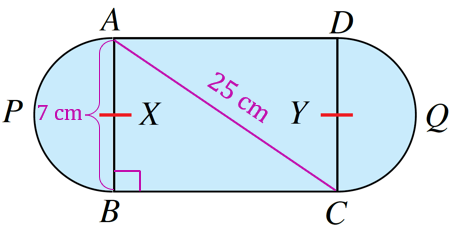
$$ \begin{aligned} \text { Jejari } & =\frac{1}{2} A B \\ & =\frac{1}{2} \times 7 \\ & =3.5 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} &\text { Lengkok } A P B+\text { Lengkok } D Q C=\text { Lilitan bulatan }\\ &\begin{aligned} \text { Lilitan } & =2 \pi j \\ & =2 \times \frac{22}{7} \times 3.5 \\ & =22 \mathrm{~cm} \end{aligned} \end{aligned} $$
△ ABC ialah segi tiga sudut tegak.
$$ \begin{aligned} &\text { Dengan mengguna teorem Pythagores, }\\ &\begin{aligned} B C^2 & =A C^2-A B^2 \\ & =25^2-7^2 \\ & =625-49 \\ & =576 \\ B C & =\sqrt{576} \\ & =24 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Perimeter taman } & =(\text { Lengkok } A P B+\text { Lengkok } D Q C)+A D+B C \\ & =22+24+24 \\ & =70 \mathrm{~cm} \end{aligned} $$
Rajah di bawah menunjukkan pelan bagi sebuah taman. ABCD ialah sebuah segi empat tepat. APB dan DQC ialah semi bulatan yang masing-masing berpusat di X dan Y. Diberi AB = 7 cm dan AC = 25 cm. Hitung perimeter, dalam cm, taman itu.

Penyelesaian:

$$ \begin{aligned} \text { Jejari } & =\frac{1}{2} A B \\ & =\frac{1}{2} \times 7 \\ & =3.5 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} &\text { Lengkok } A P B+\text { Lengkok } D Q C=\text { Lilitan bulatan }\\ &\begin{aligned} \text { Lilitan } & =2 \pi j \\ & =2 \times \frac{22}{7} \times 3.5 \\ & =22 \mathrm{~cm} \end{aligned} \end{aligned} $$
△ ABC ialah segi tiga sudut tegak.
$$ \begin{aligned} &\text { Dengan mengguna teorem Pythagores, }\\ &\begin{aligned} B C^2 & =A C^2-A B^2 \\ & =25^2-7^2 \\ & =625-49 \\ & =576 \\ B C & =\sqrt{576} \\ & =24 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Perimeter taman } & =(\text { Lengkok } A P B+\text { Lengkok } D Q C)+A D+B C \\ & =22+24+24 \\ & =70 \mathrm{~cm} \end{aligned} $$
Soalan 10:
Rajah di bawah menunjukkan sukuan OPQ berpusat O. ORST ialah sebuah segi empat sama. Diberi OP = 10 cm dan OR = 7 cm. Hitung luas, dalam cm2, kawasan yang berlorek. Berikan jawapan dalam π.
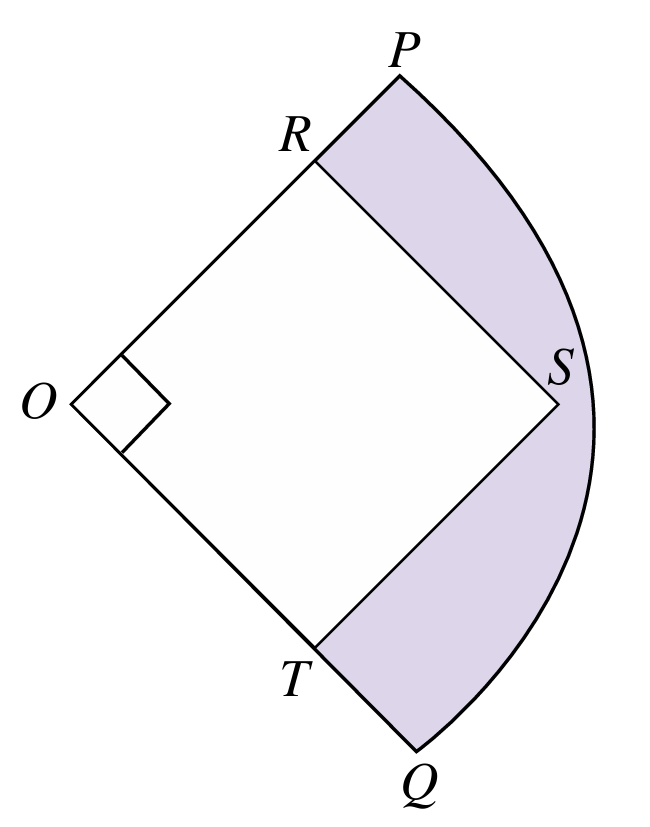
Penyelesaian:
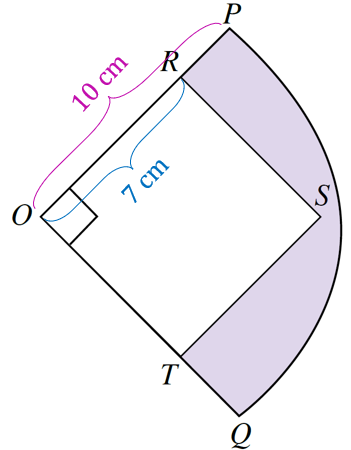
$$ \begin{aligned} & O P=\text { jejari }=10 \mathrm{~cm} \\ & \begin{aligned} \text { Luas sukuan } & =\frac{\theta}{360^{\circ}} \times \pi j^2 \\ & =\frac{90^{\circ}}{360^{\circ}} \times \pi \times 10^2 \\ & =25 \pi \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Luas segi empat sama } & =7 \times 7 \\ & =49 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{aligned} &\text { Luas kawasan yang berlorek }\\ &\begin{aligned} & =\text { Luas sukuan } O P Q-\text { Luas segi empat sama ORST } \\ & =(25 \pi-49) \mathrm{cm}^2 \end{aligned} \end{aligned} $$
Rajah di bawah menunjukkan sukuan OPQ berpusat O. ORST ialah sebuah segi empat sama. Diberi OP = 10 cm dan OR = 7 cm. Hitung luas, dalam cm2, kawasan yang berlorek. Berikan jawapan dalam π.

Penyelesaian:

$$ \begin{aligned} & O P=\text { jejari }=10 \mathrm{~cm} \\ & \begin{aligned} \text { Luas sukuan } & =\frac{\theta}{360^{\circ}} \times \pi j^2 \\ & =\frac{90^{\circ}}{360^{\circ}} \times \pi \times 10^2 \\ & =25 \pi \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Luas segi empat sama } & =7 \times 7 \\ & =49 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{aligned} &\text { Luas kawasan yang berlorek }\\ &\begin{aligned} & =\text { Luas sukuan } O P Q-\text { Luas segi empat sama ORST } \\ & =(25 \pi-49) \mathrm{cm}^2 \end{aligned} \end{aligned} $$