Soalan 5:
Hitung luas bulatan, jika lilitan bulatan ialah 15.4 cm.
Berikan jawapan dalam dua tempat perpuluhan. (Guna π = 22/7 )
Penyelesaian:
$$ \begin{aligned} & \text { Lilitan }=15.4 \mathrm{~cm} \\ & \qquad \begin{aligned} 2 \pi j & =15.4 \\ 2 \times \frac{22}{7} \times j & =15.4 \\ j & =15.4 \times \frac{7}{44} \\ j & =2.45 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Luas } & =\pi j^2 \\ & =\frac{22}{7} \times 2.45^2 \\ & =18.87 \mathrm{~cm}^2 \end{aligned} $$
Hitung luas bulatan, jika lilitan bulatan ialah 15.4 cm.
Berikan jawapan dalam dua tempat perpuluhan. (Guna π = 22/7 )
Penyelesaian:
$$ \begin{aligned} & \text { Lilitan }=15.4 \mathrm{~cm} \\ & \qquad \begin{aligned} 2 \pi j & =15.4 \\ 2 \times \frac{22}{7} \times j & =15.4 \\ j & =15.4 \times \frac{7}{44} \\ j & =2.45 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Luas } & =\pi j^2 \\ & =\frac{22}{7} \times 2.45^2 \\ & =18.87 \mathrm{~cm}^2 \end{aligned} $$
Soalan 6:
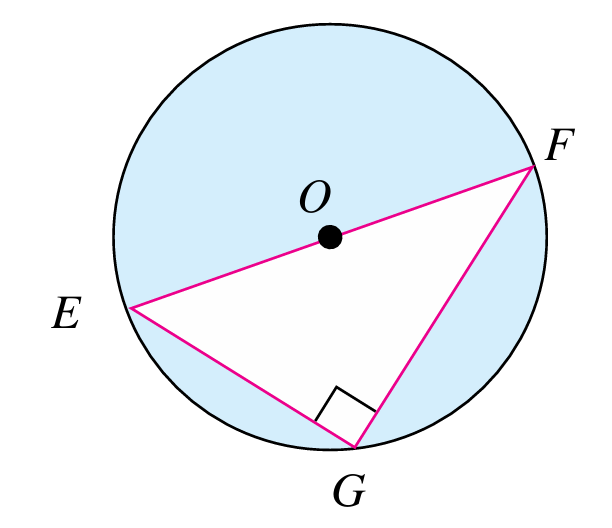
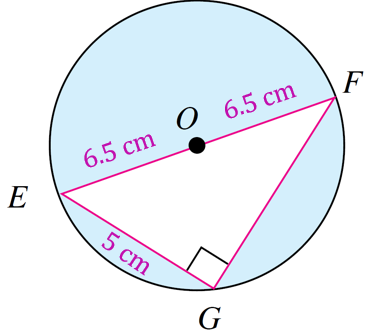
Rajah di bawah menunjukkan sebuah bulatan berpusat O. Diberi OF = 6.5 cm dan EG = 5 cm.
Hitung luas, dalam cm2, kawasan berlorek. Berikan jawapan dalam dua tempat perpuluhan.
(Guna π = 3.142)
Penyelesaian:
$$ \begin{aligned} & O F=O E=\text { jejari }=6.5 \mathrm{~cm} \\ & \begin{aligned} \text { Luas bulatan } & =\pi j^2 \\ & =(3.142)(6.5)^2 \\ & =132.75 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
△ EGF ialah segi tiga sudut tegak.
$$ \begin{aligned} &\text { Dengan mengguna teorem Pythagores, }\\ &\begin{aligned} G F^2 & =E F^2-E G^2 \\ & =(6.5+6.5)^2-5^2 \\ & =13^2-5^2 \\ & =169-25 \\ & =144 \\ G F & =\sqrt{ } 144 \\ G F & =12 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { Luas } \triangle E G F=\frac{1}{2} \times E G \times G F \\ & =\frac{1}{2} \times 5 \times 12 \\ & =30 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{aligned} \text { Luas kawasan berlorek } & =\text { Luas bulatan }- \text { Luas } \triangle E G F \\ & =132.75-30 \\ & =102.75 \mathrm{~cm}^2 \end{aligned} $$
Rajah di bawah menunjukkan sebuah bulatan berpusat O. Diberi OF = 6.5 cm dan EG = 5 cm.
Hitung luas, dalam cm2, kawasan berlorek. Berikan jawapan dalam dua tempat perpuluhan.
(Guna π = 3.142)

Penyelesaian:

$$ \begin{aligned} & O F=O E=\text { jejari }=6.5 \mathrm{~cm} \\ & \begin{aligned} \text { Luas bulatan } & =\pi j^2 \\ & =(3.142)(6.5)^2 \\ & =132.75 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
△ EGF ialah segi tiga sudut tegak.
$$ \begin{aligned} &\text { Dengan mengguna teorem Pythagores, }\\ &\begin{aligned} G F^2 & =E F^2-E G^2 \\ & =(6.5+6.5)^2-5^2 \\ & =13^2-5^2 \\ & =169-25 \\ & =144 \\ G F & =\sqrt{ } 144 \\ G F & =12 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { Luas } \triangle E G F=\frac{1}{2} \times E G \times G F \\ & =\frac{1}{2} \times 5 \times 12 \\ & =30 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{aligned} \text { Luas kawasan berlorek } & =\text { Luas bulatan }- \text { Luas } \triangle E G F \\ & =132.75-30 \\ & =102.75 \mathrm{~cm}^2 \end{aligned} $$
Soalan 7:
Hitung jejari apabila panjang lengkok dan sudut pada pusat bulatan diberi. Nyatakan jawapan dalam dua tempat perpuluhan.

Penyelesaian:
$$ \text { Panjang lengkok }=\frac{\theta}{360^{\circ}} \times 2 \pi j $$
(a)
$$ \begin{aligned} \frac{45^{\circ}}{360^{\circ}} \times(2)\left(\frac{22}{7}\right) j & =11 \\ j & =11 \times 8 \times \frac{1}{2} \times \frac{7}{22} \\ & =14.00 \mathrm{~cm} \end{aligned} $$
(b)
$$ \begin{aligned} \frac{35^{\circ}}{360^{\circ}} \times(2)\left(\frac{22}{7}\right) j & =4.3 \\ j & =4.3 \times \frac{72}{7} \times \frac{1}{2} \times \frac{7}{22} \\ & =7.04 \mathrm{~cm} \end{aligned} $$
(c)
$$ \begin{aligned} \frac{120^{\circ}}{360^{\circ}} \times(2)\left(\frac{22}{7}\right) j & =30.8 \\ j & =30.8 \times 3 \times \frac{1}{2} \times \frac{7}{22} \\ & =14.70 \mathrm{~cm} \end{aligned} $$
(d)
$$ \begin{aligned} \frac{200^{\circ}}{360^{\circ}} \times(2)\left(\frac{22}{7}\right) j & =110 \\ j & =110 \times \frac{9}{5} \times \frac{1}{2} \times \frac{7}{22} \\ & =31.5 \mathrm{~cm} \end{aligned} $$
Hitung jejari apabila panjang lengkok dan sudut pada pusat bulatan diberi. Nyatakan jawapan dalam dua tempat perpuluhan.

Penyelesaian:
$$ \text { Panjang lengkok }=\frac{\theta}{360^{\circ}} \times 2 \pi j $$
(a)
$$ \begin{aligned} \frac{45^{\circ}}{360^{\circ}} \times(2)\left(\frac{22}{7}\right) j & =11 \\ j & =11 \times 8 \times \frac{1}{2} \times \frac{7}{22} \\ & =14.00 \mathrm{~cm} \end{aligned} $$
(b)
$$ \begin{aligned} \frac{35^{\circ}}{360^{\circ}} \times(2)\left(\frac{22}{7}\right) j & =4.3 \\ j & =4.3 \times \frac{72}{7} \times \frac{1}{2} \times \frac{7}{22} \\ & =7.04 \mathrm{~cm} \end{aligned} $$
(c)
$$ \begin{aligned} \frac{120^{\circ}}{360^{\circ}} \times(2)\left(\frac{22}{7}\right) j & =30.8 \\ j & =30.8 \times 3 \times \frac{1}{2} \times \frac{7}{22} \\ & =14.70 \mathrm{~cm} \end{aligned} $$
(d)
$$ \begin{aligned} \frac{200^{\circ}}{360^{\circ}} \times(2)\left(\frac{22}{7}\right) j & =110 \\ j & =110 \times \frac{9}{5} \times \frac{1}{2} \times \frac{7}{22} \\ & =31.5 \mathrm{~cm} \end{aligned} $$