Soalan 9:
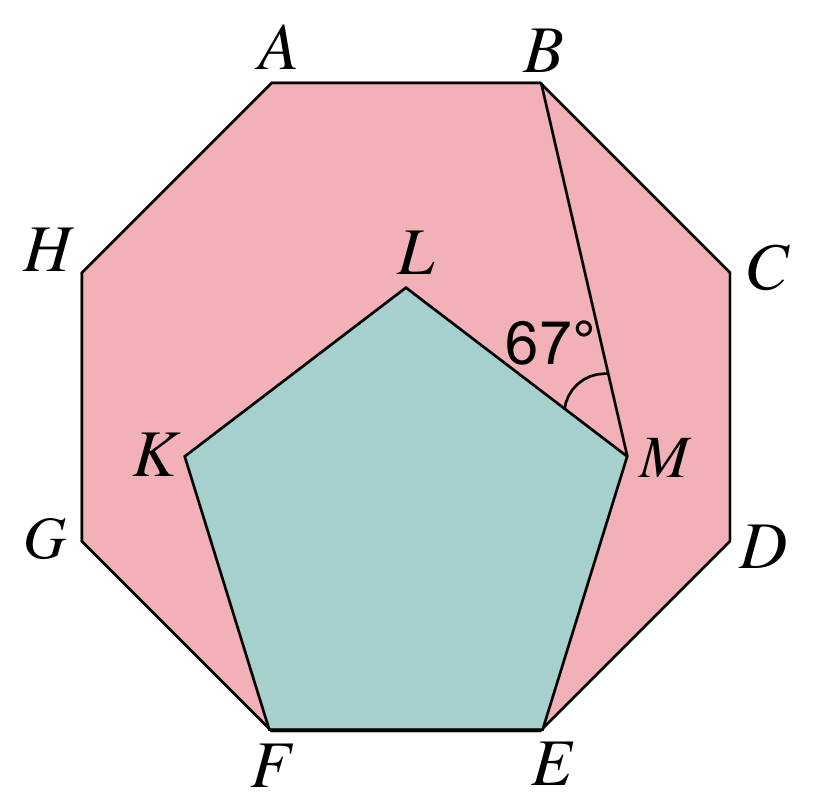
Berdasarkan rajah di bawah, ABCDEFGH ialah sebuah oktagon sekata dan EFKLM ialah sebuah pentagon sekata. Hitung ∠CBM.
Penyelesaian:
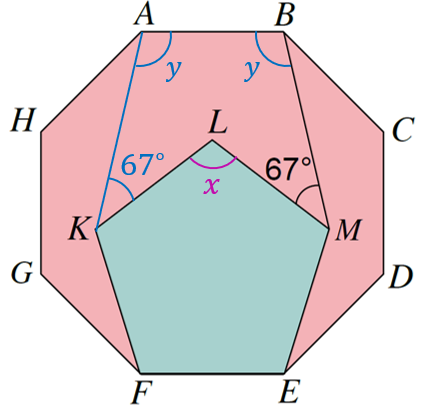
$$ \begin{aligned} &\text { Sudut pedalaman pentagon sekata, }\\ &\begin{aligned} x & =\frac{(n-2) \times 180^{\circ}}{n} \\ & =\frac{(5-2) \times 180^{\circ}}{5} \\ & =\frac{3 \times 180^{\circ}}{5} \\ & =\frac{540^{\circ}}{5} \\ & =108^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Sudut refleks bagi } x\\ &\begin{aligned} & =360^{\circ}-108^{\circ} \\ & =252^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Hasil tambah sudut pedalaman pentagon } A B M L K=540^{\circ}\\ &\begin{aligned} y+y+67^{\circ}+252^{\circ}+67^{\circ} & =540^{\circ} \\ 2 y+386^{\circ} & =540^{\circ} \\ 2 y & =154^{\circ} \\ y & =\frac{154^{\circ}}{2} \\ y & =77^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Sudut pedalaman oktagon sekata }\\ &\begin{aligned} & =\frac{(8-2) \times 180^{\circ}}{8} \\ & =\frac{6 \times 180^{\circ}}{8} \\ & =\frac{1080^{\circ}}{8} \\ & =135^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \therefore \angle C B M+y & =135^{\circ} \\ \angle C B M & =135^{\circ}-77^{\circ} \\ & =58^{\circ} \end{aligned} $$
Berdasarkan rajah di bawah, ABCDEFGH ialah sebuah oktagon sekata dan EFKLM ialah sebuah pentagon sekata. Hitung ∠CBM.

Penyelesaian:

$$ \begin{aligned} &\text { Sudut pedalaman pentagon sekata, }\\ &\begin{aligned} x & =\frac{(n-2) \times 180^{\circ}}{n} \\ & =\frac{(5-2) \times 180^{\circ}}{5} \\ & =\frac{3 \times 180^{\circ}}{5} \\ & =\frac{540^{\circ}}{5} \\ & =108^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Sudut refleks bagi } x\\ &\begin{aligned} & =360^{\circ}-108^{\circ} \\ & =252^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Hasil tambah sudut pedalaman pentagon } A B M L K=540^{\circ}\\ &\begin{aligned} y+y+67^{\circ}+252^{\circ}+67^{\circ} & =540^{\circ} \\ 2 y+386^{\circ} & =540^{\circ} \\ 2 y & =154^{\circ} \\ y & =\frac{154^{\circ}}{2} \\ y & =77^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Sudut pedalaman oktagon sekata }\\ &\begin{aligned} & =\frac{(8-2) \times 180^{\circ}}{8} \\ & =\frac{6 \times 180^{\circ}}{8} \\ & =\frac{1080^{\circ}}{8} \\ & =135^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \therefore \angle C B M+y & =135^{\circ} \\ \angle C B M & =135^{\circ}-77^{\circ} \\ & =58^{\circ} \end{aligned} $$
Soalan 10:
Sudut peluaran sebuah poligon sekata ialah 2h, manakala sudut pedalaman poligon yang sama ialah 7h.
(a) Hitung nilai h.
(b) Hitung sudut pedalaman dan sudut peluarannya.
(c) Hitung bilangan sisi poligon dan namakan poligon tersebut.
Penyelesaian:
(a)
$$ \begin{aligned} \text { Sudut peluaran + sudut pedalaman } & =180^{\circ} \\ 2 h+7 h & =180^{\circ} \\ 9 h & =180^{\circ} \\ h & =\frac{180^{\circ}}{9} \\ h & =20^{\circ} \end{aligned} $$
(b)
$$ \begin{aligned} \text { Sudut peluaran } & =2 h \\ & =2 \times 20^{\circ} \\ & =40^{\circ} \end{aligned} $$
$$ \begin{aligned} \text { Sudut pedalaman } & =7 \mathrm{~h} \\ & =7 \times 20^{\circ} \\ & =140^{\circ} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Bilangan sisi, } n\\ &\begin{aligned} & =\frac{360^{\circ}}{\text { Sudut peluaran }} \\ & =\frac{360^{\circ}}{40^{\circ}} \\ & =9=\text { nonagon } \end{aligned} \end{aligned} $$
Sudut peluaran sebuah poligon sekata ialah 2h, manakala sudut pedalaman poligon yang sama ialah 7h.
(a) Hitung nilai h.
(b) Hitung sudut pedalaman dan sudut peluarannya.
(c) Hitung bilangan sisi poligon dan namakan poligon tersebut.
Penyelesaian:
(a)
$$ \begin{aligned} \text { Sudut peluaran + sudut pedalaman } & =180^{\circ} \\ 2 h+7 h & =180^{\circ} \\ 9 h & =180^{\circ} \\ h & =\frac{180^{\circ}}{9} \\ h & =20^{\circ} \end{aligned} $$
(b)
$$ \begin{aligned} \text { Sudut peluaran } & =2 h \\ & =2 \times 20^{\circ} \\ & =40^{\circ} \end{aligned} $$
$$ \begin{aligned} \text { Sudut pedalaman } & =7 \mathrm{~h} \\ & =7 \times 20^{\circ} \\ & =140^{\circ} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Bilangan sisi, } n\\ &\begin{aligned} & =\frac{360^{\circ}}{\text { Sudut peluaran }} \\ & =\frac{360^{\circ}}{40^{\circ}} \\ & =9=\text { nonagon } \end{aligned} \end{aligned} $$
Soalan 11:
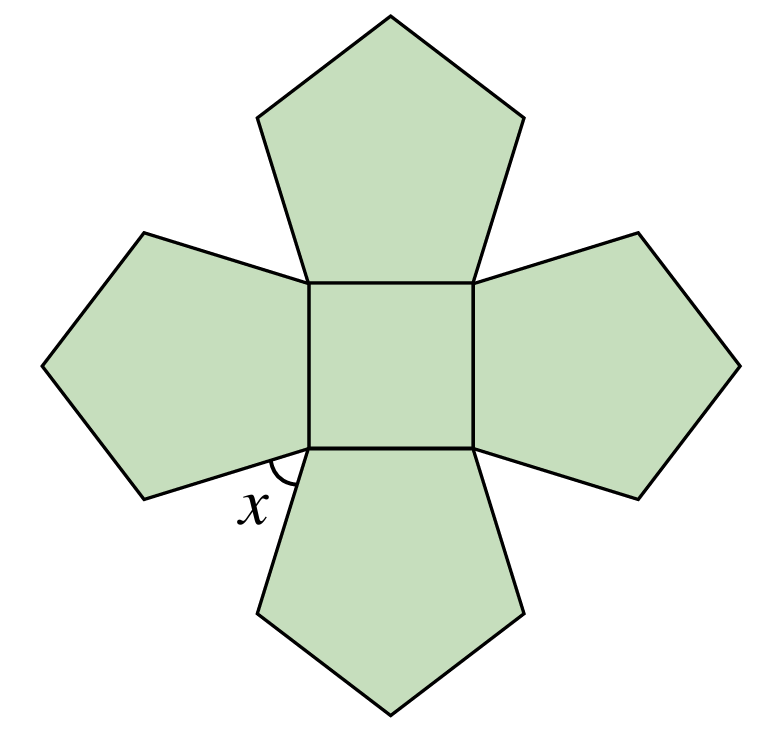
Rajah di bawah ialah 4 buah pentagon sekata dan sebuah segi empat sama. Hitung nilai x.
Penyelesaian:
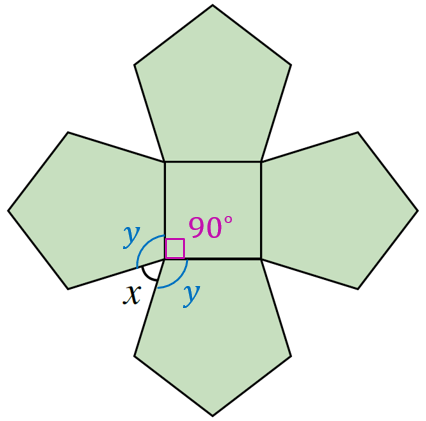
$$ \text { Sudut pedalaman segi empat sama }=90^{\circ} $$
$$ \begin{aligned} &\text { Sudut pedalaman pentagon sekata, }\\ &\begin{aligned} y & =\frac{(n-2) \times 180^{\circ}}{n} \\ & =\frac{(5-2) \times 180^{\circ}}{5} \\ & =\frac{3 \times 180^{\circ}}{5} \\ & =\frac{540^{\circ}}{5} \\ & =108^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} x+y+y+90^{\circ} & =360^{\circ} \\ x+108^{\circ}+108^{\circ}+90^{\circ} & =360^{\circ} \\ x+306^{\circ} & =360^{\circ} \\ x & =360^{\circ}-306^{\circ} \\ x & =54^{\circ} \end{aligned} $$
Rajah di bawah ialah 4 buah pentagon sekata dan sebuah segi empat sama. Hitung nilai x.

Penyelesaian:

$$ \text { Sudut pedalaman segi empat sama }=90^{\circ} $$
$$ \begin{aligned} &\text { Sudut pedalaman pentagon sekata, }\\ &\begin{aligned} y & =\frac{(n-2) \times 180^{\circ}}{n} \\ & =\frac{(5-2) \times 180^{\circ}}{5} \\ & =\frac{3 \times 180^{\circ}}{5} \\ & =\frac{540^{\circ}}{5} \\ & =108^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} x+y+y+90^{\circ} & =360^{\circ} \\ x+108^{\circ}+108^{\circ}+90^{\circ} & =360^{\circ} \\ x+306^{\circ} & =360^{\circ} \\ x & =360^{\circ}-306^{\circ} \\ x & =54^{\circ} \end{aligned} $$