Soalan 12:
Bahar ingin membina sebuah poligon yang mempunyai jumlah sudut pedalaman 300°. Bolehkah Bahar membina poligon tersebut? Jelaskan jawapan anda.
Penyelesaian:
$$ \begin{aligned} \text { Sudut pedalaman poligon } & =\frac{(n-2) \times 180^{\circ}}{n} \\ 300^{\circ} & =\frac{(n-2) \times 180^{\circ}}{n} \\ 300^{\circ} n & =180^{\circ} n-360^{\circ} \\ 300^{\circ} n-180^{\circ} n & =-360^{\circ} \\ 120^{\circ} n & =-360^{\circ} \\ n & =-\frac{360^{\circ}}{120^{\circ}} \\ n & =-3 \end{aligned} $$
Bahar tidak dapat membina poligon tersebut sebab n tidak mungkin nilai negatif.
Bahar ingin membina sebuah poligon yang mempunyai jumlah sudut pedalaman 300°. Bolehkah Bahar membina poligon tersebut? Jelaskan jawapan anda.
Penyelesaian:
$$ \begin{aligned} \text { Sudut pedalaman poligon } & =\frac{(n-2) \times 180^{\circ}}{n} \\ 300^{\circ} & =\frac{(n-2) \times 180^{\circ}}{n} \\ 300^{\circ} n & =180^{\circ} n-360^{\circ} \\ 300^{\circ} n-180^{\circ} n & =-360^{\circ} \\ 120^{\circ} n & =-360^{\circ} \\ n & =-\frac{360^{\circ}}{120^{\circ}} \\ n & =-3 \end{aligned} $$
Bahar tidak dapat membina poligon tersebut sebab n tidak mungkin nilai negatif.
Soalan 13:
Rajah di bawah menunjukkan sebahagian daripada corak yang terhasil melalui cantuman jubin. Terdapat dua jenis jubin, iaitu jubin A dan jubin B yang merupakan poligon sekata. Hitung bilangan sisi jubin A.
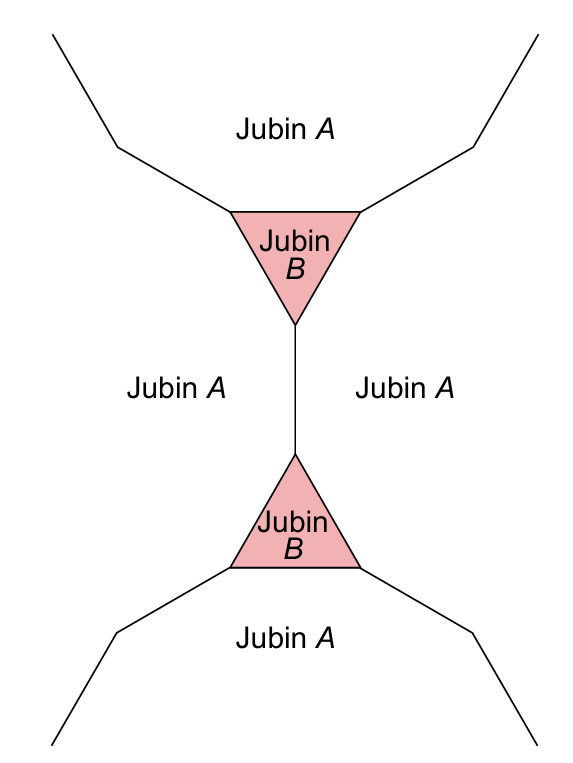
Penyelesaian:
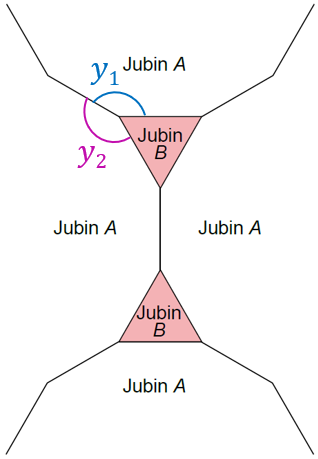
Jubin B ialah segi tiga sama sisi, maka sudut pedalamannya ialah 60∘
$$ \begin{aligned} \angle y_1 & =\angle y_2 \\ \angle y_1+\angle y_2+60^{\circ} & =360^{\circ} \\ 2 y & =360^{\circ}-60^{\circ} \\ y & =\frac{300^{\circ}}{2} \\ y & =150^{\circ} \end{aligned} $$
$$ \begin{aligned} \text { Sudut pedalaman poligon sekata } & =\frac{(n-2) \times 180^{\circ}}{n} \\ 150^{\circ} & =\frac{(n-2)\left(180^{\circ}\right)}{n} \\ 150^{\circ} n & =180^{\circ} n-360^{\circ} \\ 180^{\circ} n-150^{\circ} n & =360^{\circ} \\ n & =\frac{360^{\circ}}{30^{\circ}} \\ n & =12(\text { Bilangan sisi jubin } A) \end{aligned} $$
Rajah di bawah menunjukkan sebahagian daripada corak yang terhasil melalui cantuman jubin. Terdapat dua jenis jubin, iaitu jubin A dan jubin B yang merupakan poligon sekata. Hitung bilangan sisi jubin A.

Penyelesaian:

Jubin B ialah segi tiga sama sisi, maka sudut pedalamannya ialah 60∘
$$ \begin{aligned} \angle y_1 & =\angle y_2 \\ \angle y_1+\angle y_2+60^{\circ} & =360^{\circ} \\ 2 y & =360^{\circ}-60^{\circ} \\ y & =\frac{300^{\circ}}{2} \\ y & =150^{\circ} \end{aligned} $$
$$ \begin{aligned} \text { Sudut pedalaman poligon sekata } & =\frac{(n-2) \times 180^{\circ}}{n} \\ 150^{\circ} & =\frac{(n-2)\left(180^{\circ}\right)}{n} \\ 150^{\circ} n & =180^{\circ} n-360^{\circ} \\ 180^{\circ} n-150^{\circ} n & =360^{\circ} \\ n & =\frac{360^{\circ}}{30^{\circ}} \\ n & =12(\text { Bilangan sisi jubin } A) \end{aligned} $$
Soalan 14:
Devaa adalah seorang pelajar jurusan reka grafik di sebuah universiti tempatan. Bantu Devaa menghitung nilai x untuk membina bingkai gambar bercirikan gabungan poligon yang terdiri daripada sebuah pentagon sekata dan dua buah rombus.
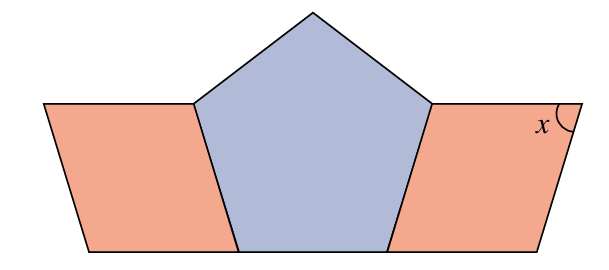
Penyelesaian:
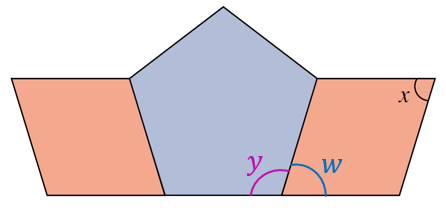
$$ \begin{aligned} &\text { Sudut pedalaman pentagon sekata, }\\ &\begin{aligned} y & =\frac{(5-2) \times 180^{\circ}}{5} \\ & =\frac{3 \times 180^{\circ}}{5} \\ & =\frac{540^{\circ}}{5} \\ & =108^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} y+w & =180^{\circ} \\ 108^{\circ}+w & =180^{\circ} \\ w & =180^{\circ}-108^{\circ} \\ w & =72^{\circ} \end{aligned} $$
$$ \begin{aligned} \text { Sudut bertentangan dalam rombus adalah sama, } x & =w \\ \text { Maka, } x & =72^{\circ} \end{aligned} $$
Devaa adalah seorang pelajar jurusan reka grafik di sebuah universiti tempatan. Bantu Devaa menghitung nilai x untuk membina bingkai gambar bercirikan gabungan poligon yang terdiri daripada sebuah pentagon sekata dan dua buah rombus.

Penyelesaian:

$$ \begin{aligned} &\text { Sudut pedalaman pentagon sekata, }\\ &\begin{aligned} y & =\frac{(5-2) \times 180^{\circ}}{5} \\ & =\frac{3 \times 180^{\circ}}{5} \\ & =\frac{540^{\circ}}{5} \\ & =108^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} y+w & =180^{\circ} \\ 108^{\circ}+w & =180^{\circ} \\ w & =180^{\circ}-108^{\circ} \\ w & =72^{\circ} \end{aligned} $$
$$ \begin{aligned} \text { Sudut bertentangan dalam rombus adalah sama, } x & =w \\ \text { Maka, } x & =72^{\circ} \end{aligned} $$
Soalan 15:
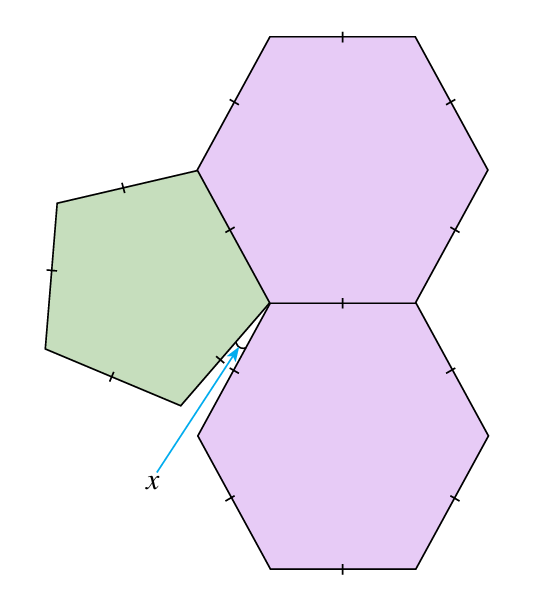
Hitung nilai x.
Penyelesaian:
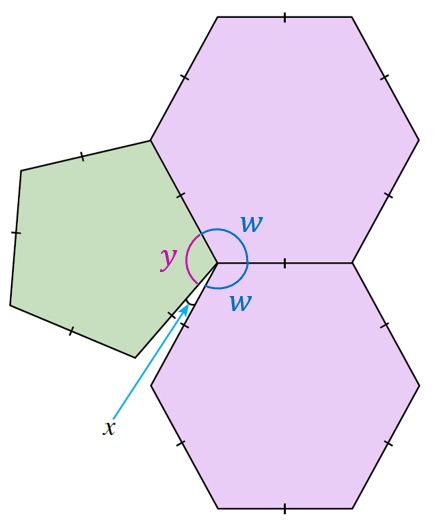
$$ \begin{aligned} &\text { Sudut pedalaman pentagon sekata, }\\ &\begin{aligned} y & =\frac{(5-2) \times 180^{\circ}}{5} \\ & =\frac{3 \times 180^{\circ}}{5} \\ & =\frac{540^{\circ}}{5} \\ & =108^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Sudut pedalaman heksagon sekata, }\\ &\begin{aligned} w & =\frac{(6-2) \times 180^{\circ}}{6} \\ & =\frac{4 \times 180^{\circ}}{6} \\ & =\frac{720^{\circ}}{6} \\ & =120^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} x+w+w+y & =360^{\circ} \\ x+120^{\circ}+120^{\circ}+108^{\circ} & =360^{\circ} \\ x+348^{\circ} & =360^{\circ} \\ x & =360^{\circ}-348^{\circ} \\ x & =12^{\circ} \end{aligned} $$
Hitung nilai x.

Penyelesaian:

$$ \begin{aligned} &\text { Sudut pedalaman pentagon sekata, }\\ &\begin{aligned} y & =\frac{(5-2) \times 180^{\circ}}{5} \\ & =\frac{3 \times 180^{\circ}}{5} \\ & =\frac{540^{\circ}}{5} \\ & =108^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Sudut pedalaman heksagon sekata, }\\ &\begin{aligned} w & =\frac{(6-2) \times 180^{\circ}}{6} \\ & =\frac{4 \times 180^{\circ}}{6} \\ & =\frac{720^{\circ}}{6} \\ & =120^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} x+w+w+y & =360^{\circ} \\ x+120^{\circ}+120^{\circ}+108^{\circ} & =360^{\circ} \\ x+348^{\circ} & =360^{\circ} \\ x & =360^{\circ}-348^{\circ} \\ x & =12^{\circ} \end{aligned} $$