Soalan 1:
Ungkapkan huruf dalam kurungan sebagai perkara rumus.
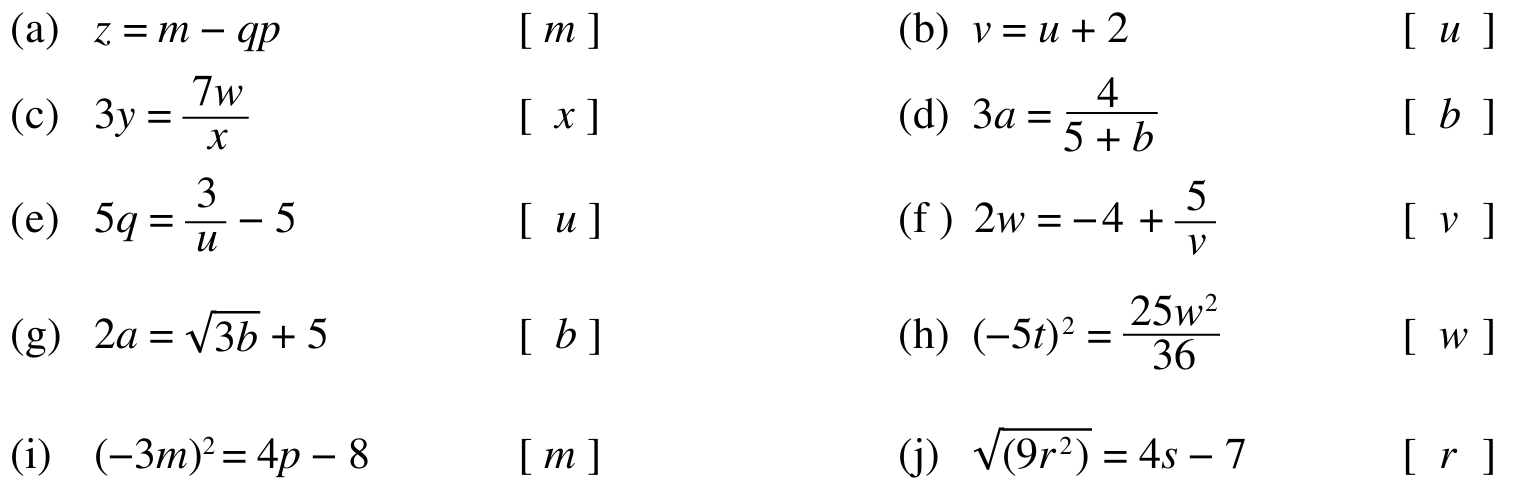
Penyelesaian:
(a)
$$ \begin{aligned} z & =m-q p \\ z+q p & =m-q p+q p \\ z+q p & =m \\ m & =z+q p \end{aligned} $$
(b)
$$ \begin{aligned} v & =u+2 \\ v-2 & =u+2-2 \\ v-2 & =u \\ u & =v-2 \end{aligned} $$
(c)
$$ \begin{aligned} 3 y & =\frac{7 w}{x} \\ 3 y(x) & =\frac{7 w}{x}(x) \\ 3 x y & =7 w \\ 3 x y\left(\frac{1}{3 y}\right) & =7 w\left(\frac{1}{3 y}\right) \\ x & =\frac{7 w}{3 y} \end{aligned} $$
(d)
$$ \begin{aligned} 3 a & =\frac{4}{5+b} \\ 3 a(5+b) & =\frac{4}{5+b}(5+b) \\ 3 a(5+b) & =4 \\ 15 a+3 a b & =4 \\ 15 a+3 a b-15 a & =4-15 a \\ 3 a b & =4-15 a \\ 3 a b\left(\frac{1}{3 a}\right) & =(4-15 a)\left(\frac{1}{3 a}\right) \\ b & =\frac{4-15 a}{3 a} \\ & =\frac{4}{3 a}-\frac{15 a}{3 a} \\ b & =\frac{4}{3 a}-5 \end{aligned} $$
(e)
$$ \begin{aligned} 5 q & =\frac{3}{u}-5 \\ 5 q+5 & =\frac{3}{u}-5+5 \\ 5 q+5 & =\frac{3}{u} \\ (5 q+5)(u) & =\frac{3}{u}(u) \\ u(5 q+5) & =3 \\ u(5 q+5)\left(\frac{1}{5 q+5}\right) & =3\left(\frac{1}{5 q+5}\right) \\ u & =\frac{3}{5 q+5} \end{aligned} $$
(f)
$$ \begin{aligned} 2 w & =-4+\frac{5}{v} \\ 2 w+4 & =-4+\frac{5}{v}+4 \\ 2 w+4 & =\frac{5}{v} \\ (2 w+4)(v) & =\frac{5}{v}(v) \\ v(2 w+4) & =5 \\ v(2 w+4)\left(\frac{1}{2 w+4}\right) & =5\left(\frac{1}{2 w+4}\right) \\ v & =\frac{5}{2 w+4} \end{aligned} $$
(g)
$$ \begin{aligned} 2 a & =\sqrt{3 b}+5 \\ 2 a-5 & =\sqrt{3 b}+5-5 \\ 2 a-5 & =\sqrt{3 b} \\ (2 a-5)^2 & =(\sqrt{3 b})^2 \\ (2 a-5)^2 & =3 b \\ (2 a-5)^2\left(\frac{1}{3}\right) & =3 b\left(\frac{1}{3}\right) \\ \frac{(2 a-5)^2}{3} & =b \\ b & =\frac{(2 a-5)^2}{3} \end{aligned} $$
(h)
$$ \begin{aligned} (-5 t)^2 & =\frac{25 w^2}{36} \\ \left(25 t^2\right)(36) & =\frac{25 w^2}{36}(36) \\ \left(25 t^2\right)(36) & =25 w^2 \\ \left(25 t^2\right)(36)\left(\frac{1}{25}\right) & =25 w^2\left(\frac{1}{25}\right) \\ 36 t^2 & =w^2 \\ \sqrt{36 t^2} & =\sqrt{w^2} \longleftrightarrow \quad \text { Kedua-dua belah persamaan } \\ \sqrt{(6 t)^2} & =\sqrt{w^2} \quad \text { dipuncakuasaduakan } \\ 6 t & =w \\ w & =6 t \end{aligned} $$
(i)
$$ \begin{aligned} (-3 m)^2 & =4 p-8 \\ \sqrt{(-3 m)^2} & =\sqrt{4 p-8} \\ -3 m & =\sqrt{4 p-8} \\ (-3 m)\left(-\frac{1}{3}\right) & =\sqrt{4 p-8}\left(-\frac{1}{3}\right) \\ m & =-\frac{\sqrt{4 p-8}}{3} \end{aligned} $$
(j)
$$ \begin{aligned} \sqrt{\left(9 r^2\right)} & =4 s-7 \\ \sqrt{(3 r)^2} & =4 s-7 \\ 3 r & =4 s-7 \\ (3 r)\left(\frac{1}{3}\right) & =(4 s-7)\left(\frac{1}{3}\right) \\ r & =\frac{4 s-7}{3} \end{aligned} $$
Ungkapkan huruf dalam kurungan sebagai perkara rumus.
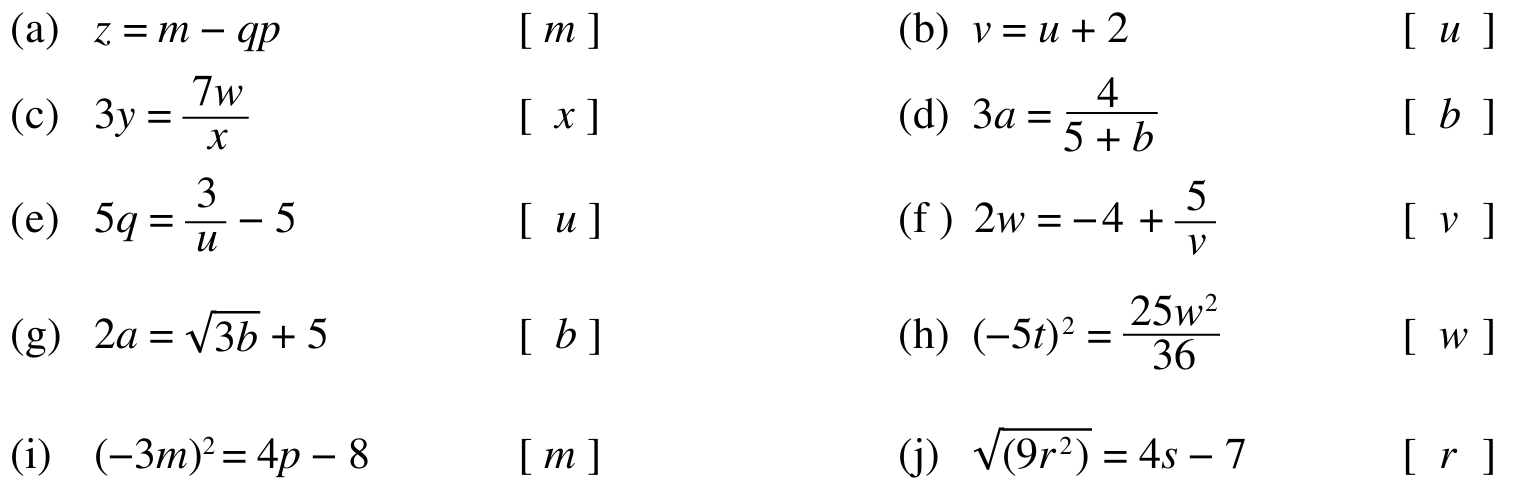
Penyelesaian:
(a)
$$ \begin{aligned} z & =m-q p \\ z+q p & =m-q p+q p \\ z+q p & =m \\ m & =z+q p \end{aligned} $$
(b)
$$ \begin{aligned} v & =u+2 \\ v-2 & =u+2-2 \\ v-2 & =u \\ u & =v-2 \end{aligned} $$
(c)
$$ \begin{aligned} 3 y & =\frac{7 w}{x} \\ 3 y(x) & =\frac{7 w}{x}(x) \\ 3 x y & =7 w \\ 3 x y\left(\frac{1}{3 y}\right) & =7 w\left(\frac{1}{3 y}\right) \\ x & =\frac{7 w}{3 y} \end{aligned} $$
(d)
$$ \begin{aligned} 3 a & =\frac{4}{5+b} \\ 3 a(5+b) & =\frac{4}{5+b}(5+b) \\ 3 a(5+b) & =4 \\ 15 a+3 a b & =4 \\ 15 a+3 a b-15 a & =4-15 a \\ 3 a b & =4-15 a \\ 3 a b\left(\frac{1}{3 a}\right) & =(4-15 a)\left(\frac{1}{3 a}\right) \\ b & =\frac{4-15 a}{3 a} \\ & =\frac{4}{3 a}-\frac{15 a}{3 a} \\ b & =\frac{4}{3 a}-5 \end{aligned} $$
(e)
$$ \begin{aligned} 5 q & =\frac{3}{u}-5 \\ 5 q+5 & =\frac{3}{u}-5+5 \\ 5 q+5 & =\frac{3}{u} \\ (5 q+5)(u) & =\frac{3}{u}(u) \\ u(5 q+5) & =3 \\ u(5 q+5)\left(\frac{1}{5 q+5}\right) & =3\left(\frac{1}{5 q+5}\right) \\ u & =\frac{3}{5 q+5} \end{aligned} $$
(f)
$$ \begin{aligned} 2 w & =-4+\frac{5}{v} \\ 2 w+4 & =-4+\frac{5}{v}+4 \\ 2 w+4 & =\frac{5}{v} \\ (2 w+4)(v) & =\frac{5}{v}(v) \\ v(2 w+4) & =5 \\ v(2 w+4)\left(\frac{1}{2 w+4}\right) & =5\left(\frac{1}{2 w+4}\right) \\ v & =\frac{5}{2 w+4} \end{aligned} $$
(g)
$$ \begin{aligned} 2 a & =\sqrt{3 b}+5 \\ 2 a-5 & =\sqrt{3 b}+5-5 \\ 2 a-5 & =\sqrt{3 b} \\ (2 a-5)^2 & =(\sqrt{3 b})^2 \\ (2 a-5)^2 & =3 b \\ (2 a-5)^2\left(\frac{1}{3}\right) & =3 b\left(\frac{1}{3}\right) \\ \frac{(2 a-5)^2}{3} & =b \\ b & =\frac{(2 a-5)^2}{3} \end{aligned} $$
(h)
$$ \begin{aligned} (-5 t)^2 & =\frac{25 w^2}{36} \\ \left(25 t^2\right)(36) & =\frac{25 w^2}{36}(36) \\ \left(25 t^2\right)(36) & =25 w^2 \\ \left(25 t^2\right)(36)\left(\frac{1}{25}\right) & =25 w^2\left(\frac{1}{25}\right) \\ 36 t^2 & =w^2 \\ \sqrt{36 t^2} & =\sqrt{w^2} \longleftrightarrow \quad \text { Kedua-dua belah persamaan } \\ \sqrt{(6 t)^2} & =\sqrt{w^2} \quad \text { dipuncakuasaduakan } \\ 6 t & =w \\ w & =6 t \end{aligned} $$
(i)
$$ \begin{aligned} (-3 m)^2 & =4 p-8 \\ \sqrt{(-3 m)^2} & =\sqrt{4 p-8} \\ -3 m & =\sqrt{4 p-8} \\ (-3 m)\left(-\frac{1}{3}\right) & =\sqrt{4 p-8}\left(-\frac{1}{3}\right) \\ m & =-\frac{\sqrt{4 p-8}}{3} \end{aligned} $$
(j)
$$ \begin{aligned} \sqrt{\left(9 r^2\right)} & =4 s-7 \\ \sqrt{(3 r)^2} & =4 s-7 \\ 3 r & =4 s-7 \\ (3 r)\left(\frac{1}{3}\right) & =(4 s-7)\left(\frac{1}{3}\right) \\ r & =\frac{4 s-7}{3} \end{aligned} $$
Soalan 2:
Harga sehelai kemeja ialah RM35, manakala harga sehelai seluar ialah RM45. Diskaun sebanyak 15% diberikan pada harga sehelai kemeja, manakala diskaun sebanyak 10% diberikan pada harga sehelai seluar. Tulis rumus jualan, z, jika Syamsul ingin membeli x helai kemeja dan y helai seluar.
Penyelesaian:
$$ \begin{aligned} &\text { Harga sehelai kemeja selepas diskaun }\\ &\begin{aligned} & =\text { RM35 } \times 85 \% \\ & =\text { RM35 } \times \frac{85}{100} \\ & =\text { RM29.75 } \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Harga sehelai seluar selepas diskaun }\\ &\begin{aligned} & =\mathrm{RM} 45 \times 90 \% \\ & =\text { RM45 } \times \frac{90}{100} \\ & =\text { RM40.50 } \end{aligned} \end{aligned} $$
Maka, kos untuk membeli x helai kemeja dan y helai seluar,
z = 29.75x + 40.50y
Harga sehelai kemeja ialah RM35, manakala harga sehelai seluar ialah RM45. Diskaun sebanyak 15% diberikan pada harga sehelai kemeja, manakala diskaun sebanyak 10% diberikan pada harga sehelai seluar. Tulis rumus jualan, z, jika Syamsul ingin membeli x helai kemeja dan y helai seluar.
Penyelesaian:
$$ \begin{aligned} &\text { Harga sehelai kemeja selepas diskaun }\\ &\begin{aligned} & =\text { RM35 } \times 85 \% \\ & =\text { RM35 } \times \frac{85}{100} \\ & =\text { RM29.75 } \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Harga sehelai seluar selepas diskaun }\\ &\begin{aligned} & =\mathrm{RM} 45 \times 90 \% \\ & =\text { RM45 } \times \frac{90}{100} \\ & =\text { RM40.50 } \end{aligned} \end{aligned} $$
Maka, kos untuk membeli x helai kemeja dan y helai seluar,
z = 29.75x + 40.50y