Soalan 1:
Hitung nilai sin θ, kos θ dan tan θ bagi setiap segi tiga bersudut tegak berikut.
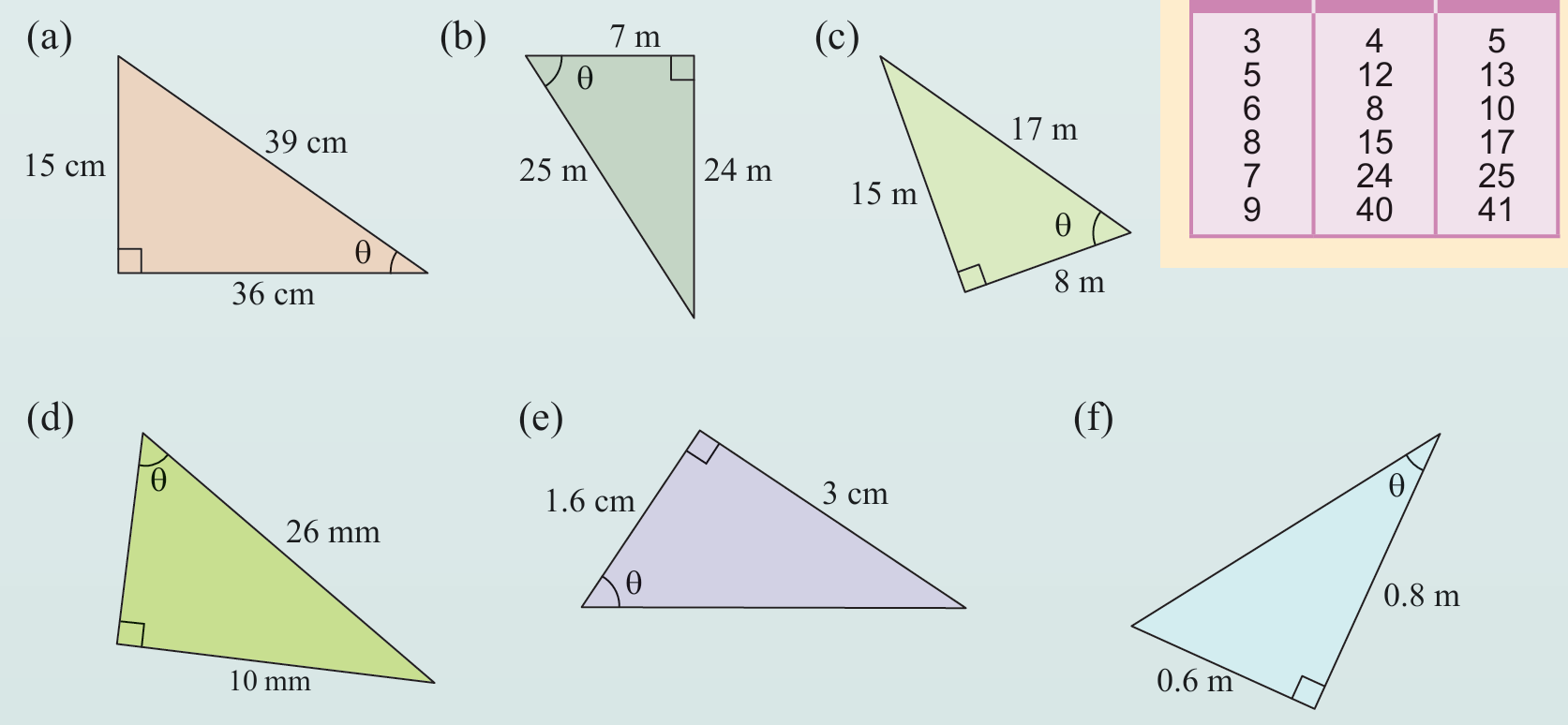
Penyelesaian:
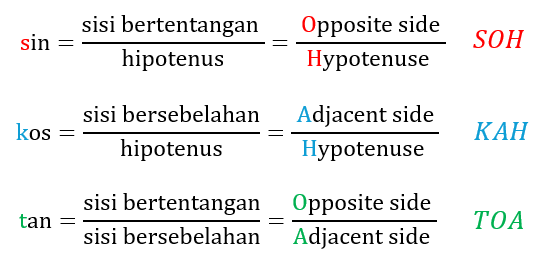
(a)
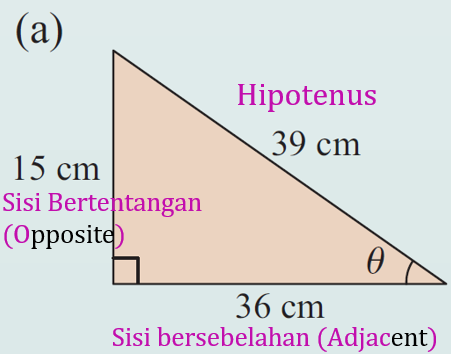

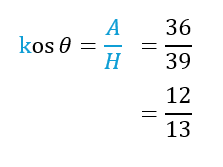
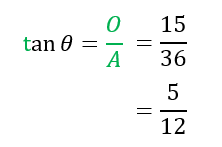
(b)
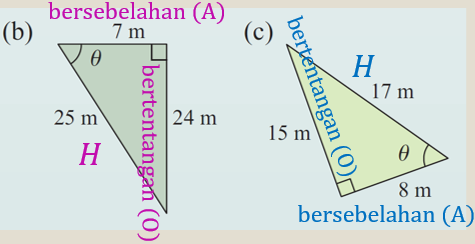
$$ \sin \theta=\frac{O}{H}=\frac{24}{25} $$
$$ \operatorname{kos} \theta=\frac{A}{H}=\frac{7}{25} $$
$$ \tan \theta=\frac{O}{A}=\frac{24}{7} $$
(c)
$$ \sin \theta=\frac{O}{H}=\frac{15}{17} $$
$$ \operatorname{kos} \theta=\frac{A}{H}=\frac{8}{17} $$
$$ \tan \theta=\frac{O}{A}=\frac{15}{8} $$
(d)
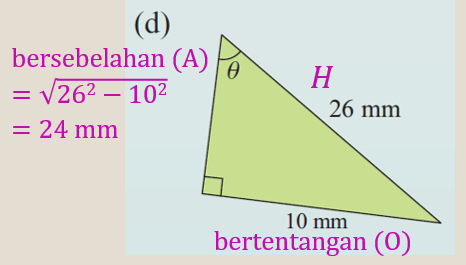
$$ \begin{aligned} \sin \theta & =\frac{O}{H} \\ & =\frac{10}{26} \\ & =\frac{5}{13} \end{aligned} $$
$$ \begin{aligned} \operatorname{kos} \theta & =\frac{A}{H} \\ & =\frac{24}{26} \\ & =\frac{12}{13} \end{aligned} $$
$$ \begin{aligned} \tan \theta & =\frac{O}{A} \\ & =\frac{10}{24} \\ & =\frac{5}{12} \end{aligned} $$
(e)
$$ \begin{aligned} \sin \theta & =\frac{O}{H} \\ & =\frac{3}{3.4} \\ & =\frac{15}{17} \end{aligned} $$
$$ \begin{aligned} \operatorname{kos} \theta & =\frac{A}{H} \\ & =\frac{1.6}{3.4} \\ & =\frac{8}{17} \end{aligned} $$
$$ \begin{aligned} \tan \theta & =\frac{O}{A} \\ & =\frac{3}{1.6} \\ & =\frac{15}{8} \end{aligned} $$
(f)
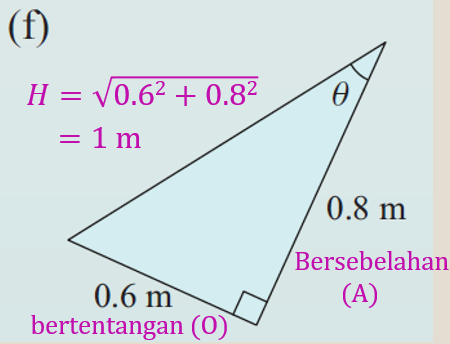
$$ \begin{aligned} \sin \theta & =\frac{O}{H} \\ & =\frac{0.6}{1} \\ & =\frac{6}{10} \\ & =\frac{3}{5} \end{aligned} $$
$$ \begin{aligned} \operatorname{kos} \theta & =\frac{A}{H} \\ & =\frac{0.8}{1} \\ & =\frac{8}{10} \\ & =\frac{4}{5} \end{aligned} $$
$$ \begin{aligned} \tan \theta & =\frac{O}{A} \\ & =\frac{0.6}{0.8} \\ & =\frac{3}{4} \end{aligned} $$
Hitung nilai sin θ, kos θ dan tan θ bagi setiap segi tiga bersudut tegak berikut.

Penyelesaian:

(a)


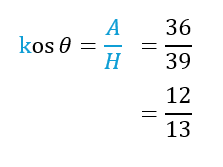
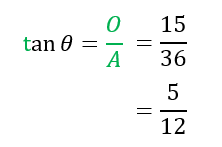
(b)

$$ \sin \theta=\frac{O}{H}=\frac{24}{25} $$
$$ \operatorname{kos} \theta=\frac{A}{H}=\frac{7}{25} $$
$$ \tan \theta=\frac{O}{A}=\frac{24}{7} $$
(c)
$$ \sin \theta=\frac{O}{H}=\frac{15}{17} $$
$$ \operatorname{kos} \theta=\frac{A}{H}=\frac{8}{17} $$
$$ \tan \theta=\frac{O}{A}=\frac{15}{8} $$
(d)

$$ \begin{aligned} \sin \theta & =\frac{O}{H} \\ & =\frac{10}{26} \\ & =\frac{5}{13} \end{aligned} $$
$$ \begin{aligned} \operatorname{kos} \theta & =\frac{A}{H} \\ & =\frac{24}{26} \\ & =\frac{12}{13} \end{aligned} $$
$$ \begin{aligned} \tan \theta & =\frac{O}{A} \\ & =\frac{10}{24} \\ & =\frac{5}{12} \end{aligned} $$
(e)
$$ \begin{aligned} \sin \theta & =\frac{O}{H} \\ & =\frac{3}{3.4} \\ & =\frac{15}{17} \end{aligned} $$
$$ \begin{aligned} \operatorname{kos} \theta & =\frac{A}{H} \\ & =\frac{1.6}{3.4} \\ & =\frac{8}{17} \end{aligned} $$
$$ \begin{aligned} \tan \theta & =\frac{O}{A} \\ & =\frac{3}{1.6} \\ & =\frac{15}{8} \end{aligned} $$
(f)

$$ \begin{aligned} \sin \theta & =\frac{O}{H} \\ & =\frac{0.6}{1} \\ & =\frac{6}{10} \\ & =\frac{3}{5} \end{aligned} $$
$$ \begin{aligned} \operatorname{kos} \theta & =\frac{A}{H} \\ & =\frac{0.8}{1} \\ & =\frac{8}{10} \\ & =\frac{4}{5} \end{aligned} $$
$$ \begin{aligned} \tan \theta & =\frac{O}{A} \\ & =\frac{0.6}{0.8} \\ & =\frac{3}{4} \end{aligned} $$
Soalan 2:
Hitung nilai x tanpa melukis sebarang segi tiga bersudut tegak atau menggunakan teorem Pythagoras atau dengan menggunakan kalkulator.
$$ \text { (a) } \sin \theta=\frac{1}{2}, \operatorname{kos} \theta=\frac{\sqrt{3}}{2}, \tan \theta=x $$
$$ \text { (b) } \sin \theta=\frac{1}{\sqrt{2}}, \operatorname{kos} \theta=x, \tan \theta=1 $$
$$ \text { (c) } \sin \theta=x, \operatorname{kos} \theta=\frac{5}{8}, \tan \theta=\frac{\sqrt{39}}{5} $$
$$ \text { (d) } \sin \theta=\frac{7}{9}, \operatorname{kos} \theta=x, \tan \theta=\frac{7}{4 \sqrt{2}} $$
Penyelesaian:
(a)
$$ \begin{aligned} \tan \theta & =\frac{\sin \theta}{\operatorname{kos} \theta} \\ x & =\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}} \\ x & =\frac{1}{2} \times \frac{2}{\sqrt{3}} \\ & =\frac{1}{\sqrt{3}} \end{aligned} $$
(b)
$$ \begin{aligned} \tan \theta & =\frac{\sin \theta}{\operatorname{kos} \theta} \\ 1 & =\frac{\frac{1}{\sqrt{2}}}{x} \\ x & =\frac{1}{\sqrt{2}} \end{aligned} $$
(c)
$$ \begin{aligned} \tan \theta & =\frac{\sin \theta}{\operatorname{kos} \theta} \\ \frac{\sqrt{39}}{5} & =\frac{x}{\frac{5}{8}} \\ \frac{\sqrt{39}}{5} \times \frac{5}{8} & =x \\ x & =\frac{\sqrt{39}}{8} \end{aligned} $$
(d)
$$ \begin{aligned} \tan \theta & =\frac{\sin \theta}{\operatorname{kos} \theta} \\ \frac{7}{4 \sqrt{2}} & =\frac{\frac{7}{9}}{x} \\ x & =\frac{7}{9} \times \frac{4 \sqrt{2}}{7} \\ & =\frac{4 \sqrt{2}}{9} \end{aligned} $$
Hitung nilai x tanpa melukis sebarang segi tiga bersudut tegak atau menggunakan teorem Pythagoras atau dengan menggunakan kalkulator.
$$ \text { (a) } \sin \theta=\frac{1}{2}, \operatorname{kos} \theta=\frac{\sqrt{3}}{2}, \tan \theta=x $$
$$ \text { (b) } \sin \theta=\frac{1}{\sqrt{2}}, \operatorname{kos} \theta=x, \tan \theta=1 $$
$$ \text { (c) } \sin \theta=x, \operatorname{kos} \theta=\frac{5}{8}, \tan \theta=\frac{\sqrt{39}}{5} $$
$$ \text { (d) } \sin \theta=\frac{7}{9}, \operatorname{kos} \theta=x, \tan \theta=\frac{7}{4 \sqrt{2}} $$
Penyelesaian:
(a)
$$ \begin{aligned} \tan \theta & =\frac{\sin \theta}{\operatorname{kos} \theta} \\ x & =\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}} \\ x & =\frac{1}{2} \times \frac{2}{\sqrt{3}} \\ & =\frac{1}{\sqrt{3}} \end{aligned} $$
(b)
$$ \begin{aligned} \tan \theta & =\frac{\sin \theta}{\operatorname{kos} \theta} \\ 1 & =\frac{\frac{1}{\sqrt{2}}}{x} \\ x & =\frac{1}{\sqrt{2}} \end{aligned} $$
(c)
$$ \begin{aligned} \tan \theta & =\frac{\sin \theta}{\operatorname{kos} \theta} \\ \frac{\sqrt{39}}{5} & =\frac{x}{\frac{5}{8}} \\ \frac{\sqrt{39}}{5} \times \frac{5}{8} & =x \\ x & =\frac{\sqrt{39}}{8} \end{aligned} $$
(d)
$$ \begin{aligned} \tan \theta & =\frac{\sin \theta}{\operatorname{kos} \theta} \\ \frac{7}{4 \sqrt{2}} & =\frac{\frac{7}{9}}{x} \\ x & =\frac{7}{9} \times \frac{4 \sqrt{2}}{7} \\ & =\frac{4 \sqrt{2}}{9} \end{aligned} $$