Soalan 1:
Rajah di bawah menunjukkan segi tiga P yang merupakan lukisan berskala bagi segi tiga Q dengan skala 1 : n. Hitung nilai n.
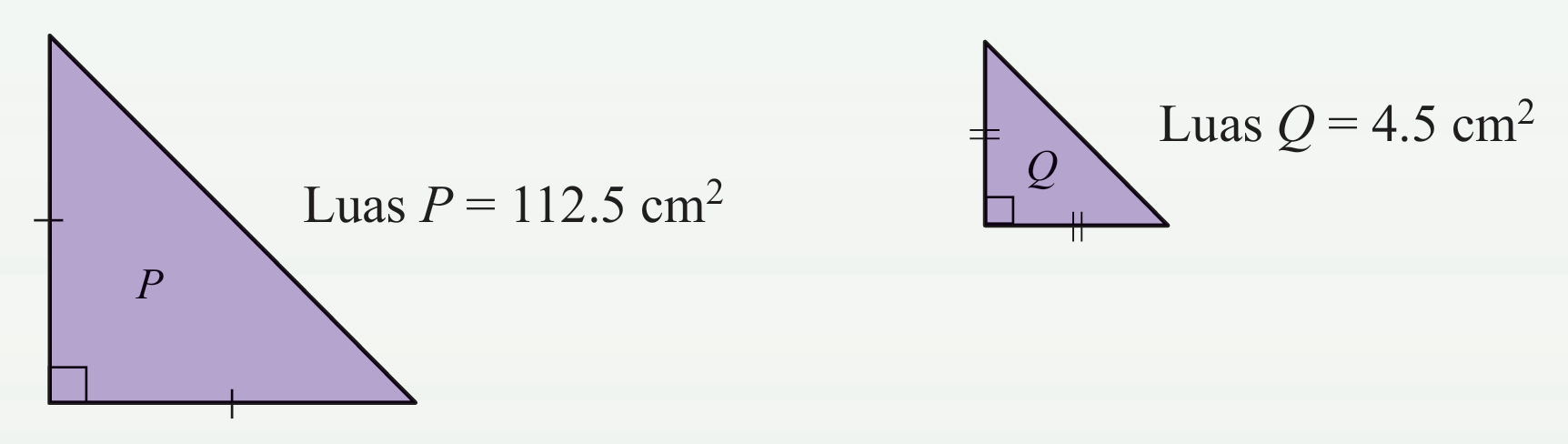
Penyelesaian:
$$ \begin{aligned} \text { Katakan } x & =\text { tinggi dan tapak segi tiga } \mathrm{P} \\ y & =\text { tinggi dan tapak segi tiga } \mathrm{Q} \end{aligned} $$
$$ \begin{aligned} &\text { Luas segi tiga } P=\frac{1}{2} \times \text { tapak } \times \text { tinggi }\\ &\begin{aligned} 112.5 & =\frac{1}{2} \times x \times x \\ 225 & =x^2 \\ x & =15 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Luas segi tiga } Q=\frac{1}{2} \times \text { tapak } \times \text { tinggi }\\ &\begin{aligned} 4.5 & =\frac{1}{2} \times y \times y \\ 9 & =y^2 \\ y & =3 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Skala } & =\frac{\text { Sisi lukisan berskala }}{\text { Sisi objek yang sepadan }} \\ \frac{1}{n} & =\frac{15 \mathrm{~cm}}{3 \mathrm{~cm}} \\ \frac{1}{n} & =5 \\ n & =\frac{1}{5} \end{aligned} $$
Rajah di bawah menunjukkan segi tiga P yang merupakan lukisan berskala bagi segi tiga Q dengan skala 1 : n. Hitung nilai n.

Penyelesaian:
$$ \begin{aligned} \text { Katakan } x & =\text { tinggi dan tapak segi tiga } \mathrm{P} \\ y & =\text { tinggi dan tapak segi tiga } \mathrm{Q} \end{aligned} $$
$$ \begin{aligned} &\text { Luas segi tiga } P=\frac{1}{2} \times \text { tapak } \times \text { tinggi }\\ &\begin{aligned} 112.5 & =\frac{1}{2} \times x \times x \\ 225 & =x^2 \\ x & =15 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Luas segi tiga } Q=\frac{1}{2} \times \text { tapak } \times \text { tinggi }\\ &\begin{aligned} 4.5 & =\frac{1}{2} \times y \times y \\ 9 & =y^2 \\ y & =3 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Skala } & =\frac{\text { Sisi lukisan berskala }}{\text { Sisi objek yang sepadan }} \\ \frac{1}{n} & =\frac{15 \mathrm{~cm}}{3 \mathrm{~cm}} \\ \frac{1}{n} & =5 \\ n & =\frac{1}{5} \end{aligned} $$
Soalan 2:
Rajah di bawah menunjukkan lima segi empat tepat.
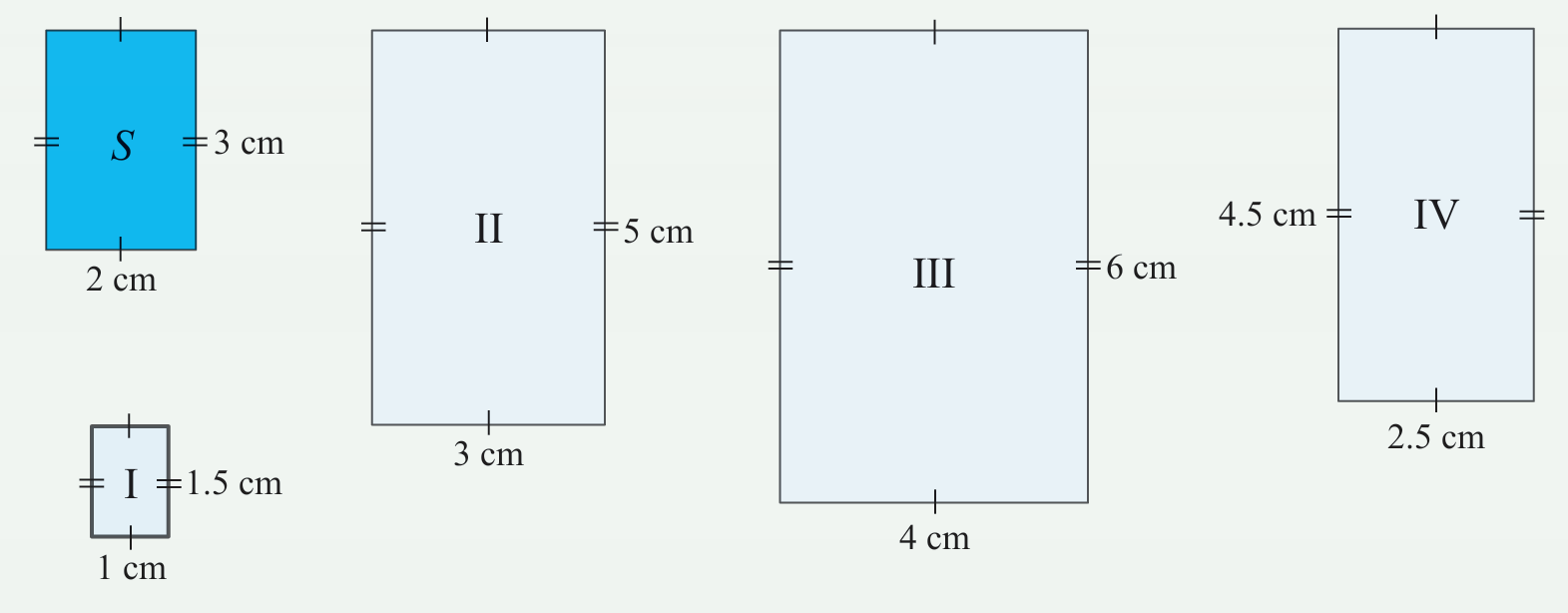
(a) Antara segi empat tepat I, II, III, dan IV, yang manakah merupakan lukisan berskala bagi segi empat tepat S di bawah skala tertentu?
(b) Bagi setiap jawapan anda di (a), tentukan skala yang digunakan.
(c)
i. Hitung luas setiap segi empat tepat, dalam cm2, bagi jawapan anda di (a).
ii. Tentukan nisbah luas S kepada luas setiap jawapan anda di (c) i.
Apakah kesimpulan anda berkaitan nisbah yang diperoleh?
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Bagi segi empat tepat I, }\\ &\frac{1 \mathrm{~cm}}{2 \mathrm{~cm}}=\frac{1.5 \mathrm{~cm}}{3 \mathrm{~cm}}=\frac{1}{2} \end{aligned} $$
Maka, segi empat tepat I adalah lukisan berskala bagi segi empat tepat S.
$$ \begin{aligned} &\text { Bagi segi empat tepat II, }\\ &\frac{3 \mathrm{~cm}}{2 \mathrm{~cm}} \neq \frac{5 \mathrm{~cm}}{3 \mathrm{~cm}} \end{aligned} $$
Maka, segi empat tepat II bukan lukisan berskala bagi segi empat tepat S.
$$ \begin{aligned} &\text { Bagi segi empat tepat III, }\\ &\frac{4 \mathrm{~cm}}{2 \mathrm{~cm}}=\frac{6 \mathrm{~cm}}{3 \mathrm{~cm}}=\frac{2}{1} \end{aligned} $$
Maka, segi empat tepat III adalah lukisan berskala bagi segi empat tepat S.
$$ \begin{aligned} &\text { Bagi segi empat tepat IV, }\\ &\frac{2.5 \mathrm{~cm}}{2 \mathrm{~cm}} \neq \frac{4.5 \mathrm{~cm}}{3 \mathrm{~cm}} \end{aligned} $$
Maka, segi empat tepat IV bukan lukisan berskala bagi segi empat tepat S.
(b)
$$ \begin{aligned} &\text { Bagi segi empat tepat I, }\\ &\begin{aligned} \frac{1 \mathrm{~cm}}{2 \mathrm{~cm}} & =\frac{1.5 \mathrm{~cm}}{3 \mathrm{~cm}}=\frac{1}{2} \\ \text { Skala } & =\frac{1}{2}: 1 \\ & =\frac{\frac{1}{2}}{\frac{1}{2}}: \frac{1}{\frac{1}{2}} \\ & =1: 2 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Bagi segi empat tepat III, }\\ &\begin{aligned} \frac{4 \mathrm{~cm}}{2 \mathrm{~cm}} & =\frac{6 \mathrm{~cm}}{3 \mathrm{~cm}}=\frac{2}{1} \\ \text { Skala } & =2: 1 \\ & =\frac{2}{2}: \frac{1}{2} \\ & =1: \frac{1}{2} \end{aligned} \end{aligned} $$
(c)(i)
$$ \begin{aligned} &\text { Luas segi empat tepat S, }\\ &\begin{aligned} & =2 \mathrm{~cm} \times 3 \mathrm{~cm} \\ & =6 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Luas segi empat tepat I, }\\ &\begin{aligned} & =1 \mathrm{~cm} \times 1.5 \mathrm{~cm} \\ & =1.5 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Luas segi empat tepat III, }\\ &\begin{aligned} & =4 \mathrm{~cm} \times 6 \mathrm{~cm} \\ & =24 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
(c)(ii)
$$ \begin{aligned} &\text { Nisbah luas } S \text { kepada luas } I \text { (dalam } 1 \text { : } n \text { ) }\\ &\begin{aligned} & =1.5: 6 \\ & =\frac{1.5}{1.5}: \frac{6}{1.5} \\ & =1: 4 \quad(\text { Skala lukisan berskala }=1: 2) \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Nisbah luas } S \text { kepada luas III }\\ &\begin{aligned} & =24: 6 \\ & =\frac{24}{24}: \frac{6}{24} \\ & =1: \frac{1}{4} \quad\left(\text { Skala lukisan berskala }=1: \frac{1}{2}\right) \end{aligned} \end{aligned} $$
Maka, Nisbah luas tidak berkadaran dengan skala lukisan berskala.
Rajah di bawah menunjukkan lima segi empat tepat.

(a) Antara segi empat tepat I, II, III, dan IV, yang manakah merupakan lukisan berskala bagi segi empat tepat S di bawah skala tertentu?
(b) Bagi setiap jawapan anda di (a), tentukan skala yang digunakan.
(c)
i. Hitung luas setiap segi empat tepat, dalam cm2, bagi jawapan anda di (a).
ii. Tentukan nisbah luas S kepada luas setiap jawapan anda di (c) i.
Apakah kesimpulan anda berkaitan nisbah yang diperoleh?
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Bagi segi empat tepat I, }\\ &\frac{1 \mathrm{~cm}}{2 \mathrm{~cm}}=\frac{1.5 \mathrm{~cm}}{3 \mathrm{~cm}}=\frac{1}{2} \end{aligned} $$
Maka, segi empat tepat I adalah lukisan berskala bagi segi empat tepat S.
$$ \begin{aligned} &\text { Bagi segi empat tepat II, }\\ &\frac{3 \mathrm{~cm}}{2 \mathrm{~cm}} \neq \frac{5 \mathrm{~cm}}{3 \mathrm{~cm}} \end{aligned} $$
Maka, segi empat tepat II bukan lukisan berskala bagi segi empat tepat S.
$$ \begin{aligned} &\text { Bagi segi empat tepat III, }\\ &\frac{4 \mathrm{~cm}}{2 \mathrm{~cm}}=\frac{6 \mathrm{~cm}}{3 \mathrm{~cm}}=\frac{2}{1} \end{aligned} $$
Maka, segi empat tepat III adalah lukisan berskala bagi segi empat tepat S.
$$ \begin{aligned} &\text { Bagi segi empat tepat IV, }\\ &\frac{2.5 \mathrm{~cm}}{2 \mathrm{~cm}} \neq \frac{4.5 \mathrm{~cm}}{3 \mathrm{~cm}} \end{aligned} $$
Maka, segi empat tepat IV bukan lukisan berskala bagi segi empat tepat S.
(b)
$$ \begin{aligned} &\text { Bagi segi empat tepat I, }\\ &\begin{aligned} \frac{1 \mathrm{~cm}}{2 \mathrm{~cm}} & =\frac{1.5 \mathrm{~cm}}{3 \mathrm{~cm}}=\frac{1}{2} \\ \text { Skala } & =\frac{1}{2}: 1 \\ & =\frac{\frac{1}{2}}{\frac{1}{2}}: \frac{1}{\frac{1}{2}} \\ & =1: 2 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Bagi segi empat tepat III, }\\ &\begin{aligned} \frac{4 \mathrm{~cm}}{2 \mathrm{~cm}} & =\frac{6 \mathrm{~cm}}{3 \mathrm{~cm}}=\frac{2}{1} \\ \text { Skala } & =2: 1 \\ & =\frac{2}{2}: \frac{1}{2} \\ & =1: \frac{1}{2} \end{aligned} \end{aligned} $$
(c)(i)
$$ \begin{aligned} &\text { Luas segi empat tepat S, }\\ &\begin{aligned} & =2 \mathrm{~cm} \times 3 \mathrm{~cm} \\ & =6 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Luas segi empat tepat I, }\\ &\begin{aligned} & =1 \mathrm{~cm} \times 1.5 \mathrm{~cm} \\ & =1.5 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Luas segi empat tepat III, }\\ &\begin{aligned} & =4 \mathrm{~cm} \times 6 \mathrm{~cm} \\ & =24 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
(c)(ii)
$$ \begin{aligned} &\text { Nisbah luas } S \text { kepada luas } I \text { (dalam } 1 \text { : } n \text { ) }\\ &\begin{aligned} & =1.5: 6 \\ & =\frac{1.5}{1.5}: \frac{6}{1.5} \\ & =1: 4 \quad(\text { Skala lukisan berskala }=1: 2) \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Nisbah luas } S \text { kepada luas III }\\ &\begin{aligned} & =24: 6 \\ & =\frac{24}{24}: \frac{6}{24} \\ & =1: \frac{1}{4} \quad\left(\text { Skala lukisan berskala }=1: \frac{1}{2}\right) \end{aligned} \end{aligned} $$
Maka, Nisbah luas tidak berkadaran dengan skala lukisan berskala.
Soalan 3:
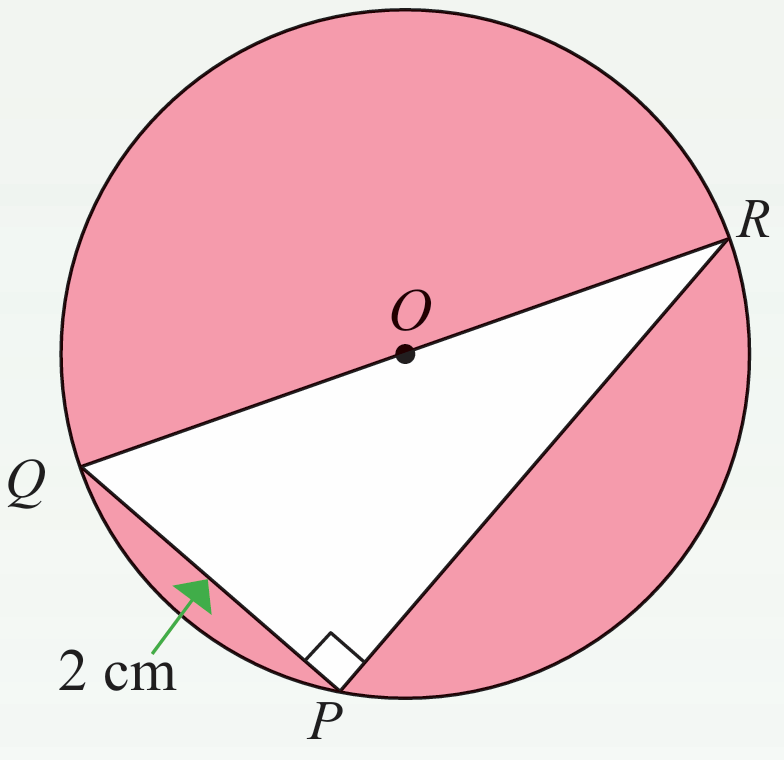
Rajah di sebelah menunjukkan suatu lukisan berskala bagi bulatan berpusat di O dan segi tiga PQR. Diberi bahawa diameter bulatan ialah 6 cm dan skala lukisan ialah 1 : 3.
(a) Hitung panjang sebenar PR dalam cm. Nyatakan jawapan anda betul kepada 3 angka bererti.
(b) Dengan menggunakan jawapan anda di (a), hitung luas kawasan berlorek yang sebenar dalam cm2. Nyatakan jawapan betul kepada 4 angka bererti.
Penyelesaian:
(a)
$$ \begin{aligned} \text { Skala } & =\frac{\text { Panjang pada lukisan berskala }}{\text { Panjang sebenar }} \\ \frac{1}{3} & =\frac{R Q \text { pada lukisan berskala }}{\text { Panjang sebenar } R Q} \\ \frac{1}{3} & =\frac{6 \mathrm{~cm}}{\text { Panjang sebenar } R Q} \\ \text { Panjang sebenar } R Q & =6 \mathrm{~cm} \times 3 \\ & =18 \mathrm{~cm} \end{aligned} $$
$$ \text { Panjang sebenar } \begin{aligned} P Q & =2 \mathrm{~cm} \times 3 \\ & =6 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} &\text { Guna teorem Pythagoras, }\\ &\begin{aligned} \text { Panjang sebenar } P R & =\sqrt{18^2-6^2} \\ & =\sqrt{288} \\ & =17.0 \mathrm{~cm}(3 . \mathrm{a} . \mathrm{b}) \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Kawasan berlorek yang sebenar }\\ &\begin{aligned} & =\pi j^2-\frac{1}{2} \times P Q \times P R \\ & =\left(\frac{22}{7} \times 9^2\right)-\left(\frac{1}{2} \times 6 \times 17\right) \\ & =254.571-51 \\ & =203.6 \mathrm{~cm}^2(4 . a \cdot b) \end{aligned} \end{aligned} $$

Rajah di sebelah menunjukkan suatu lukisan berskala bagi bulatan berpusat di O dan segi tiga PQR. Diberi bahawa diameter bulatan ialah 6 cm dan skala lukisan ialah 1 : 3.
(a) Hitung panjang sebenar PR dalam cm. Nyatakan jawapan anda betul kepada 3 angka bererti.
(b) Dengan menggunakan jawapan anda di (a), hitung luas kawasan berlorek yang sebenar dalam cm2. Nyatakan jawapan betul kepada 4 angka bererti.
Penyelesaian:
(a)
$$ \begin{aligned} \text { Skala } & =\frac{\text { Panjang pada lukisan berskala }}{\text { Panjang sebenar }} \\ \frac{1}{3} & =\frac{R Q \text { pada lukisan berskala }}{\text { Panjang sebenar } R Q} \\ \frac{1}{3} & =\frac{6 \mathrm{~cm}}{\text { Panjang sebenar } R Q} \\ \text { Panjang sebenar } R Q & =6 \mathrm{~cm} \times 3 \\ & =18 \mathrm{~cm} \end{aligned} $$
$$ \text { Panjang sebenar } \begin{aligned} P Q & =2 \mathrm{~cm} \times 3 \\ & =6 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} &\text { Guna teorem Pythagoras, }\\ &\begin{aligned} \text { Panjang sebenar } P R & =\sqrt{18^2-6^2} \\ & =\sqrt{288} \\ & =17.0 \mathrm{~cm}(3 . \mathrm{a} . \mathrm{b}) \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Kawasan berlorek yang sebenar }\\ &\begin{aligned} & =\pi j^2-\frac{1}{2} \times P Q \times P R \\ & =\left(\frac{22}{7} \times 9^2\right)-\left(\frac{1}{2} \times 6 \times 17\right) \\ & =254.571-51 \\ & =203.6 \mathrm{~cm}^2(4 . a \cdot b) \end{aligned} \end{aligned} $$