Soalan 1:
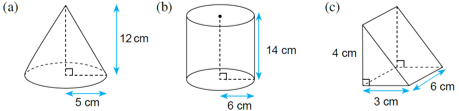
Hitung luas permukaan objek bentuk geometri tiga dimensi berikut.
Penyelesaian:
(a)
$$ \begin{aligned} \text { Luas permukaan kon } & =\pi j^2+\pi j s \\ & =\left(\frac{22}{7} \times 5^2\right)+\left[\frac{22}{7} \times 5 \times\left(\sqrt{12^2+5^2}\right)\right] \\ & =\left(\frac{22}{7} \times 25\right)+\left(\frac{22}{7} \times 5 \times 13\right) \\ & =78 \frac{4}{7}+204 \frac{2}{7} \\ & =282 \frac{6}{7} \\ & =282.86 \mathrm{~cm}^2 \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Luas permukaan silinder }=2 \pi j^2+2 \pi j t\\ &\begin{aligned} & =\left(2 \times \frac{22}{7} \times 6^2\right)+\left(2 \times \frac{22}{7} \times 6 \times 14\right) \\ & =226 \frac{2}{7}+528 \\ & =754 \frac{2}{7} \\ & =754.29 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Luas permukaan prisma }\\ &\begin{aligned} & =(2 \times \text { luas segi tiga })+(3 \times \text { luas tapak segi empat }) \\ & =2\left(\frac{1}{2} \times 3 \times 4\right)+(4 \times 6)+(3 \times 6)+\left(6 \times \sqrt{4^2+3^2}\right) \\ & =12+24+18+30 \\ & =84 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
Hitung luas permukaan objek bentuk geometri tiga dimensi berikut.

Penyelesaian:
(a)
$$ \begin{aligned} \text { Luas permukaan kon } & =\pi j^2+\pi j s \\ & =\left(\frac{22}{7} \times 5^2\right)+\left[\frac{22}{7} \times 5 \times\left(\sqrt{12^2+5^2}\right)\right] \\ & =\left(\frac{22}{7} \times 25\right)+\left(\frac{22}{7} \times 5 \times 13\right) \\ & =78 \frac{4}{7}+204 \frac{2}{7} \\ & =282 \frac{6}{7} \\ & =282.86 \mathrm{~cm}^2 \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Luas permukaan silinder }=2 \pi j^2+2 \pi j t\\ &\begin{aligned} & =\left(2 \times \frac{22}{7} \times 6^2\right)+\left(2 \times \frac{22}{7} \times 6 \times 14\right) \\ & =226 \frac{2}{7}+528 \\ & =754 \frac{2}{7} \\ & =754.29 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Luas permukaan prisma }\\ &\begin{aligned} & =(2 \times \text { luas segi tiga })+(3 \times \text { luas tapak segi empat }) \\ & =2\left(\frac{1}{2} \times 3 \times 4\right)+(4 \times 6)+(3 \times 6)+\left(6 \times \sqrt{4^2+3^2}\right) \\ & =12+24+18+30 \\ & =84 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
Soalan 2:
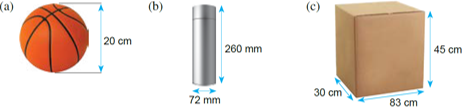
Hitung luas permukaan objek berikut.
Penyelesaian:
(a)
$$ \begin{aligned} \text { Luas permukaan sfera } & =4 \pi j^2 \\ & =4 \times \frac{22}{7} \times 10^2 \\ & =1257 \frac{1}{7} \\ & =1257.14 \mathrm{~cm}^2 \end{aligned} $$
(b)
$$ \begin{aligned} \text { Luas permukaan silinder } & =2 \pi j^2+2 \pi j t \\ & =\left(2 \times \frac{22}{7} \times 36^2\right)+\left(2 \times \frac{22}{7} \times 36 \times 260\right) \\ & =8146 \frac{2}{7}+58834 \frac{2}{7} \\ & =66980 \frac{4}{7} \\ & =66980.57 \mathrm{~mm}^2 \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Luas permukaan kuboid }\\ &\begin{aligned} = & (2 \times \text { luas segi empat tepat })+(2 \times \text { luas segi empat tepat }) \\ & +(2 \times \text { luas segi empat tepat }) \\ = & (2 \times 83 \times 45)+(2 \times 30 \times 45)+(2 \times 30 \times 83) \\ = & 7470+2700+4980 \\ = & 15150 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
Hitung luas permukaan objek berikut.

Penyelesaian:
(a)
$$ \begin{aligned} \text { Luas permukaan sfera } & =4 \pi j^2 \\ & =4 \times \frac{22}{7} \times 10^2 \\ & =1257 \frac{1}{7} \\ & =1257.14 \mathrm{~cm}^2 \end{aligned} $$
(b)
$$ \begin{aligned} \text { Luas permukaan silinder } & =2 \pi j^2+2 \pi j t \\ & =\left(2 \times \frac{22}{7} \times 36^2\right)+\left(2 \times \frac{22}{7} \times 36 \times 260\right) \\ & =8146 \frac{2}{7}+58834 \frac{2}{7} \\ & =66980 \frac{4}{7} \\ & =66980.57 \mathrm{~mm}^2 \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Luas permukaan kuboid }\\ &\begin{aligned} = & (2 \times \text { luas segi empat tepat })+(2 \times \text { luas segi empat tepat }) \\ & +(2 \times \text { luas segi empat tepat }) \\ = & (2 \times 83 \times 45)+(2 \times 30 \times 45)+(2 \times 30 \times 83) \\ = & 7470+2700+4980 \\ = & 15150 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
Soalan 3:
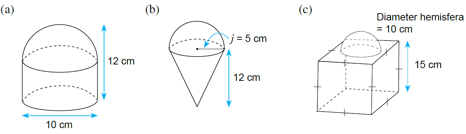
Hitung luas permukaan gabungan bentuk geometri tiga dimensi berikut.
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Luas permukaan gabungan }\\ &\begin{aligned} = & \text { Luas permukaan bulatan }+ \text { Luas segi empat } \\ & + \text { Luas permukaan hemisfera } \\ = & \pi j^2+2 \pi j t+\left(\frac{1}{2} \times 4 \pi j^2\right) \\ = & \left(\frac{22}{7} \times 5^2\right)+\left[2 \times \frac{22}{7} \times 5 \times(12-5)\right]+\left(\frac{1}{2} \times 4 \times \frac{22}{7} \times 5^2\right) \\ = & 78 \frac{4}{7}+220+157 \frac{1}{7} \\ = & 455.71 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Luas permukaan gabungan }\\ &\begin{aligned} & =\text { Luas permukaan melengkung }+ \text { Luas permukaan hemisfera } \\ & =\pi j s+2 \pi j^2 \\ & =\left[\frac{22}{7} \times 5 \times\left(\sqrt{12^2+5^2}\right)\right]+\left(2 \times \frac{22}{7} \times 5^2\right) \\ & =\left(\frac{22}{7} \times 5 \times 13\right)+\left(2 \times \frac{22}{7} \times 25\right) \\ & =204 \frac{2}{7}+157 \frac{1}{7} \\ & =361 \frac{3}{7} \\ & =361.43 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Luas permukaan gabungan }\\ &\begin{aligned} & =6 \times \text { luas segi empat sama }- \text { luas bulatan }+ \text { Luas permukaan hemisfera } \\ & =(6 \times 15 \times 15)-\left(\frac{22}{7} \times 5^2\right)+\left(2 \times \frac{22}{7} \times 5^2\right) \\ & =1350-78 \frac{4}{7}+157 \frac{1}{7} \\ & =1428 \frac{4}{7} \\ & =1428.57 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
Hitung luas permukaan gabungan bentuk geometri tiga dimensi berikut.

Penyelesaian:
(a)
$$ \begin{aligned} &\text { Luas permukaan gabungan }\\ &\begin{aligned} = & \text { Luas permukaan bulatan }+ \text { Luas segi empat } \\ & + \text { Luas permukaan hemisfera } \\ = & \pi j^2+2 \pi j t+\left(\frac{1}{2} \times 4 \pi j^2\right) \\ = & \left(\frac{22}{7} \times 5^2\right)+\left[2 \times \frac{22}{7} \times 5 \times(12-5)\right]+\left(\frac{1}{2} \times 4 \times \frac{22}{7} \times 5^2\right) \\ = & 78 \frac{4}{7}+220+157 \frac{1}{7} \\ = & 455.71 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Luas permukaan gabungan }\\ &\begin{aligned} & =\text { Luas permukaan melengkung }+ \text { Luas permukaan hemisfera } \\ & =\pi j s+2 \pi j^2 \\ & =\left[\frac{22}{7} \times 5 \times\left(\sqrt{12^2+5^2}\right)\right]+\left(2 \times \frac{22}{7} \times 5^2\right) \\ & =\left(\frac{22}{7} \times 5 \times 13\right)+\left(2 \times \frac{22}{7} \times 25\right) \\ & =204 \frac{2}{7}+157 \frac{1}{7} \\ & =361 \frac{3}{7} \\ & =361.43 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Luas permukaan gabungan }\\ &\begin{aligned} & =6 \times \text { luas segi empat sama }- \text { luas bulatan }+ \text { Luas permukaan hemisfera } \\ & =(6 \times 15 \times 15)-\left(\frac{22}{7} \times 5^2\right)+\left(2 \times \frac{22}{7} \times 5^2\right) \\ & =1350-78 \frac{4}{7}+157 \frac{1}{7} \\ & =1428 \frac{4}{7} \\ & =1428.57 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$