Soalan 7:
Suatu nombor ditambah kepada 7, hasilnya ialah x. Jika nombor itu dibahagi dengan 2, hasilnya ialah y. Terangkan bagaimana anda menentukan nilai bagi x + y jika nilai nombor itu diketahui.
Penyelesaian:
$$ \begin{aligned} &\text { Katakan } n \text { mewakili suatu nombor }\\ &\begin{aligned} n+7 & =x \\ n \div 2 & =y \\ x+y & =(n+7)+(n \div 2) \\ & =n+7+\frac{n}{2} \\ & =\frac{3 n}{2}+7 \end{aligned} \end{aligned} $$
Suatu nombor ditambah kepada 7, hasilnya ialah x. Jika nombor itu dibahagi dengan 2, hasilnya ialah y. Terangkan bagaimana anda menentukan nilai bagi x + y jika nilai nombor itu diketahui.
Penyelesaian:
$$ \begin{aligned} &\text { Katakan } n \text { mewakili suatu nombor }\\ &\begin{aligned} n+7 & =x \\ n \div 2 & =y \\ x+y & =(n+7)+(n \div 2) \\ & =n+7+\frac{n}{2} \\ & =\frac{3 n}{2}+7 \end{aligned} \end{aligned} $$
Soalan 8:
Sebuah kedai alat elektrik membeli 120 biji lampu filamen dengan kos RMp sebiji dan 180 biji lampu LED dengan kos RMq sebiji. Kedai itu kemudian menjual lampu secara promosi dengan 2 biji lampu filamen dan 3 biji lampu LED dengan harga RM(3h + 4k). Jika kedai itu dapat menjual semua lampu, ungkapkan keuntungan yang diperoleh dalam sebutan p, q, h dan k.
Penyelesaian:
$$ \begin{aligned} \text { Jumlah kos } & =\text { kos bagi lampu filamen }+ \text { kos bagi lampu LED } \\ & =(120)(p)+(180)(q) \\ & =\mathrm{RM}(120 p+180 q) \end{aligned} $$
Set bagi 2 biji lampu filamen = 120 ÷ 2 = 60 set
Set bagi 3 biji lampu LED = 180 ÷ 3 = 60 set
Harga promosi bagi lampu set = RM (3h + 4k)
$$ \begin{aligned} &\text { Hasil yang diperoleh dalam jualan lampu }\\ &\begin{aligned} & =60 \times \mathrm{RM}(3 h+4 k) \\ & =\mathrm{RM}(180 h+240 k) \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Keuntungan } & =\text { Hasil }- \text { Kos } \\ & =\mathrm{RM}(180 h+240 k)-\mathrm{RM}(120 p+180 q) \\ & =\mathrm{RM}(180 h+240 k-120 p-180 q) \\ & =\mathrm{RM} 60(3 h+4 k-2 p-3 q) \end{aligned} $$
Sebuah kedai alat elektrik membeli 120 biji lampu filamen dengan kos RMp sebiji dan 180 biji lampu LED dengan kos RMq sebiji. Kedai itu kemudian menjual lampu secara promosi dengan 2 biji lampu filamen dan 3 biji lampu LED dengan harga RM(3h + 4k). Jika kedai itu dapat menjual semua lampu, ungkapkan keuntungan yang diperoleh dalam sebutan p, q, h dan k.
Penyelesaian:
$$ \begin{aligned} \text { Jumlah kos } & =\text { kos bagi lampu filamen }+ \text { kos bagi lampu LED } \\ & =(120)(p)+(180)(q) \\ & =\mathrm{RM}(120 p+180 q) \end{aligned} $$
Set bagi 2 biji lampu filamen = 120 ÷ 2 = 60 set
Set bagi 3 biji lampu LED = 180 ÷ 3 = 60 set
Harga promosi bagi lampu set = RM (3h + 4k)
$$ \begin{aligned} &\text { Hasil yang diperoleh dalam jualan lampu }\\ &\begin{aligned} & =60 \times \mathrm{RM}(3 h+4 k) \\ & =\mathrm{RM}(180 h+240 k) \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Keuntungan } & =\text { Hasil }- \text { Kos } \\ & =\mathrm{RM}(180 h+240 k)-\mathrm{RM}(120 p+180 q) \\ & =\mathrm{RM}(180 h+240 k-120 p-180 q) \\ & =\mathrm{RM} 60(3 h+4 k-2 p-3 q) \end{aligned} $$
Soalan 9:
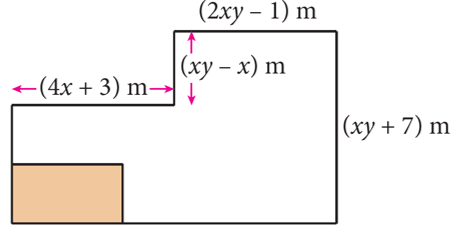
Rajah di sebelah menunjukkan sebuah kebun milik Norhaimi. Kawasan berlorek yang berbentuk segi empat tepat belum dibaja. Kawasan selebihnya ditanami sayur-sayuran. Norhaimi ingin memagari kawasan tanaman sayur-sayuran. Ungkapkan panjang dawai yang diperlukannya dalam sebutan x dan y.
Penyelesaian:
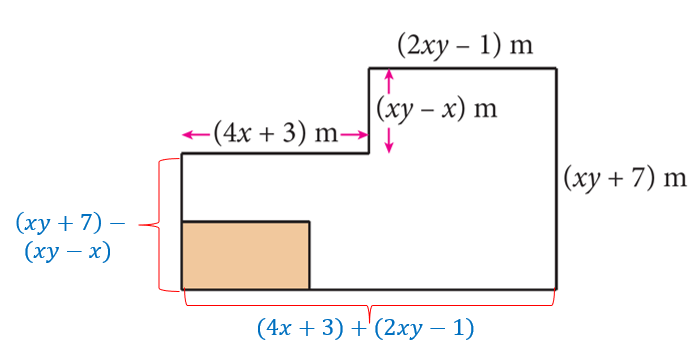
$$ \begin{aligned} &\text { Panjang dawai yang diperlukan untuk memagari kawsan tanaman }\\ &\begin{aligned} = & (4 x+3)+(x y-x)+(2 x y-1)+(x y+7) \\ & +(4 x+3)+(2 x y-1)+[(x y+7)-(x y-x)] \\ = & 4 x+3+x y-x+2 x y-1+x y+7+4 x+3 \\ & +2 x y-1+x y+7-x y+x \\ = & (8 x+6 x y+18) m \end{aligned} \end{aligned} $$

Rajah di sebelah menunjukkan sebuah kebun milik Norhaimi. Kawasan berlorek yang berbentuk segi empat tepat belum dibaja. Kawasan selebihnya ditanami sayur-sayuran. Norhaimi ingin memagari kawasan tanaman sayur-sayuran. Ungkapkan panjang dawai yang diperlukannya dalam sebutan x dan y.
Penyelesaian:

$$ \begin{aligned} &\text { Panjang dawai yang diperlukan untuk memagari kawsan tanaman }\\ &\begin{aligned} = & (4 x+3)+(x y-x)+(2 x y-1)+(x y+7) \\ & +(4 x+3)+(2 x y-1)+[(x y+7)-(x y-x)] \\ = & 4 x+3+x y-x+2 x y-1+x y+7+4 x+3 \\ & +2 x y-1+x y+7-x y+x \\ = & (8 x+6 x y+18) m \end{aligned} \end{aligned} $$
Soalan 10:
Suhu dalam unit darjah Celsius (°C) boleh ditukarkan kepada darjah Fahrenheit (°F) dengan menggunakan ungkapan 9/5 T + 32, dengan keadaan T ialah suhu dalam unit darjah Celsius. Apabila sejenis cecair dipanaskan daripada 18°C kepada 33°C, berapakah perubahan suhu cecair itu dalam unit darjah Fahrenheit?
Penyelesaian:
$$ \begin{aligned} &\text { Diberi pertukaran daripada darjah Celsius }\\ &\rightarrow \text { darjah Fahrenheit }=\frac{9}{5} T+32 \end{aligned} $$
$$ \begin{aligned} \text { Suhu awal dalam darjah Fahrenheit } & =\frac{9}{5}(18)+32 \\ & =\frac{162}{5}+32 \\ & =64.4^{\circ} \mathrm{F} \end{aligned} $$
$$ \begin{aligned} \text { Suhu akhir dalam darjah Fahrenheit } & =\frac{9}{5}(33)+32 \\ & =\frac{297}{5}+32 \\ & =91.4^{\circ} \mathrm{F} \end{aligned} $$
$$ \begin{aligned} \text { Perubahan suhu cecair } & =91.4^{\circ} \mathrm{F}-64.4 \mathrm{~F} \\ & =27^{\circ} \mathrm{F} \end{aligned} $$
Suhu dalam unit darjah Celsius (°C) boleh ditukarkan kepada darjah Fahrenheit (°F) dengan menggunakan ungkapan 9/5 T + 32, dengan keadaan T ialah suhu dalam unit darjah Celsius. Apabila sejenis cecair dipanaskan daripada 18°C kepada 33°C, berapakah perubahan suhu cecair itu dalam unit darjah Fahrenheit?
Penyelesaian:
$$ \begin{aligned} &\text { Diberi pertukaran daripada darjah Celsius }\\ &\rightarrow \text { darjah Fahrenheit }=\frac{9}{5} T+32 \end{aligned} $$
$$ \begin{aligned} \text { Suhu awal dalam darjah Fahrenheit } & =\frac{9}{5}(18)+32 \\ & =\frac{162}{5}+32 \\ & =64.4^{\circ} \mathrm{F} \end{aligned} $$
$$ \begin{aligned} \text { Suhu akhir dalam darjah Fahrenheit } & =\frac{9}{5}(33)+32 \\ & =\frac{297}{5}+32 \\ & =91.4^{\circ} \mathrm{F} \end{aligned} $$
$$ \begin{aligned} \text { Perubahan suhu cecair } & =91.4^{\circ} \mathrm{F}-64.4 \mathrm{~F} \\ & =27^{\circ} \mathrm{F} \end{aligned} $$