Soalan 1:
Tentukan sama ada titik berikut terletak pada garis lurus y = 2x + 16.
(a) M(– 4, 3)
(b) N(1, 18)
(c) P(–8, 0)
(d) Q(–5, 8)
Penyelesaian:
(a)
$$ \begin{aligned} y & =2 x+16, M(-4,3) \\ y & =2(-4)+16 \\ & =-8+16 \\ & =8 \end{aligned} $$
(b)
$$ \begin{aligned} y & =2 x+16, N(1,18) \\ y & =2(1)+16 \\ & =18 end{aligned} $$
(c)
$$ \begin{aligned} y & =2 x+16, P(-8,0) \\ y & =2(-8)+16 \\ & =-16+16 \\ & =0 \end{aligned} $$
Nilai sebelah kiri = nilai sebelah kanan
Maka, P(–8, 0) terletak pada garis lurus y = 2x + 16.
(d)
$$ \begin{aligned} y & =2 x+16, Q(-5,8) \\ y & =2(-5)+16 \\ & =6 \end{aligned} $$
Nilai sebelah kiri ≠ nilai sebelah kanan
Maka, Q(–5, 8) tidak terletak pada garis lurus y = 2x + 16.
Tentukan sama ada titik berikut terletak pada garis lurus y = 2x + 16.
(a) M(– 4, 3)
(b) N(1, 18)
(c) P(–8, 0)
(d) Q(–5, 8)
Penyelesaian:
(a)
$$ \begin{aligned} y & =2 x+16, M(-4,3) \\ y & =2(-4)+16 \\ & =-8+16 \\ & =8 \end{aligned} $$
Nilai sebelah kiri ≠ nilai sebelah kanan
Maka, M(-4, 3) terletak pada garis lurus y = 2x + 16.
$$ \begin{aligned} y & =2 x+16, N(1,18) \\ y & =2(1)+16 \\ & =18 end{aligned} $$
Nilai sebelah kiri = nilai sebelah kanan
Maka, N(1, 18) tidak terletak pada garis lurus y = 2x + 16.
(c)
$$ \begin{aligned} y & =2 x+16, P(-8,0) \\ y & =2(-8)+16 \\ & =-16+16 \\ & =0 \end{aligned} $$
Nilai sebelah kiri = nilai sebelah kanan
Maka, P(–8, 0) terletak pada garis lurus y = 2x + 16.
(d)
$$ \begin{aligned} y & =2 x+16, Q(-5,8) \\ y & =2(-5)+16 \\ & =6 \end{aligned} $$
Nilai sebelah kiri ≠ nilai sebelah kanan
Maka, Q(–5, 8) tidak terletak pada garis lurus y = 2x + 16.
Soalan 2:
Tentukan sama ada titik berikut terletak pada garis lurus 2x + 3y = 12.
(a) M(0, 4)
(b) N(3, –2)
(c) P(15, –6)
(d) Q(–4, 8)
Penyelesaian:
(a)
$$ \begin{gathered} 2 x+3 y=12, M(0,4) \\ 2(0)+3(4)=12 \\ 12=12 \end{gathered} $$
(b)
$$ \begin{aligned} & 2 x+3 y=12, N(3,-2) \\ & 2(3)+3(-2)=12 \\ & 6-6=12 \\ & 0 \neq 12 \end{aligned} $$
(c)
$$ \begin{aligned} & 2 x+3 y=12, P(15,-6) \\ & 2(15)+3(-6)=12 \\ & 30-18=12 \\ & 12=12 \end{aligned} $$
Nilai sebelah kiri = nilai sebelah kanan
Maka, P(15, –6) terletak pada garis lurus 2x + 3y = 12.
(d)
$$ \begin{gathered} 2 x+3 y=12, Q(-4,8) \\ 2(-4)+3(8)=12 \\ -8+24=12 \\ 16 \neq 12 \end{gathered} $$
Nilai sebelah kiri ≠ nilai sebelah kanan
Maka, Q(–4, 8) tidak terletak pada garis lurus 2x + 3y = 12.
Tentukan sama ada titik berikut terletak pada garis lurus 2x + 3y = 12.
(a) M(0, 4)
(b) N(3, –2)
(c) P(15, –6)
(d) Q(–4, 8)
Penyelesaian:
(a)
$$ \begin{gathered} 2 x+3 y=12, M(0,4) \\ 2(0)+3(4)=12 \\ 12=12 \end{gathered} $$
Nilai sebelah kiri = nilai sebelah kanan
Maka, M(0, 4) terletak pada garis lurus 2x + 3y = 12.
$$ \begin{aligned} & 2 x+3 y=12, N(3,-2) \\ & 2(3)+3(-2)=12 \\ & 6-6=12 \\ & 0 \neq 12 \end{aligned} $$
Nilai sebelah kiri ≠ nilai sebelah kanan
Maka, N(3, –2) tidak terletak pada garis lurus 2x + 3y = 12.
(c)
$$ \begin{aligned} & 2 x+3 y=12, P(15,-6) \\ & 2(15)+3(-6)=12 \\ & 30-18=12 \\ & 12=12 \end{aligned} $$
Nilai sebelah kiri = nilai sebelah kanan
Maka, P(15, –6) terletak pada garis lurus 2x + 3y = 12.
(d)
$$ \begin{gathered} 2 x+3 y=12, Q(-4,8) \\ 2(-4)+3(8)=12 \\ -8+24=12 \\ 16 \neq 12 \end{gathered} $$
Nilai sebelah kiri ≠ nilai sebelah kanan
Maka, Q(–4, 8) tidak terletak pada garis lurus 2x + 3y = 12.
Soalan 3:
$$ \text { Tentukan sama ada titik berikut terletak pada garis lurus } \frac{x}{2}+\frac{y}{3}=1 \text {. } $$
(a) M(2, 0)
(b) N(–2, 12)
(c) P(4, –3)
(d) Q(0, 6)
Penyelesaian:
$$ \text { Tentukan sama ada titik berikut terletak pada garis lurus } \frac{x}{2}+\frac{y}{3}=1 \text {. } $$
(a) M(2, 0)
(b) N(–2, 12)
(c) P(4, –3)
(d) Q(0, 6)
Penyelesaian:
(a)
$$ \begin{aligned} \frac{x}{2}+\frac{y}{3} & =1, M(2,0) \\ \frac{2}{2}+\frac{0}{3} & =1 \\ 1 & =1 \end{aligned} $$
Nilai sebelah kiri = nilai sebelah kanan
$$ \text { Maka, } M(2,0) \text { terletak pada garis lurus. } \frac{x}{2}+\frac{y}{3}=1 $$
(b)
$$ \begin{aligned} & \frac{x}{2}+\frac{y}{3}=1, N(-2,12) \\ & \frac{-2}{2}+\frac{12}{3}=1 \\ & -1+4=1 \\ & 3 \neq 1 \end{aligned} $$
Nilai sebelah kiri ≠ nilai sebelah kanan
$$ \text { Maka, } N(-2,12) \text { tidak terletak pada garis lurus } \frac{x}{2}+\frac{y}{3}=1 $$
(c)
$$ \begin{gathered} \frac{x}{2}+\frac{y}{3}=1, P(4,-3) \\ \frac{4}{2}+\frac{(-3)}{3}=1 \\ 2-1=1 \\ 1=1 \end{gathered} $$
Nilai sebelah kiri = nilai sebelah kanan
$$ \text { Maka, } P(4,-3) \text { terletak pada garis lurus } \frac{x}{2}+\frac{y}{3}=1 $$
(d)
$$ \begin{aligned} \frac{x}{2}+\frac{y}{3} & =1, Q(0,6) \\ \frac{0}{2}+\frac{6}{3} & =1 \\ 2 & \neq 1 \end{aligned} $$
Nilai sebelah kiri ≠ nilai sebelah kanan
$$ \text { Maka, } Q(0,6) \text { tidak terletak pada garis lurus } \frac{x}{2}+\frac{y}{3}=1 $$
$$ \begin{aligned} \frac{x}{2}+\frac{y}{3} & =1, M(2,0) \\ \frac{2}{2}+\frac{0}{3} & =1 \\ 1 & =1 \end{aligned} $$
Nilai sebelah kiri = nilai sebelah kanan
$$ \text { Maka, } M(2,0) \text { terletak pada garis lurus. } \frac{x}{2}+\frac{y}{3}=1 $$
(b)
$$ \begin{aligned} & \frac{x}{2}+\frac{y}{3}=1, N(-2,12) \\ & \frac{-2}{2}+\frac{12}{3}=1 \\ & -1+4=1 \\ & 3 \neq 1 \end{aligned} $$
Nilai sebelah kiri ≠ nilai sebelah kanan
$$ \text { Maka, } N(-2,12) \text { tidak terletak pada garis lurus } \frac{x}{2}+\frac{y}{3}=1 $$
(c)
$$ \begin{gathered} \frac{x}{2}+\frac{y}{3}=1, P(4,-3) \\ \frac{4}{2}+\frac{(-3)}{3}=1 \\ 2-1=1 \\ 1=1 \end{gathered} $$
Nilai sebelah kiri = nilai sebelah kanan
$$ \text { Maka, } P(4,-3) \text { terletak pada garis lurus } \frac{x}{2}+\frac{y}{3}=1 $$
(d)
$$ \begin{aligned} \frac{x}{2}+\frac{y}{3} & =1, Q(0,6) \\ \frac{0}{2}+\frac{6}{3} & =1 \\ 2 & \neq 1 \end{aligned} $$
Nilai sebelah kiri ≠ nilai sebelah kanan
$$ \text { Maka, } Q(0,6) \text { tidak terletak pada garis lurus } \frac{x}{2}+\frac{y}{3}=1 $$
Soalan 4:
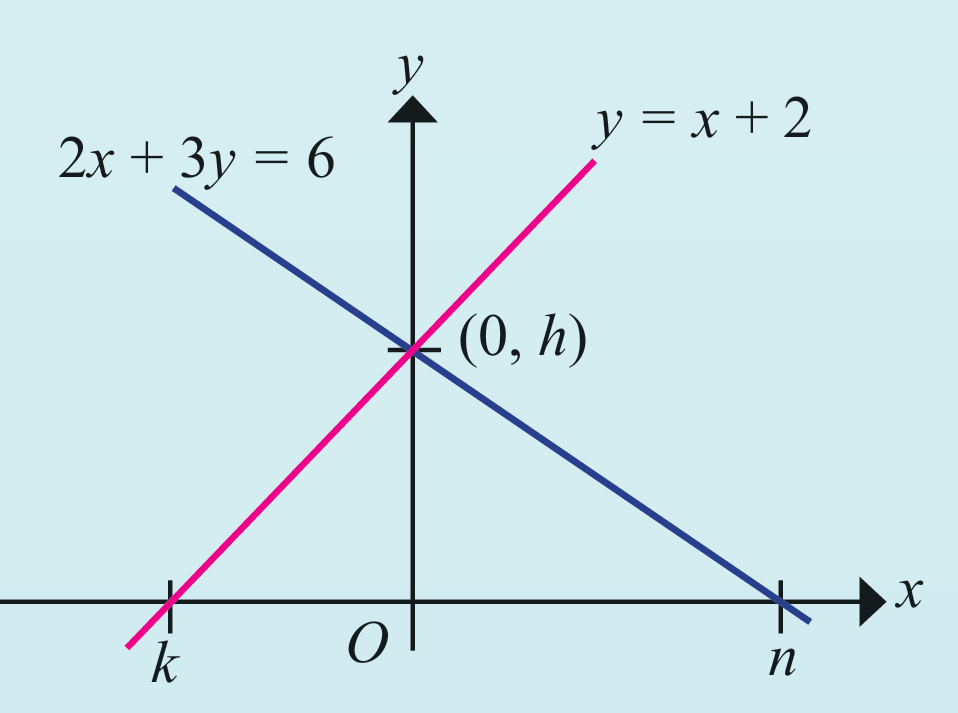
Rajah menunjukkan dua garis lurus, y = x + 2 dan 2x + 3y = 6. Diberi bahawa O adalah asalan. Tentukan nilai
(a) h
(b) k
(c) n
Penyelesaian:

Rajah menunjukkan dua garis lurus, y = x + 2 dan 2x + 3y = 6. Diberi bahawa O adalah asalan. Tentukan nilai
(a) h
(b) k
(c) n
Penyelesaian:
(a)
h merupakan pintasan-y. Maka, x = 0
$$ \begin{aligned} 2 x+3 y & =6 \\ 2(0)+3(h) & =6 \\ 3 h & =6 \\ h & =\frac{6}{3} \\ h & =2 \end{aligned} $$
(b)
k merupakan pintasan-x bagi y = x + 2. Maka, y = 0
$$ \begin{aligned} & y=x+2 \\ & 0=k+2 \\ & k=-2 \end{aligned} $$
(c)
n merupakan pintasan-x bagi 2x + 3y = 6. Maka, y = 0
$$ \begin{aligned} 2 n+3(0) & =6 \\ 2 n & =6 \\ n & =\frac{6}{2} \\ n & =3 \end{aligned} $$
h merupakan pintasan-y. Maka, x = 0
$$ \begin{aligned} 2 x+3 y & =6 \\ 2(0)+3(h) & =6 \\ 3 h & =6 \\ h & =\frac{6}{3} \\ h & =2 \end{aligned} $$
(b)
k merupakan pintasan-x bagi y = x + 2. Maka, y = 0
$$ \begin{aligned} & y=x+2 \\ & 0=k+2 \\ & k=-2 \end{aligned} $$
(c)
n merupakan pintasan-x bagi 2x + 3y = 6. Maka, y = 0
$$ \begin{aligned} 2 n+3(0) & =6 \\ 2 n & =6 \\ n & =\frac{6}{2} \\ n & =3 \end{aligned} $$