Tinggi asal pokok F ialah 9 cm. Tingginya ialah y cm selepas x hari dan dihubungkan oleh persamaan y = 3/16 x + 9. Pokok G mempunyai kadar pertumbuhan yang sama dengan pokok F. Pokok G mencapai tinggi 15 cm selepas 8 hari. Tentukan satu persamaan untuk mewakili tinggi pokok G. Seterusnya, nyatakan tinggi asal, dalam cm, pokok G.
Penyelesaian:
$$
\text { Kecerunan pokok } G=\text { Kecerunan pokok } F=\frac{3}{16}
$$
Gantikan nilai m, x = 8 dan y = 15 ke dalam y = mx + c
$$
\begin{aligned}
15 & =\frac{3}{16}(8)+c \\
15 & =\frac{24}{16}+c \\
c & =15-\frac{3}{2} \\
c & =\frac{27}{2}
\end{aligned}
$$
$$
\begin{aligned}
&\text { Maka persamaan yang mewakili tinggi pokok } G \text { ialah }\\
&y=\frac{3}{16} x+\frac{27}{2}
\end{aligned}
$$
$$
\begin{aligned}
&\text { Bila } x=0 \text {, tinggi asal pokok } G, y_0 \text { ialah }\\
&\begin{aligned}
y_0 & =\frac{3}{16}(0)+\frac{27}{2} \\
& =0+\frac{27}{2} \\
& =13.5 \mathrm{~cm}
\end{aligned}
\end{aligned}
$$
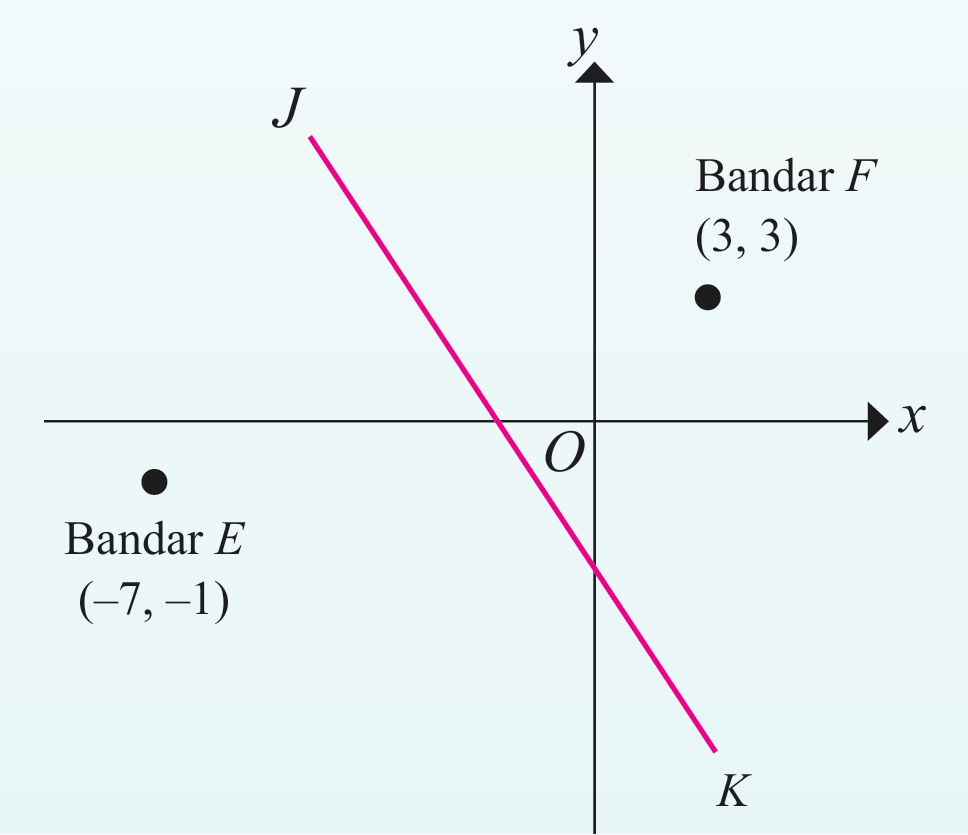
JK ialah sebatang jalan lurus yang melalui titik tengah di antara bandar E dengan bandar F.
(a) Persamaan bagi jalan lurus JK ialah y = –2x + k, dengan keadaan k ialah pemalar.
Tentukan nilai k.
(b) Satu jalan lurus yang lain, GH dengan persamaan y = 2x + 17 akan dibina. Satu lampu isyarat akan dipasang di persimpangan kedua-dua jalan JK dan GH. Tentukan koordinat bagi lampu isyarat tersebut.
Penyelesaian:
(a)
$$
\begin{aligned}
\text { Titik tengah } E F & =\left(\frac{-7+3}{2}, \frac{-1+3}{2}\right) \\
& =\left(\frac{-4}{2}, \frac{2}{2}\right) \\
& =(-2,1)
\end{aligned}
$$
$$
\begin{aligned}
&\text { Gantikan nilai } x=-2 \text { dan } y=1 \text { ke dalam } y=-2 x+k\\
&\begin{aligned}
1 & =-2(-2)+k \\
1 & =4+k \\
k & =1-4 \\
& =-3
\end{aligned}
\end{aligned}
$$
(b)
$$
\begin{aligned}
&\begin{aligned}
& J K: \quad y=-2 x-3 \ldots \ldots . .(1) \\
& G H: y=2 x+17\ldots \ldots . .(2)
\end{aligned}\\
&\begin{aligned}
& \text { (l) tolak (2), } \\
& 0=-4 x-20 \\
& 4 x=-20 \\
& x=-\frac{20}{4} \\
&=-5
\end{aligned}
\end{aligned}
$$
Gantikan x = -5 dalam (1),
$$
\begin{aligned}
y & =-2(-5)-3 \\
& =10-3 \\
& =7
\end{aligned}
$$
Maka, koordinat bagi lampu isyarat ialah (-5, 7).