Soalan 1:
Penyelesaian:
(a)
$$
\begin{aligned}
P R^2 & =P Q^2+Q R^2 \\
P R^2 & =6^2+8^2 \\
& =100 \\
P R & =\sqrt{100} \\
& =10 \mathrm{~cm}
\end{aligned}
$$
(b)
$$
\begin{aligned}
S R^2 & =S P^2-P R^2 \\
S R^2 & =26^2-10^2 \\
& =576 \\
S R & =\sqrt{576} \\
& =24 \mathrm{~cm}
\end{aligned}
$$
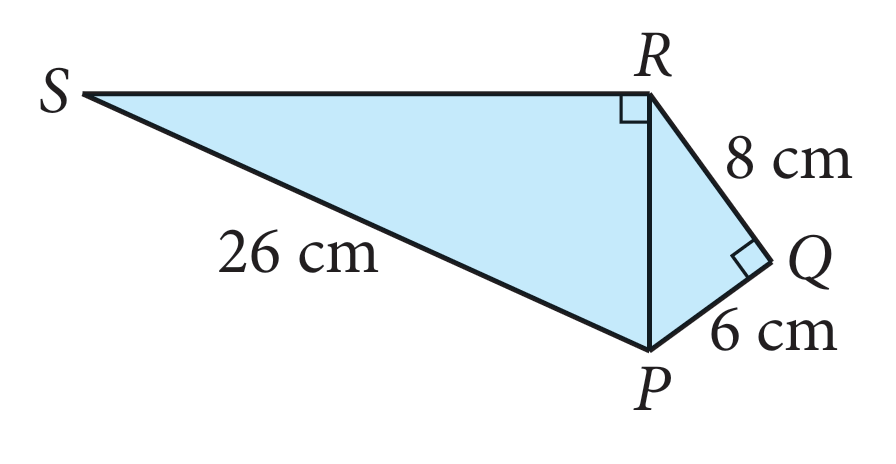
Dalam rajah di sebelah, hitung panjang
(a) PR
(b) SR
Penyelesaian:
(a)
$$
\begin{aligned}
P R^2 & =P Q^2+Q R^2 \\
P R^2 & =6^2+8^2 \\
& =100 \\
P R & =\sqrt{100} \\
& =10 \mathrm{~cm}
\end{aligned}
$$
(b)
$$
\begin{aligned}
S R^2 & =S P^2-P R^2 \\
S R^2 & =26^2-10^2 \\
& =576 \\
S R & =\sqrt{576} \\
& =24 \mathrm{~cm}
\end{aligned}
$$
Soalan 2:
Penyelesaian:
$$
\begin{aligned}
&\begin{aligned}
P Q^2 & =150^2+2^2 \\
& =22500+4 \\
& =22504 \\
P Q & =\sqrt{22504} \\
& =150.01 \mathrm{~m}
\end{aligned}\\
&\text { Maka, jarak sebenar adalah } 150.01 \text { m. }
\end{aligned}
$$
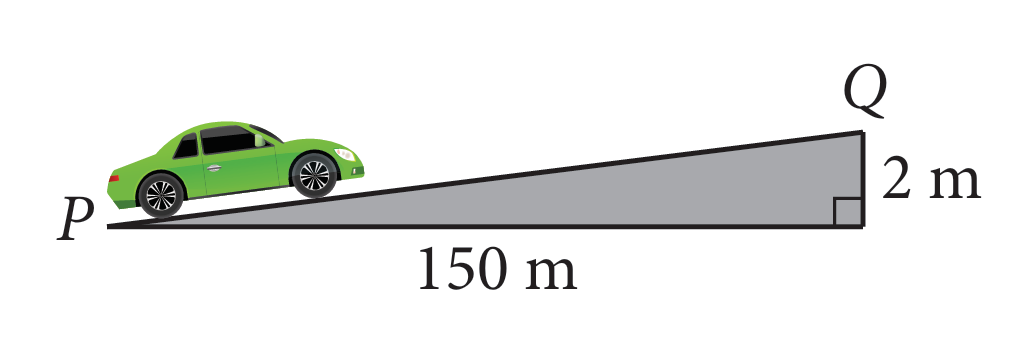
Sebuah kereta menaiki cerun jalan dari P ke Q. Apabila kereta itu sampai di Q, jarak mengufuk dan jarak menegak yang dilalui masing-masing ialah 150 m dan 2 m. Terangkan bagaimana anda menghitung jarak sebenar yang dilalui oleh kereta itu, betul kepada dua tempat perpuluhan.
Penyelesaian:
$$
\begin{aligned}
&\begin{aligned}
P Q^2 & =150^2+2^2 \\
& =22500+4 \\
& =22504 \\
P Q & =\sqrt{22504} \\
& =150.01 \mathrm{~m}
\end{aligned}\\
&\text { Maka, jarak sebenar adalah } 150.01 \text { m. }
\end{aligned}
$$
Soalan 3:
Penyelesaian:
(a)
$$
\begin{aligned}
Q S^2 & =Q R^2+R S^2 \\
& =9^2+12^2 \\
& =81+144 \\
& =225 \\
Q S & =\sqrt{225} \\
& =15 \mathrm{~cm}
\end{aligned}
$$
(b)
$$
\begin{aligned}
&\begin{aligned}
\text { Sisi terpanjang } & =17 \mathrm{~cm} \\
17^2 & =289 \\
8^2+15^2 & =64+225 \\
& =289 \\
8^2+15^2 & =17^2
\end{aligned}\\
&\text { Ya, } P Q S \text { adalah sebuah segi tiga bersudut tegak. }
\end{aligned}
$$
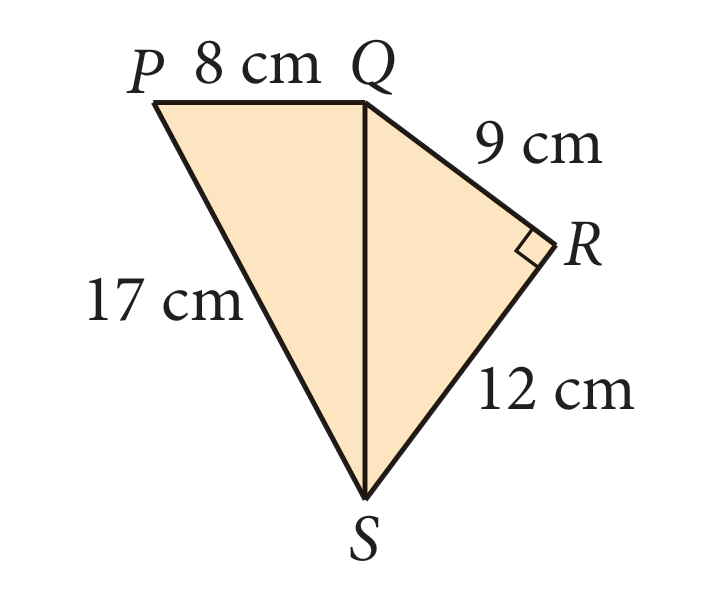
Berdasarkan rajah di sebelah,
(a) hitung panjang QS.
(b) terangkan sama ada PQS ialah sebuah segi tiga bersudut tegak atau bukan.
Penyelesaian:
(a)
$$
\begin{aligned}
Q S^2 & =Q R^2+R S^2 \\
& =9^2+12^2 \\
& =81+144 \\
& =225 \\
Q S & =\sqrt{225} \\
& =15 \mathrm{~cm}
\end{aligned}
$$
(b)
$$
\begin{aligned}
&\begin{aligned}
\text { Sisi terpanjang } & =17 \mathrm{~cm} \\
17^2 & =289 \\
8^2+15^2 & =64+225 \\
& =289 \\
8^2+15^2 & =17^2
\end{aligned}\\
&\text { Ya, } P Q S \text { adalah sebuah segi tiga bersudut tegak. }
\end{aligned}
$$
Soalan 4:
Penyelesaian:
$$
\begin{aligned}
Q S & =P Q=P T=T S=10 \mathrm{~cm} \\
S R^2 & =Q S^2-Q R^2 \\
& =10^2-8^2 \\
& =36 \\
S R & =\sqrt{36} \\
& =6 \mathrm{~cm}
\end{aligned}
$$
$$
\begin{aligned}
\text { Luas trapizium, } P Q R T & =\frac{1}{2} \times[10+(10+6)] \times 8 \\
& =104 \mathrm{~cm}^2
\end{aligned}
$$
$$
\text { Maka, luas seluruh rajah adalah } 104 \mathrm{~cm}^2 \text {. }
$$
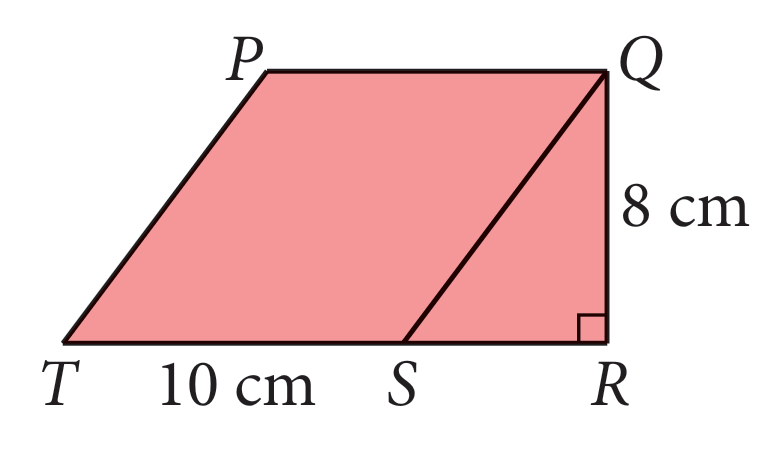
Dalam rajah di sebelah, PQST ialah sebuah rombus dan TSR ialah garis lurus. Hitung luas seluruh rajah.
Penyelesaian:
$$
\begin{aligned}
Q S & =P Q=P T=T S=10 \mathrm{~cm} \\
S R^2 & =Q S^2-Q R^2 \\
& =10^2-8^2 \\
& =36 \\
S R & =\sqrt{36} \\
& =6 \mathrm{~cm}
\end{aligned}
$$
$$
\begin{aligned}
\text { Luas trapizium, } P Q R T & =\frac{1}{2} \times[10+(10+6)] \times 8 \\
& =104 \mathrm{~cm}^2
\end{aligned}
$$
$$
\text { Maka, luas seluruh rajah adalah } 104 \mathrm{~cm}^2 \text {. }
$$