Soalan 1:
Penyelesaian:
$$
\begin{aligned}
&\begin{aligned}
\text { Sisi terpanjang } & =2.5 \mathrm{~m} \\
2.5^2 & =6.25 \\
1.5^2+2^2 & =2.25+4 \\
& =6.25 \\
1.5^2+2^2 & =2.5^2
\end{aligned}\\
&\text { Maka, dinding itu adalah tegak. }
\end{aligned}
$$
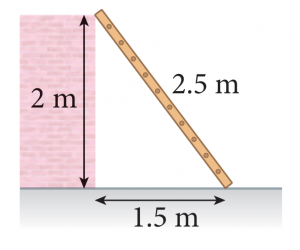
Sebuah tangga dengan panjang 2.5 m bersandar pada dinding sebuah bangunan. Jarak di antara kaki tangga dengan dinding itu ialah 1.5 m.
Terangkan bagaimana anda menentukan sama ada dinding itu tegak atau tidak.123
Penyelesaian:
$$
\begin{aligned}
&\begin{aligned}
\text { Sisi terpanjang } & =2.5 \mathrm{~m} \\
2.5^2 & =6.25 \\
1.5^2+2^2 & =2.25+4 \\
& =6.25 \\
1.5^2+2^2 & =2.5^2
\end{aligned}\\
&\text { Maka, dinding itu adalah tegak. }
\end{aligned}
$$
Soalan 2:
Penyelesaian:
$$
\begin{aligned}
& 6^2+8^2=36+64 \\
&=100 \\
& 10^2=100 \\
& 6^2+8^2=10^2 \\
& \text { Maka } \angle P Q S=90^{\circ}
\end{aligned}
$$
$$
\begin{aligned}
&\begin{aligned}
\angle R Q S & =180^{\circ}-65^{\circ}-45^{\circ} \\
& =70^{\circ}
\end{aligned}\\
&\begin{aligned}
\angle P Q R & =\angle P Q S+\angle R Q S \\
& =90^{\circ}+70^{\circ} \\
& =160^{\circ}
\end{aligned}
\end{aligned}
$$
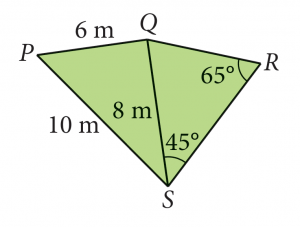
Dalam rajah di sebelah, cari ∠PQR.
Penyelesaian:
$$
\begin{aligned}
& 6^2+8^2=36+64 \\
&=100 \\
& 10^2=100 \\
& 6^2+8^2=10^2 \\
& \text { Maka } \angle P Q S=90^{\circ}
\end{aligned}
$$
$$
\begin{aligned}
&\begin{aligned}
\angle R Q S & =180^{\circ}-65^{\circ}-45^{\circ} \\
& =70^{\circ}
\end{aligned}\\
&\begin{aligned}
\angle P Q R & =\angle P Q S+\angle R Q S \\
& =90^{\circ}+70^{\circ} \\
& =160^{\circ}
\end{aligned}
\end{aligned}
$$