Soalan 1:
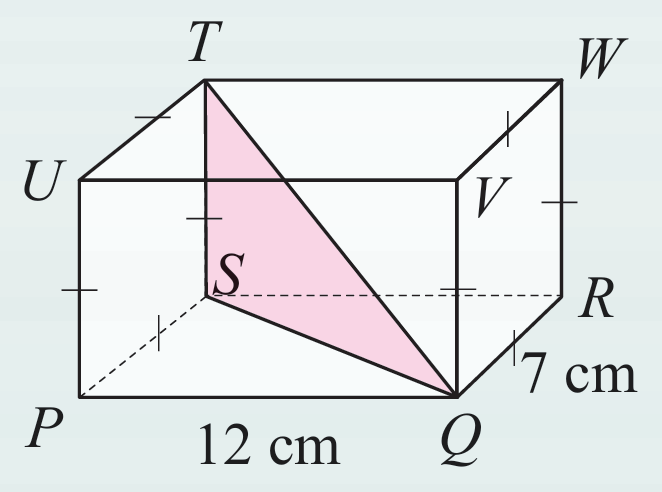
Rajah di sebelah menunjukkan sebuah kuboid PQRSTUVW. QRWV dan PSTU ialah segi empat sama. Diberi bahawa PQ = 12 cm dan QR = 7 cm. Hitung
(a) tan ∠PQS
(b) panjang TQ, dalam cm, betul kepada empat angka bererti
(c) nilai ∠SQT, dalam darjah dan minit
Penyelesaian:
(a)
$$ \begin{aligned} \tan & =\frac{\text { sisi bertentangan }}{\text { sisi bersebelahan }} \\ \tan \angle P Q S & =\frac{P S}{P Q} \\ & =\frac{7}{12} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Guna teorem Pythagoras, }\\ &\begin{aligned} Q S & =\sqrt{P S^2+P Q^2} \\ & =\sqrt{7^2+12^2} \\ & =\sqrt{193} \\ & =13.89 \mathrm{~cm} \\ T Q & =\sqrt{T S^2+S Q^2} \\ & =\sqrt{7^2+13.89^2} \\ & =\sqrt{241.93} \\ T Q & =15.55 \mathrm{~cm} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} \tan \angle S Q T & =\frac{7}{13.89} \\ \angle S Q T & =\tan ^{-1}\left(\frac{7}{13.89}\right) \\ & =26^{\circ} 45^{\prime} \end{aligned} $$

Rajah di sebelah menunjukkan sebuah kuboid PQRSTUVW. QRWV dan PSTU ialah segi empat sama. Diberi bahawa PQ = 12 cm dan QR = 7 cm. Hitung
(a) tan ∠PQS
(b) panjang TQ, dalam cm, betul kepada empat angka bererti
(c) nilai ∠SQT, dalam darjah dan minit
Penyelesaian:
(a)
$$ \begin{aligned} \tan & =\frac{\text { sisi bertentangan }}{\text { sisi bersebelahan }} \\ \tan \angle P Q S & =\frac{P S}{P Q} \\ & =\frac{7}{12} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Guna teorem Pythagoras, }\\ &\begin{aligned} Q S & =\sqrt{P S^2+P Q^2} \\ & =\sqrt{7^2+12^2} \\ & =\sqrt{193} \\ & =13.89 \mathrm{~cm} \\ T Q & =\sqrt{T S^2+S Q^2} \\ & =\sqrt{7^2+13.89^2} \\ & =\sqrt{241.93} \\ T Q & =15.55 \mathrm{~cm} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} \tan \angle S Q T & =\frac{7}{13.89} \\ \angle S Q T & =\tan ^{-1}\left(\frac{7}{13.89}\right) \\ & =26^{\circ} 45^{\prime} \end{aligned} $$
Soalan 2:
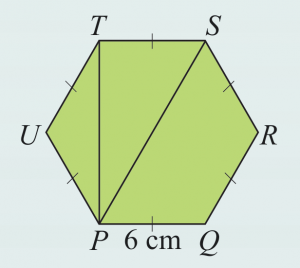
Rajah di sebelah menunjukkan sebuah heksagon sekata PQRSTU bersisi 6 cm. Hitung
(a) ∠PTS
(b) ∠TPS
(c) panjang TP, dalam cm, betul kepada tiga angka bererti
(d) nisbah luas ∆PTU kepada luas ∆PTS
Penyelesaian:
(a)
$$ \begin{aligned} \text { Sudut pedalaman poligon sekata } & =\frac{(n-2) \times 180^{\circ}}{n} \\ \text { Sudut pedalaman heksagon sekata } & =\frac{(6-2) \times 180^{\circ}}{6} \\ & =\frac{4 \times 180^{\circ}}{6} \\ & =120^{\circ} \end{aligned} $$
$$ \begin{aligned} &\triangle P U T \text { ialah segi tiga sama kaki, }\\ &\begin{aligned} \angle U T P=\angle U P T & =\left(180^{\circ}-120^{\circ}\right) \times \frac{1}{2} \\ & =30^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \angle U T P+\angle P T S & =\angle U T S \\ 30^{\circ}+\angle P T S & =120^{\circ} \\ \angle P T S & =120^{\circ}-30^{\circ} \\ & =90^{\circ} \end{aligned} $$
(b)
PS ialah paksi simetri bagi heksagon ini.
PS ialah pembahagi dua sama ∠RST.
\begin{aligned} \angle P S T & =\frac{1}{2} \angle R S T \\ & =\frac{1}{2} \times 120^{\circ} \\ & =60^{\circ} \end{aligned}
$$ \begin{aligned} \angle P T S+\angle T P S+\angle P S T & =180^{\circ} \\ 90^{\circ}+\angle T P S+60^{\circ} & =180^{\circ} \\ \angle T P S & =180^{\circ}-90^{\circ}-60^{\circ} \\ & =30^{\circ} \end{aligned} $$
(c)
$$ \begin{aligned} \tan \angle T P S & =\frac{T S}{T P} \\ \tan 30^{\circ} & =\frac{6}{T P} \\ T P & =\frac{6}{\tan 30^{\circ}} \\ & =10.4 \mathrm{~cm} \end{aligned} $$
(d)
$$ \begin{aligned} &\text { Tinggi }\\ &\begin{aligned} \triangle P T U & =\sqrt{U T^2-(T P \div 2)^2} \\ & =\sqrt{6^2-(10.4 \div 2)^2} \\ & =\sqrt{36-27.04} \\ & =2.993 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \text { Luas } \begin{aligned} \triangle P T U & =\frac{1}{2} \times 2.993 \times 10.4 \\ & =15.6 \mathrm{~cm}^2 \end{aligned} $$
$$ \text { Luas } \begin{aligned} \triangle P T S & =\frac{1}{2} \times 6 \times 10.4 \\ & =31.2 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{aligned} &\text { Maka, nisbah luas } \triangle P T U \text { kepada luas } \triangle P T S\\ &\begin{aligned} & =15.6: 31.2 \\ & =\frac{15.6}{15.6}: \frac{31.2}{15.6} \\ & =1: 2 \end{aligned} \end{aligned} $$

Rajah di sebelah menunjukkan sebuah heksagon sekata PQRSTU bersisi 6 cm. Hitung
(a) ∠PTS
(b) ∠TPS
(c) panjang TP, dalam cm, betul kepada tiga angka bererti
(d) nisbah luas ∆PTU kepada luas ∆PTS
Penyelesaian:
(a)
$$ \begin{aligned} \text { Sudut pedalaman poligon sekata } & =\frac{(n-2) \times 180^{\circ}}{n} \\ \text { Sudut pedalaman heksagon sekata } & =\frac{(6-2) \times 180^{\circ}}{6} \\ & =\frac{4 \times 180^{\circ}}{6} \\ & =120^{\circ} \end{aligned} $$
$$ \begin{aligned} &\triangle P U T \text { ialah segi tiga sama kaki, }\\ &\begin{aligned} \angle U T P=\angle U P T & =\left(180^{\circ}-120^{\circ}\right) \times \frac{1}{2} \\ & =30^{\circ} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \angle U T P+\angle P T S & =\angle U T S \\ 30^{\circ}+\angle P T S & =120^{\circ} \\ \angle P T S & =120^{\circ}-30^{\circ} \\ & =90^{\circ} \end{aligned} $$
(b)
PS ialah paksi simetri bagi heksagon ini.
PS ialah pembahagi dua sama ∠RST.
\begin{aligned} \angle P S T & =\frac{1}{2} \angle R S T \\ & =\frac{1}{2} \times 120^{\circ} \\ & =60^{\circ} \end{aligned}
$$ \begin{aligned} \angle P T S+\angle T P S+\angle P S T & =180^{\circ} \\ 90^{\circ}+\angle T P S+60^{\circ} & =180^{\circ} \\ \angle T P S & =180^{\circ}-90^{\circ}-60^{\circ} \\ & =30^{\circ} \end{aligned} $$
(c)
$$ \begin{aligned} \tan \angle T P S & =\frac{T S}{T P} \\ \tan 30^{\circ} & =\frac{6}{T P} \\ T P & =\frac{6}{\tan 30^{\circ}} \\ & =10.4 \mathrm{~cm} \end{aligned} $$
(d)
$$ \begin{aligned} &\text { Tinggi }\\ &\begin{aligned} \triangle P T U & =\sqrt{U T^2-(T P \div 2)^2} \\ & =\sqrt{6^2-(10.4 \div 2)^2} \\ & =\sqrt{36-27.04} \\ & =2.993 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \text { Luas } \begin{aligned} \triangle P T U & =\frac{1}{2} \times 2.993 \times 10.4 \\ & =15.6 \mathrm{~cm}^2 \end{aligned} $$
$$ \text { Luas } \begin{aligned} \triangle P T S & =\frac{1}{2} \times 6 \times 10.4 \\ & =31.2 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{aligned} &\text { Maka, nisbah luas } \triangle P T U \text { kepada luas } \triangle P T S\\ &\begin{aligned} & =15.6: 31.2 \\ & =\frac{15.6}{15.6}: \frac{31.2}{15.6} \\ & =1: 2 \end{aligned} \end{aligned} $$
Soalan 3:
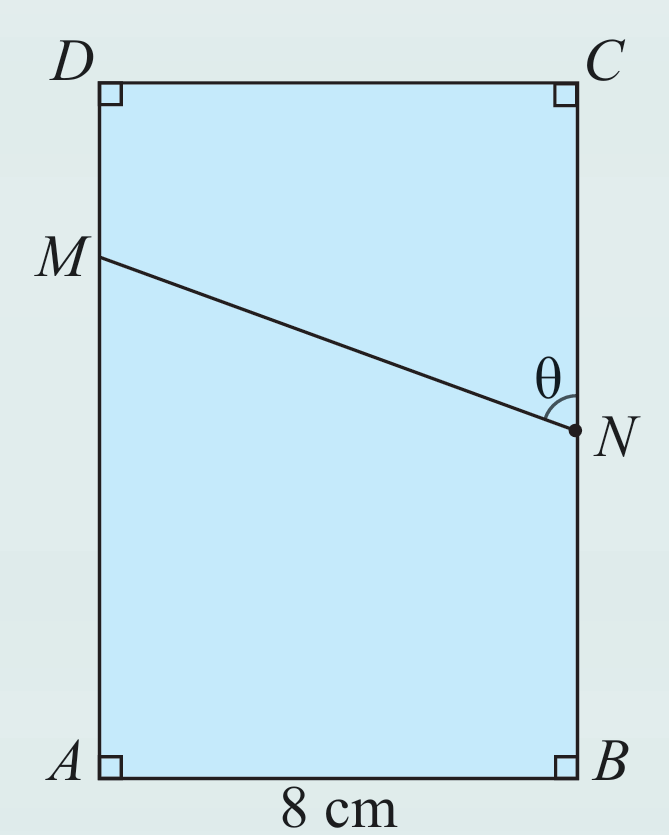
Rajah di sebelah menunjukkan sebuah segi empat tepat ABCD. Diberi bahawa AB = 8 cm, BC = 2 AB dan N ialah titik tengah BC.
(a) Jika MD = 1/4 AD, hitungkan panjang MN, dalam cm. Nyatakan jawapan anda dalam bentuk surd
(b) Hitung nilai θ, dalam darjah dan minit
(c) Shahril menyatakan bahawa nisbah luas trapezium CDMN kepada luas trapezium ABNM ialah 1 : 2. Adakah pernyataan Shahril benar? Nyatakan alasan untuk jawapan anda.
Penyelesaian:
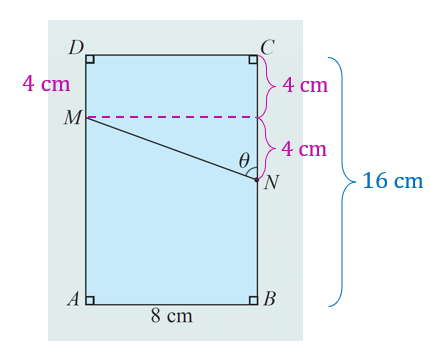
(a)
$$ \begin{aligned} B C & =2 A B \\ & =2(8) \\ & =16 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} \text { Diberi } M D & =\frac{1}{4} A D \\ & =\frac{1}{4} \times 16 \\ & =4 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} &\text { Guna teorem Pythagoras, }\\ &\begin{aligned} M N & =\sqrt{8^2+4^2} \\ & =\sqrt{80} \\ & =\sqrt{16 \times 5} \\ & =4 \sqrt{5} \mathrm{~cm} \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} \tan \theta & =\frac{8}{4} \\ & =2 \\ \theta & =\tan ^{-1}(2) \\ & =63^{\circ} 26^{\prime} \end{aligned} $$
(c)
$$ \begin{aligned} \text { Luas trapezium } C D M N & =\frac{1}{2}(D M+C N)(C D) \\ & =\frac{1}{2}(4+8)(8) \\ & =48 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{aligned} \text { Luas trapezium } A B N M & =\frac{1}{2}(A M+B N)(A B) \\ & =\frac{1}{2}(12+8)(8) \\ & =80 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{aligned} &\text { Nisbah luas trapezium CDMN kepada luas trapezium } A B N M\\ &\begin{aligned} & =48: 80 \\ & =3: 5 \end{aligned} \end{aligned} $$
Pernyataan Shahril tidak benar, nisbah sebenar adalah 3 : 5.

Rajah di sebelah menunjukkan sebuah segi empat tepat ABCD. Diberi bahawa AB = 8 cm, BC = 2 AB dan N ialah titik tengah BC.
(a) Jika MD = 1/4 AD, hitungkan panjang MN, dalam cm. Nyatakan jawapan anda dalam bentuk surd
(b) Hitung nilai θ, dalam darjah dan minit
(c) Shahril menyatakan bahawa nisbah luas trapezium CDMN kepada luas trapezium ABNM ialah 1 : 2. Adakah pernyataan Shahril benar? Nyatakan alasan untuk jawapan anda.
Penyelesaian:

(a)
$$ \begin{aligned} B C & =2 A B \\ & =2(8) \\ & =16 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} \text { Diberi } M D & =\frac{1}{4} A D \\ & =\frac{1}{4} \times 16 \\ & =4 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} &\text { Guna teorem Pythagoras, }\\ &\begin{aligned} M N & =\sqrt{8^2+4^2} \\ & =\sqrt{80} \\ & =\sqrt{16 \times 5} \\ & =4 \sqrt{5} \mathrm{~cm} \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} \tan \theta & =\frac{8}{4} \\ & =2 \\ \theta & =\tan ^{-1}(2) \\ & =63^{\circ} 26^{\prime} \end{aligned} $$
(c)
$$ \begin{aligned} \text { Luas trapezium } C D M N & =\frac{1}{2}(D M+C N)(C D) \\ & =\frac{1}{2}(4+8)(8) \\ & =48 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{aligned} \text { Luas trapezium } A B N M & =\frac{1}{2}(A M+B N)(A B) \\ & =\frac{1}{2}(12+8)(8) \\ & =80 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{aligned} &\text { Nisbah luas trapezium CDMN kepada luas trapezium } A B N M\\ &\begin{aligned} & =48: 80 \\ & =3: 5 \end{aligned} \end{aligned} $$
Pernyataan Shahril tidak benar, nisbah sebenar adalah 3 : 5.