Soalan 6:
Titik tengah bagi segi empat tepat dalam rajah di bawah adalah di asalan.
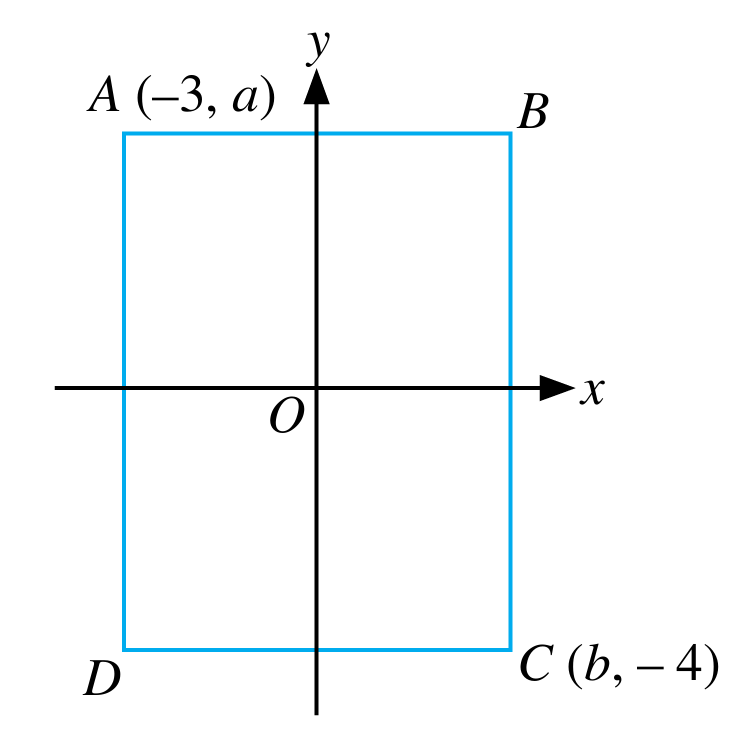
Tentukan
(a) nilai a dan b.
(b) jarak bagi garis lurus BC.
(c) koordinat B.
Penyelesaian:
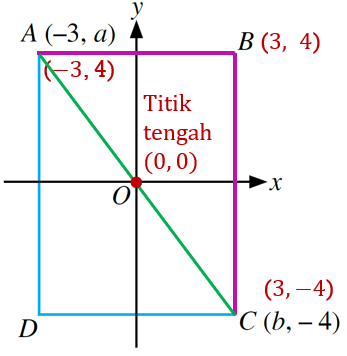
(a)
$$ \begin{aligned} (0,0)=\left(\frac{-3+b}{2},\right. & \left.\frac{a+(-4)}{2}\right) \\ \frac{-3+b}{2} & =0 \\ -3+b & =0 \\ b & =3 \\ \frac{a-4}{2} & =0 \\ a-4 & =0 \\ a & =4 \end{aligned} $$
(b)
Jarak BC = 4 – (-4)
= 8 unit
(c)
Dari graf, B (3, 4)
Titik tengah bagi segi empat tepat dalam rajah di bawah adalah di asalan.

Tentukan
(a) nilai a dan b.
(b) jarak bagi garis lurus BC.
(c) koordinat B.
Penyelesaian:

(a)
$$ \begin{aligned} (0,0)=\left(\frac{-3+b}{2},\right. & \left.\frac{a+(-4)}{2}\right) \\ \frac{-3+b}{2} & =0 \\ -3+b & =0 \\ b & =3 \\ \frac{a-4}{2} & =0 \\ a-4 & =0 \\ a & =4 \end{aligned} $$
(b)
Jarak BC = 4 – (-4)
= 8 unit
(c)
Dari graf, B (3, 4)
Soalan 7:
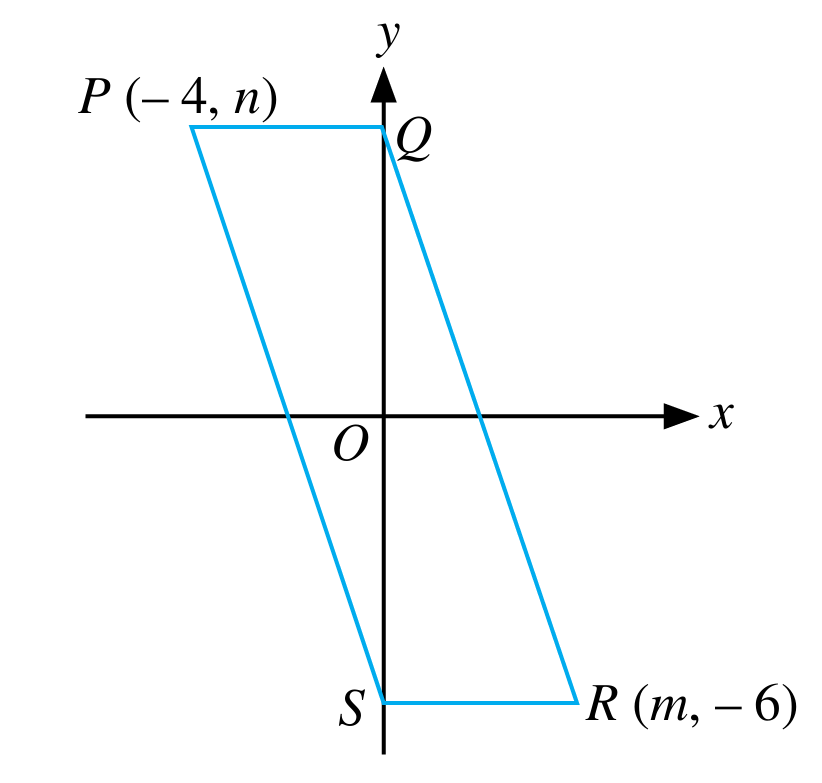
Titik asalan ialah titik tengah bagi tinggi segi empat selari. Hitung
(a) nilai m dan n.
(b) titik tengah bagi garis lurus PQ.
(c) titik tengah bagi garis lurus SR.
Penyelesaian:
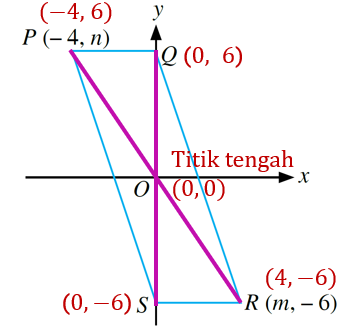
(a)
$$ \begin{aligned} (0,0)= & \left(\frac{-4+m}{2}, \frac{n+(-6)}{2}\right) \\ -\frac{4+m}{2} & =0 \\ -4+m & =0 \\ m & =4 \\ \frac{n-6}{2} & =0 \\ n-6 & =0 \\ n & =6 \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Titik tengah } P Q=\left(\frac{-4+0}{2}, \frac{6+6}{2}\right)\\ &=(-2,6) \end{aligned} $$
(c)
$$ \text { Titik tengah } \begin{aligned} S R & =\left(\frac{0+4}{2}, \frac{-6+(-6)}{2}\right) \\ & =(2,-6) \end{aligned} $$

Titik asalan ialah titik tengah bagi tinggi segi empat selari. Hitung
(a) nilai m dan n.
(b) titik tengah bagi garis lurus PQ.
(c) titik tengah bagi garis lurus SR.
Penyelesaian:

(a)
$$ \begin{aligned} (0,0)= & \left(\frac{-4+m}{2}, \frac{n+(-6)}{2}\right) \\ -\frac{4+m}{2} & =0 \\ -4+m & =0 \\ m & =4 \\ \frac{n-6}{2} & =0 \\ n-6 & =0 \\ n & =6 \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Titik tengah } P Q=\left(\frac{-4+0}{2}, \frac{6+6}{2}\right)\\ &=(-2,6) \end{aligned} $$
(c)
$$ \text { Titik tengah } \begin{aligned} S R & =\left(\frac{0+4}{2}, \frac{-6+(-6)}{2}\right) \\ & =(2,-6) \end{aligned} $$
Soalan 8:
Diberi garis lurus AB = BD dengan D (–1, 3) dan B (1, 1). Hitung koordinat bagi titik A.
Penyelesaian:
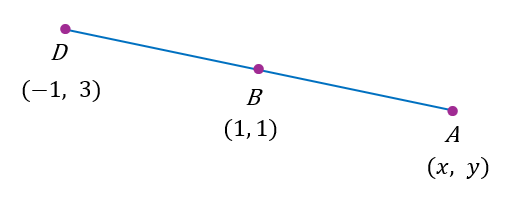
$$ \begin{aligned} (1,1) & =\left(\frac{x+(-1)}{2}, \frac{y+3}{2}\right) \\ \frac{x-1}{2} & =1 \\ x-1 & =2 \\ x & =3 \end{aligned} $$
$$ \begin{aligned} \frac{y+3}{2} & =1 \\ y+3 & =2 \\ y & =-1 \\ \therefore \mathrm{~A}(3, & -1) \end{aligned} $$
Diberi garis lurus AB = BD dengan D (–1, 3) dan B (1, 1). Hitung koordinat bagi titik A.
Penyelesaian:

$$ \begin{aligned} (1,1) & =\left(\frac{x+(-1)}{2}, \frac{y+3}{2}\right) \\ \frac{x-1}{2} & =1 \\ x-1 & =2 \\ x & =3 \end{aligned} $$
$$ \begin{aligned} \frac{y+3}{2} & =1 \\ y+3 & =2 \\ y & =-1 \\ \therefore \mathrm{~A}(3, & -1) \end{aligned} $$
Soalan 9:
Garisan yang menyambungkan titik (–8, 3) dan (s, 3) mempunyai titik tengah (0, u). Hitung nilai s dan u.
Penyelesaian:
$$ \begin{aligned} (0, u) & =\left(\frac{-8+s}{2}, \frac{3+3}{2}\right) \\ \frac{-8+s}{2} & =0 \\ -8+s & =0 \\ s & =8 \\ \frac{3+3}{2} & =u \\ u & =3 \end{aligned} $$
Garisan yang menyambungkan titik (–8, 3) dan (s, 3) mempunyai titik tengah (0, u). Hitung nilai s dan u.
Penyelesaian:
$$ \begin{aligned} (0, u) & =\left(\frac{-8+s}{2}, \frac{3+3}{2}\right) \\ \frac{-8+s}{2} & =0 \\ -8+s & =0 \\ s & =8 \\ \frac{3+3}{2} & =u \\ u & =3 \end{aligned} $$
Soalan 10:
Garis AB selari dengan paksi-x dengan titik A (3, a) dan titik tengah bagi garis lurus AB ialah (5, 1).
Hitung
(a) nilai a.
(b) koordinat B.
Penyelesaian:
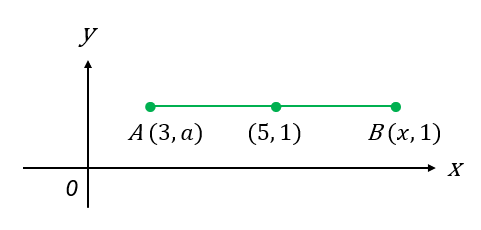
(a)
Diberi garis AB adalah selari dengan paksi x, maka, semua titik yang berada pada garis AB mempunyai koordinat y yang sama.
Oleh itu, a = 1
(b)
$$ \begin{aligned} & \begin{aligned} (5,1) & =\left(\frac{3+x}{2}, \frac{1+1}{2}\right) \\ \frac{3+x}{2} & =5 \\ 3+x & =10 \\ x & =7 \end{aligned} \\ & \text { Koordinat } B=(7,1) \end{aligned} $$
Garis AB selari dengan paksi-x dengan titik A (3, a) dan titik tengah bagi garis lurus AB ialah (5, 1).
Hitung
(a) nilai a.
(b) koordinat B.
Penyelesaian:

(a)
Diberi garis AB adalah selari dengan paksi x, maka, semua titik yang berada pada garis AB mempunyai koordinat y yang sama.
Oleh itu, a = 1
(b)
$$ \begin{aligned} & \begin{aligned} (5,1) & =\left(\frac{3+x}{2}, \frac{1+1}{2}\right) \\ \frac{3+x}{2} & =5 \\ 3+x & =10 \\ x & =7 \end{aligned} \\ & \text { Koordinat } B=(7,1) \end{aligned} $$