Soalan 2:
Sebuah botol air berbentuk silinder dengan ketinggian 20 cm dan diameter 5.5 cm diisi air hingga penuh. Vincent ingin memindahkan air di dalam botol itu ke dalam sebuah bekas berbentuk kubus. Nyatakan panjang minimum sisi kubus tersebut.
Penyelesaian:
$$ \begin{aligned} \text { Jejari } & =5.5 \mathrm{~cm} \div 2 \\ & =2.75 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} \text { Isi padu silinder } & =\text { Luas keratan rentas } \times \text { Tinggi } \\ & =\pi j^2 t \\ & =\left(\frac{22}{7} \times 2.75 \mathrm{~cm} \times 2.75 \mathrm{~cm}\right) \times 20 \mathrm{~cm} \\ & =475.36 \mathrm{~cm}^3 \end{aligned} $$
$$ \begin{aligned} &\begin{aligned} \text { Katakan sisi kubus } & =y \\ \text { Isi padu kubus } & =y \times y \times y \\ y^3 & =475.36 \\ y & =\sqrt[3]{475.36} \\ y & \approx 7.80 \end{aligned}\\ &\text { Maka, panjang minimum sisi kubus }=8 \mathrm{~cm} \text {. } \end{aligned} $$
Sebuah botol air berbentuk silinder dengan ketinggian 20 cm dan diameter 5.5 cm diisi air hingga penuh. Vincent ingin memindahkan air di dalam botol itu ke dalam sebuah bekas berbentuk kubus. Nyatakan panjang minimum sisi kubus tersebut.
Penyelesaian:
$$ \begin{aligned} \text { Jejari } & =5.5 \mathrm{~cm} \div 2 \\ & =2.75 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} \text { Isi padu silinder } & =\text { Luas keratan rentas } \times \text { Tinggi } \\ & =\pi j^2 t \\ & =\left(\frac{22}{7} \times 2.75 \mathrm{~cm} \times 2.75 \mathrm{~cm}\right) \times 20 \mathrm{~cm} \\ & =475.36 \mathrm{~cm}^3 \end{aligned} $$
$$ \begin{aligned} &\begin{aligned} \text { Katakan sisi kubus } & =y \\ \text { Isi padu kubus } & =y \times y \times y \\ y^3 & =475.36 \\ y & =\sqrt[3]{475.36} \\ y & \approx 7.80 \end{aligned}\\ &\text { Maka, panjang minimum sisi kubus }=8 \mathrm{~cm} \text {. } \end{aligned} $$
Soalan 3:
Diberi isi padu gabungan bentuk geometri tiga dimensi berikut, hitung nilai t.
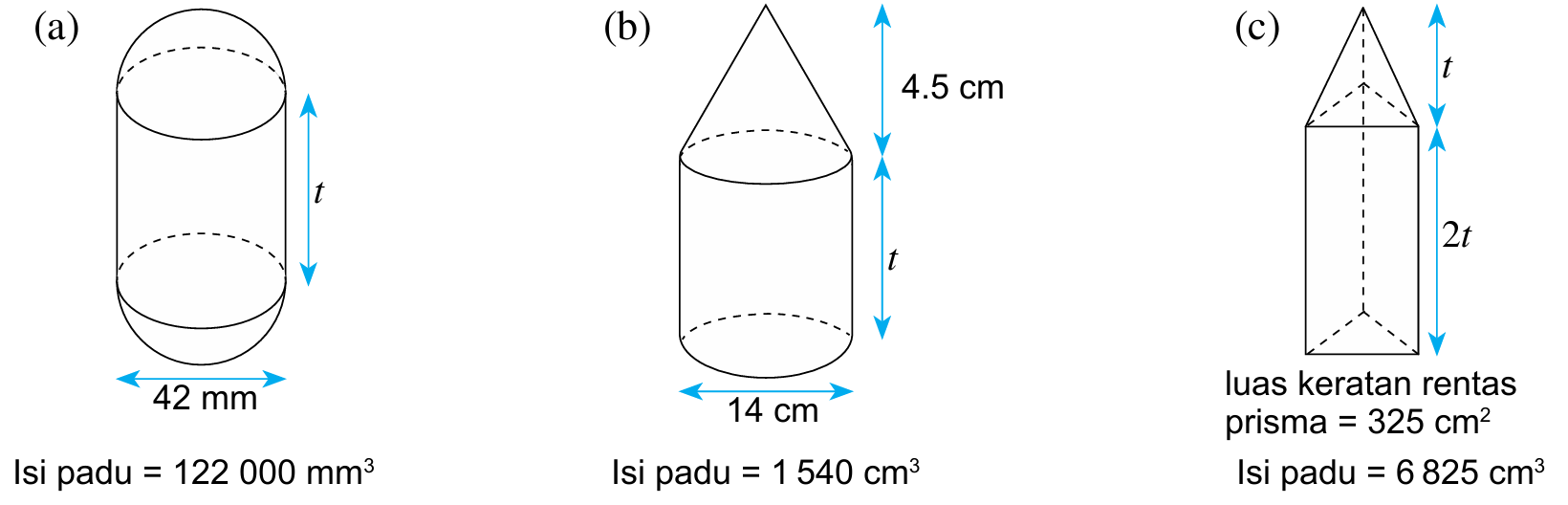
Penyelesaian:
(a)
$$ \begin{aligned} \text { Jejari } & =42 \mathrm{~mm} \div 2 \\ & =21 \mathrm{~mm} \end{aligned} $$
$$ \begin{aligned} &\text { Isi padu gabungan = Isi padu silinder + isi padu sfera }\\ &\begin{aligned} 122000 & =\pi j^2 t+\frac{4}{3} \pi j^3 \\ 122000 & =\left(\frac{22}{7} \times 21^2 \times t\right)+\left(\frac{4}{3} \times \frac{22}{7} \times 21^3\right) \\ 122000 & =1386 t+38808 \\ 1386 t & =83192 \\ t & =60 \mathrm{~mm} \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} \text { Lejari } & =14 \mathrm{~cm} \div 2 \\ & =7 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} &\text { Isi padu gabungan = Isi padu silinder + isi padu kon }\\ &\begin{aligned} 1540 & =\pi j^2 t+\frac{1}{3} \pi j^2 t \\ 1540 & =\left(\frac{22}{7} \times 7^2 \times t\right)+\left(\frac{1}{3} \times \frac{22}{7} \times 7^2 \times 4.5\right) \\ 1540 & =154 t+231 \\ 154 t & =1309 \\ t & =8.5 \mathrm{~cm} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} \text { Katakan tinggi prisma } & =h_1 \\ \text { Tinggi piramid } & =h_2 \\ \text { Luas keratan rentas } & =A \end{aligned} $$
$$ \begin{aligned} \text { Isi padu gabungan } & =\text { isi padu prisma }+ \text { Isi padu piramid } \\ 6825 & =A h_1+1 / 3 A h_2 \\ 6825 & =(325 \times 2 t)+\left(\frac{1}{3} \times 325 \times t\right) \\ 21 & =2 t+\frac{1}{3} t \\ 21 & =\frac{7}{3} t \\ t & =\frac{3 \times 21}{7} \\ & =9 \mathrm{~cm} \end{aligned} $$
Diberi isi padu gabungan bentuk geometri tiga dimensi berikut, hitung nilai t.

Penyelesaian:
(a)
$$ \begin{aligned} \text { Jejari } & =42 \mathrm{~mm} \div 2 \\ & =21 \mathrm{~mm} \end{aligned} $$
$$ \begin{aligned} &\text { Isi padu gabungan = Isi padu silinder + isi padu sfera }\\ &\begin{aligned} 122000 & =\pi j^2 t+\frac{4}{3} \pi j^3 \\ 122000 & =\left(\frac{22}{7} \times 21^2 \times t\right)+\left(\frac{4}{3} \times \frac{22}{7} \times 21^3\right) \\ 122000 & =1386 t+38808 \\ 1386 t & =83192 \\ t & =60 \mathrm{~mm} \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} \text { Lejari } & =14 \mathrm{~cm} \div 2 \\ & =7 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} &\text { Isi padu gabungan = Isi padu silinder + isi padu kon }\\ &\begin{aligned} 1540 & =\pi j^2 t+\frac{1}{3} \pi j^2 t \\ 1540 & =\left(\frac{22}{7} \times 7^2 \times t\right)+\left(\frac{1}{3} \times \frac{22}{7} \times 7^2 \times 4.5\right) \\ 1540 & =154 t+231 \\ 154 t & =1309 \\ t & =8.5 \mathrm{~cm} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} \text { Katakan tinggi prisma } & =h_1 \\ \text { Tinggi piramid } & =h_2 \\ \text { Luas keratan rentas } & =A \end{aligned} $$
$$ \begin{aligned} \text { Isi padu gabungan } & =\text { isi padu prisma }+ \text { Isi padu piramid } \\ 6825 & =A h_1+1 / 3 A h_2 \\ 6825 & =(325 \times 2 t)+\left(\frac{1}{3} \times 325 \times t\right) \\ 21 & =2 t+\frac{1}{3} t \\ 21 & =\frac{7}{3} t \\ t & =\frac{3 \times 21}{7} \\ & =9 \mathrm{~cm} \end{aligned} $$
Soalan 4:
Perhatikan rajah di bawah. Diameter hemisfera tersebut ialah 22 cm, hitung
(a) isi padu gabungan bentuk geometri tiga dimensi di bawah.
(b) jumlah bilangan guli dengan isi padu 343 mm3 yang boleh dimasukkan ke dalam bekas tersebut.
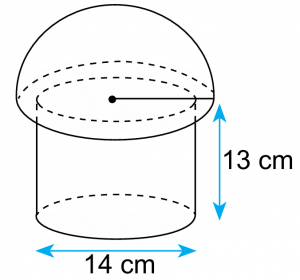
Penyelesaian:
(a)
$$ \begin{aligned} \text { Jejari hemisfera } & =22 \mathrm{~cm} \div 2 \\ & =11 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} \text { jejari silinder } & =14 \mathrm{~cm} \div 2 \\ & =7 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} \text { Isi padu gabungan } & =\text { Isi padu hemisfera }+ \text { isi padu silinder } \\ & =\pi j^2 t+\frac{2}{3} \pi j^3 \\ & =\left(\frac{22}{7} \times 7^2 \times 13\right)+\left(\frac{2}{3} \times \frac{22}{7} \times 11^3\right) \\ & =2002+2788.76 \\ & =4790.76 \mathrm{~cm}^3 \end{aligned} $$
(b)
$$ \begin{aligned} \text { Isipadu sebiji guli } & =343 \mathrm{~mm}^3 \\ & =0.343 \mathrm{~cm}^3 \end{aligned} $$
$$ \begin{aligned} &\text { Jumlah bilangan guli yang boleh dimasukkan ke dalam bekas }\\ &\begin{aligned} & =4790.76 \mathrm{~cm}^3 \div 0.343 \mathrm{~cm}^3 \\ & =13967.23 \\ & =13967 \text { biji guli } \end{aligned} \end{aligned} $$
Perhatikan rajah di bawah. Diameter hemisfera tersebut ialah 22 cm, hitung
(a) isi padu gabungan bentuk geometri tiga dimensi di bawah.
(b) jumlah bilangan guli dengan isi padu 343 mm3 yang boleh dimasukkan ke dalam bekas tersebut.

Penyelesaian:
(a)
$$ \begin{aligned} \text { Jejari hemisfera } & =22 \mathrm{~cm} \div 2 \\ & =11 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} \text { jejari silinder } & =14 \mathrm{~cm} \div 2 \\ & =7 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} \text { Isi padu gabungan } & =\text { Isi padu hemisfera }+ \text { isi padu silinder } \\ & =\pi j^2 t+\frac{2}{3} \pi j^3 \\ & =\left(\frac{22}{7} \times 7^2 \times 13\right)+\left(\frac{2}{3} \times \frac{22}{7} \times 11^3\right) \\ & =2002+2788.76 \\ & =4790.76 \mathrm{~cm}^3 \end{aligned} $$
(b)
$$ \begin{aligned} \text { Isipadu sebiji guli } & =343 \mathrm{~mm}^3 \\ & =0.343 \mathrm{~cm}^3 \end{aligned} $$
$$ \begin{aligned} &\text { Jumlah bilangan guli yang boleh dimasukkan ke dalam bekas }\\ &\begin{aligned} & =4790.76 \mathrm{~cm}^3 \div 0.343 \mathrm{~cm}^3 \\ & =13967.23 \\ & =13967 \text { biji guli } \end{aligned} \end{aligned} $$