Soalan 1:
Rajah di bawah menunjukkan sebuah bulatan berpusat O. PQR dan STU ialah garis lurus.
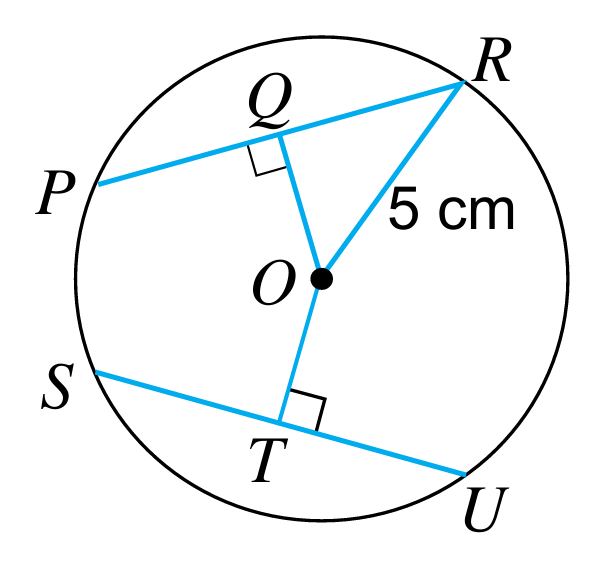
Diberi PQR = STU = 6 cm, hitung panjang yang berikut.
(a) PQ
(b) ST
(c) OT
Penyelesaian:
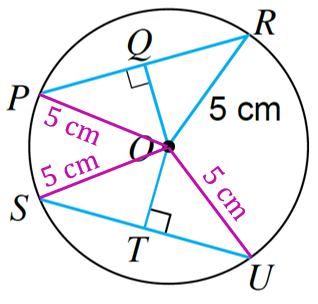
$$ \begin{aligned} &O R=O P=O S=O U=\text { jejari bulatan }=5 \mathrm{~cm}\\ &\therefore \triangle O P R \text { dan } \triangle O S U \text { ialah segi tiga sama kaki } \end{aligned} $$
(a)
$$ \begin{aligned} \text { Diberi } P R & =6 \mathrm{~cm} \\ P Q & =\frac{1}{2} P R \\ & =\frac{1}{2}(6) \\ & =3 \mathrm{~cm} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Diberi } S U=6 \mathrm{~cm}\\ &\begin{aligned} S T & =\frac{1}{2} S U \\ & =\frac{1}{2}(6) \\ & =3 \mathrm{~cm} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Dengan mengguna teorem Pythagores, }\\ &\begin{aligned} O T^2 & =O U^2-T U^2 \\ & =5^2-3^2 \\ & =25-9 \\ & =16 \\ O T & =\sqrt{16} \\ O T & =4 \mathrm{~cm} \end{aligned} \end{aligned} $$
Rajah di bawah menunjukkan sebuah bulatan berpusat O. PQR dan STU ialah garis lurus.

Diberi PQR = STU = 6 cm, hitung panjang yang berikut.
(a) PQ
(b) ST
(c) OT
Penyelesaian:

$$ \begin{aligned} &O R=O P=O S=O U=\text { jejari bulatan }=5 \mathrm{~cm}\\ &\therefore \triangle O P R \text { dan } \triangle O S U \text { ialah segi tiga sama kaki } \end{aligned} $$
(a)
$$ \begin{aligned} \text { Diberi } P R & =6 \mathrm{~cm} \\ P Q & =\frac{1}{2} P R \\ & =\frac{1}{2}(6) \\ & =3 \mathrm{~cm} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Diberi } S U=6 \mathrm{~cm}\\ &\begin{aligned} S T & =\frac{1}{2} S U \\ & =\frac{1}{2}(6) \\ & =3 \mathrm{~cm} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Dengan mengguna teorem Pythagores, }\\ &\begin{aligned} O T^2 & =O U^2-T U^2 \\ & =5^2-3^2 \\ & =25-9 \\ & =16 \\ O T & =\sqrt{16} \\ O T & =4 \mathrm{~cm} \end{aligned} \end{aligned} $$
Soalan 2:
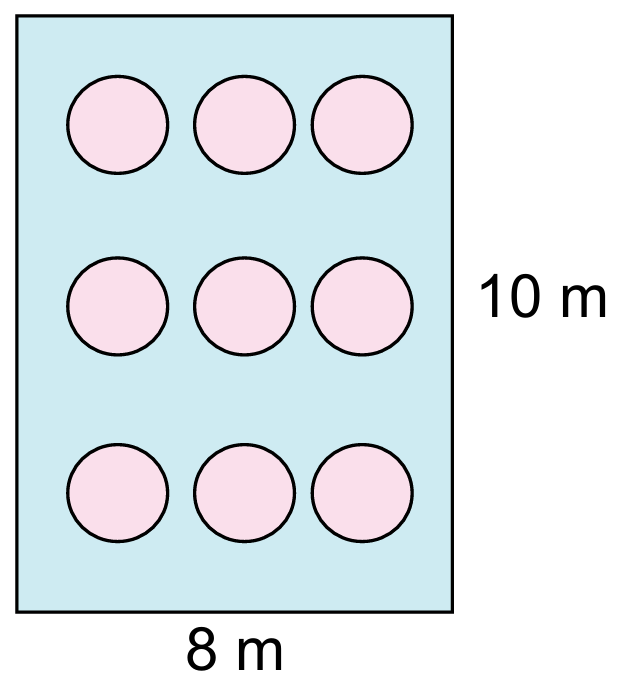
Rajah di sebelah menunjukkan sebuah dewan makan yang berukuran 10 m panjang dan 8 m lebar yang dihamparkan dengan sembilan bidang permaidani berbentuk bulatan. Diameter satu permaidani itu berukuran 200 cm. Hitung luas, dalam meter persegi, kawasan lantai dewan yang tidak diliputi permaidani.
Penyelesaian:
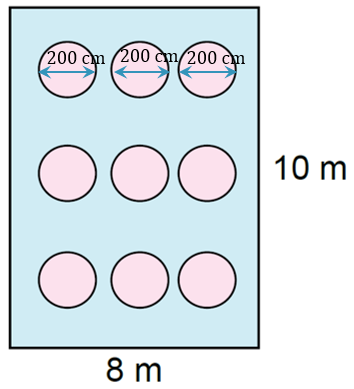
$$ \text { Diberi diameter satu permaidani adalah berukuran } 200 \mathrm{~cm} $$
$$ \begin{aligned} \text { Maka, jejari setiap permaidani bulatan } & =\frac{1}{2}(200 \mathrm{~cm}) \\ & =100 \mathrm{~cm} \\ & =1 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} \text { Luas bagi } 9 \text { keping permaidani bulatan } & =(9)\left(\pi j^2\right) \\ & =(9)\left(\frac{22}{7}\right)(1)^2 \\ & =\frac{198}{7} \mathrm{~m}^2 \end{aligned} $$
$$ \begin{aligned} \text { Luas dewan makan } & =(10)(8) \\ & =80 \mathrm{~m}^2 \end{aligned} $$
$$ \begin{aligned} &\text { Luas kawasan lantai dewan yang tidak diliputi permaidani }\\ &\begin{aligned} & =80-\frac{198}{7} \\ & =\frac{362}{7} \\ & =51.71 \mathrm{~m}^2 \end{aligned} \end{aligned} $$

Rajah di sebelah menunjukkan sebuah dewan makan yang berukuran 10 m panjang dan 8 m lebar yang dihamparkan dengan sembilan bidang permaidani berbentuk bulatan. Diameter satu permaidani itu berukuran 200 cm. Hitung luas, dalam meter persegi, kawasan lantai dewan yang tidak diliputi permaidani.
Penyelesaian:

$$ \text { Diberi diameter satu permaidani adalah berukuran } 200 \mathrm{~cm} $$
$$ \begin{aligned} \text { Maka, jejari setiap permaidani bulatan } & =\frac{1}{2}(200 \mathrm{~cm}) \\ & =100 \mathrm{~cm} \\ & =1 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} \text { Luas bagi } 9 \text { keping permaidani bulatan } & =(9)\left(\pi j^2\right) \\ & =(9)\left(\frac{22}{7}\right)(1)^2 \\ & =\frac{198}{7} \mathrm{~m}^2 \end{aligned} $$
$$ \begin{aligned} \text { Luas dewan makan } & =(10)(8) \\ & =80 \mathrm{~m}^2 \end{aligned} $$
$$ \begin{aligned} &\text { Luas kawasan lantai dewan yang tidak diliputi permaidani }\\ &\begin{aligned} & =80-\frac{198}{7} \\ & =\frac{362}{7} \\ & =51.71 \mathrm{~m}^2 \end{aligned} \end{aligned} $$
Soalan 3:
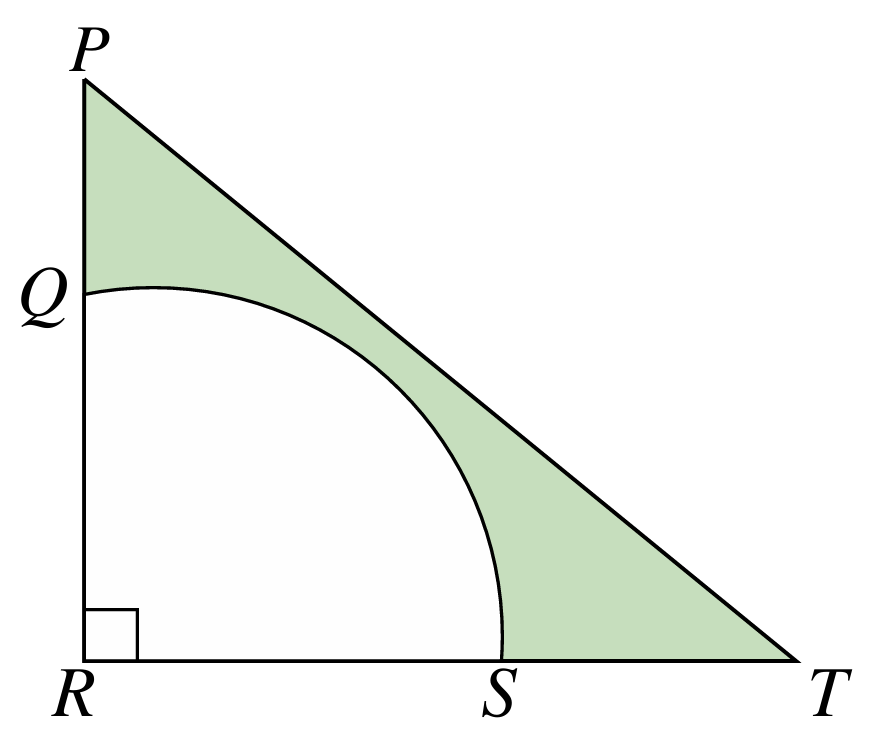
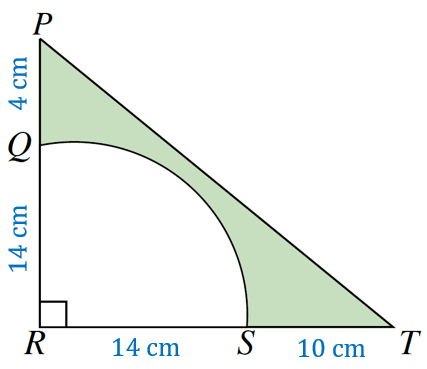
Rajah di sebelah menunjukkan sebuah segi tiga bersudut tegak PRT. R ialah pusat bagi sukuan itu. Diberi RS = 14 cm, ST = 10 cm dan PQ = 4 cm. Hitung perimeter, dalam cm, kawasan berlorek.
(Guna π = 22/7 )
Penyelesaian:
$$ \text { Panjang lengkok }=\frac{\theta}{360^{\circ}} \times 2 \pi j $$
$$ \begin{aligned} &\text { Panjang lengkok QS }\\ &\begin{aligned} & =\frac{90^{\circ}}{360^{\circ}} \times(2)\left(\frac{22}{7}\right) \\ & =22 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \text { Diberi } \triangle P R T \text { ialah segi tiga sudut tegak } $$
$$ \begin{aligned} &\text { Dengan mengguna teorem Pythagores, }\\ &\begin{aligned} P T^2 & =P R^2+R T^2 \\ & =(4+14)^2+(14+10)^2 \\ & =18^2+24^2 \\ & =900 \\ P T & =\sqrt{ } 900 \\ P T & =30 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Perimeter kawasan berlorek } & =P Q+Q S+S T+T P \\ & =4+22+10+30 \\ & =66 \mathrm{~cm} \end{aligned} $$

Rajah di sebelah menunjukkan sebuah segi tiga bersudut tegak PRT. R ialah pusat bagi sukuan itu. Diberi RS = 14 cm, ST = 10 cm dan PQ = 4 cm. Hitung perimeter, dalam cm, kawasan berlorek.
(Guna π = 22/7 )
Penyelesaian:

$$ \text { Panjang lengkok }=\frac{\theta}{360^{\circ}} \times 2 \pi j $$
$$ \begin{aligned} &\text { Panjang lengkok QS }\\ &\begin{aligned} & =\frac{90^{\circ}}{360^{\circ}} \times(2)\left(\frac{22}{7}\right) \\ & =22 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \text { Diberi } \triangle P R T \text { ialah segi tiga sudut tegak } $$
$$ \begin{aligned} &\text { Dengan mengguna teorem Pythagores, }\\ &\begin{aligned} P T^2 & =P R^2+R T^2 \\ & =(4+14)^2+(14+10)^2 \\ & =18^2+24^2 \\ & =900 \\ P T & =\sqrt{ } 900 \\ P T & =30 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Perimeter kawasan berlorek } & =P Q+Q S+S T+T P \\ & =4+22+10+30 \\ & =66 \mathrm{~cm} \end{aligned} $$