Soalan 2:
Hitung nilai p, q, dan r dalam rajah yang berikut.

Penyelesaian:
(a)
$$ \begin{aligned} p+140^{\circ} & =180^{\circ} \\ p & =180^{\circ}-140^{\circ} \\ p & =40^{\circ} \end{aligned} $$
$$ \begin{aligned} q+45^{\circ} & =180^{\circ} \\ q & =180^{\circ}-45^{\circ} \\ q & =135^{\circ} \end{aligned} $$
$$ \begin{aligned} p+r+45^{\circ} & =180^{\circ} \\ 40^{\circ}+r+45^{\circ} & =180^{\circ} \\ r+85^{\circ} & =180^{\circ} \\ r & =180^{\circ}-85^{\circ} \\ r & =95^{\circ} \end{aligned} $$
(b)
$$ \begin{aligned} p+135^{\circ} & =180^{\circ} \\ p & =180^{\circ}-135^{\circ} \\ p & =45^{\circ} \end{aligned} $$
$$ \begin{aligned} q+85^{\circ} & =180^{\circ} \\ q & =180^{\circ}-85^{\circ} \\ q & =95^{\circ} \end{aligned} $$
$$ \begin{aligned} &\text { Hasil tambah sudut peluaran }=360^{\circ}\\ &\begin{aligned} r+90^{\circ}+85^{\circ}+135^{\circ} & =360^{\circ} \\ r+310^{\circ} & =360^{\circ} \\ r & =360^{\circ}-310^{\circ} \\ r & =50^{\circ} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} p+105^{\circ} & =180^{\circ} \\ p & =180^{\circ}-105^{\circ} \\ p & =75^{\circ} \end{aligned} $$
$$ \begin{aligned} q+40^{\circ} & =180^{\circ} \\ q & =180^{\circ}-40^{\circ} \\ q & =40^{\circ} \end{aligned} $$
$$ \begin{aligned} r+75^{\circ} & =180^{\circ} \\ r & =180^{\circ}-75^{\circ} \\ r & =105^{\circ} \end{aligned} $$
Hitung nilai p, q, dan r dalam rajah yang berikut.

Penyelesaian:
(a)
$$ \begin{aligned} p+140^{\circ} & =180^{\circ} \\ p & =180^{\circ}-140^{\circ} \\ p & =40^{\circ} \end{aligned} $$
$$ \begin{aligned} q+45^{\circ} & =180^{\circ} \\ q & =180^{\circ}-45^{\circ} \\ q & =135^{\circ} \end{aligned} $$
$$ \begin{aligned} p+r+45^{\circ} & =180^{\circ} \\ 40^{\circ}+r+45^{\circ} & =180^{\circ} \\ r+85^{\circ} & =180^{\circ} \\ r & =180^{\circ}-85^{\circ} \\ r & =95^{\circ} \end{aligned} $$
(b)
$$ \begin{aligned} p+135^{\circ} & =180^{\circ} \\ p & =180^{\circ}-135^{\circ} \\ p & =45^{\circ} \end{aligned} $$
$$ \begin{aligned} q+85^{\circ} & =180^{\circ} \\ q & =180^{\circ}-85^{\circ} \\ q & =95^{\circ} \end{aligned} $$
$$ \begin{aligned} &\text { Hasil tambah sudut peluaran }=360^{\circ}\\ &\begin{aligned} r+90^{\circ}+85^{\circ}+135^{\circ} & =360^{\circ} \\ r+310^{\circ} & =360^{\circ} \\ r & =360^{\circ}-310^{\circ} \\ r & =50^{\circ} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} p+105^{\circ} & =180^{\circ} \\ p & =180^{\circ}-105^{\circ} \\ p & =75^{\circ} \end{aligned} $$
$$ \begin{aligned} q+40^{\circ} & =180^{\circ} \\ q & =180^{\circ}-40^{\circ} \\ q & =40^{\circ} \end{aligned} $$
$$ \begin{aligned} r+75^{\circ} & =180^{\circ} \\ r & =180^{\circ}-75^{\circ} \\ r & =105^{\circ} \end{aligned} $$
Soalan 3:
Hitung nilai x bagi poligon berikut.

Penyelesaian:
(a)
$$ \begin{aligned} x+2 x+90^{\circ}+120^{\circ} & =360^{\circ} \\ 3 x+210^{\circ} & =360^{\circ} \\ 3 x & =360^{\circ}-210^{\circ} \\ 3 x & =150^{\circ} \\ x & =50^{\circ} \end{aligned} $$
(b)
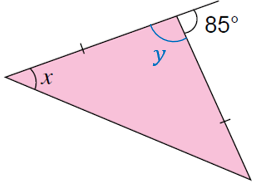
$$ \begin{aligned} y+85^{\circ} & =180^{\circ} \\ y & =180^{\circ}-85^{\circ} \\ y & =95^{\circ} \end{aligned} $$
$$ \begin{aligned} &\text { Segi tiga sama kaki, }\\ &\begin{aligned} x+x+95^{\circ} & =180^{\circ} \\ 2 x & =180^{\circ}-95^{\circ} \\ 2 x & =85^{\circ} \\ x & =42.5^{\circ} \end{aligned} \end{aligned} $$
(c)
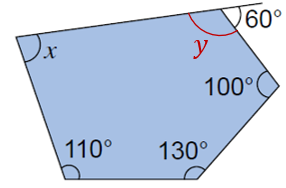
$$ \begin{aligned} y+60^{\circ} & =180^{\circ} \\ y & =180^{\circ}-60^{\circ} \\ y & =120^{\circ} \end{aligned} $$
$$ \begin{aligned} &\text { Hasil tambah sudut pedalaman suatu poligon }=(n-2) \times 180^{\circ}\\ &\begin{aligned} x+y+100^{\circ}+130^{\circ}+110^{\circ} & =(5-2) \times 180^{\circ} \\ x+120^{\circ}+100^{\circ}+130^{\circ}+110^{\circ} & =3 \times 180^{\circ} \\ x+460^{\circ} & =540^{\circ} \\ x & =540^{\circ}-460^{\circ} \\ x & =80^{\circ} \end{aligned} \end{aligned} $$
Hitung nilai x bagi poligon berikut.

Penyelesaian:
(a)
$$ \begin{aligned} x+2 x+90^{\circ}+120^{\circ} & =360^{\circ} \\ 3 x+210^{\circ} & =360^{\circ} \\ 3 x & =360^{\circ}-210^{\circ} \\ 3 x & =150^{\circ} \\ x & =50^{\circ} \end{aligned} $$
(b)

$$ \begin{aligned} y+85^{\circ} & =180^{\circ} \\ y & =180^{\circ}-85^{\circ} \\ y & =95^{\circ} \end{aligned} $$
$$ \begin{aligned} &\text { Segi tiga sama kaki, }\\ &\begin{aligned} x+x+95^{\circ} & =180^{\circ} \\ 2 x & =180^{\circ}-95^{\circ} \\ 2 x & =85^{\circ} \\ x & =42.5^{\circ} \end{aligned} \end{aligned} $$
(c)

$$ \begin{aligned} y+60^{\circ} & =180^{\circ} \\ y & =180^{\circ}-60^{\circ} \\ y & =120^{\circ} \end{aligned} $$
$$ \begin{aligned} &\text { Hasil tambah sudut pedalaman suatu poligon }=(n-2) \times 180^{\circ}\\ &\begin{aligned} x+y+100^{\circ}+130^{\circ}+110^{\circ} & =(5-2) \times 180^{\circ} \\ x+120^{\circ}+100^{\circ}+130^{\circ}+110^{\circ} & =3 \times 180^{\circ} \\ x+460^{\circ} & =540^{\circ} \\ x & =540^{\circ}-460^{\circ} \\ x & =80^{\circ} \end{aligned} \end{aligned} $$
Soalan 4:
Hitung bilangan sisi bagi setiap poligon sekata berikut.
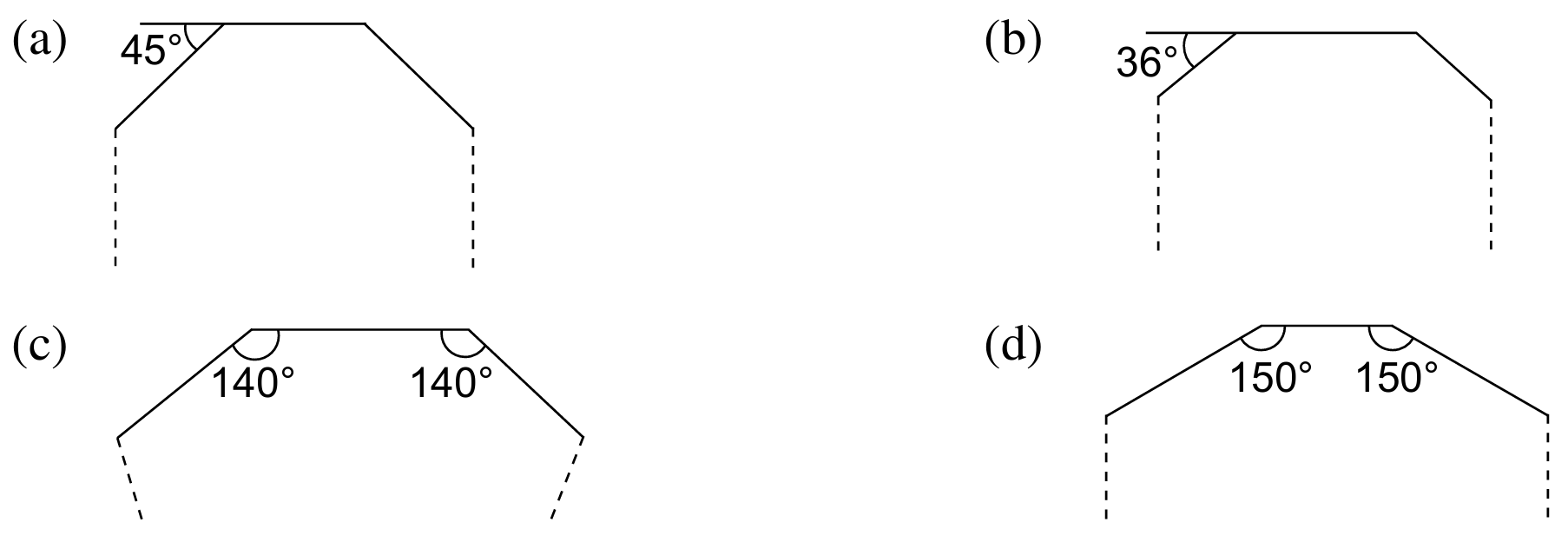
Penyelesaian:
(a)
$$ \begin{aligned} & \text { Bilangan sisi, } n=\frac{360^{\circ}}{\text { sudut peluaran }} \\ & =\frac{360^{\circ}}{45^{\circ}} \\ & =8 \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Bilangan sisi, } n\\ &\begin{aligned} & =\frac{360^{\circ}}{36^{\circ}} \\ & =10 \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Bilangan sisi, } n\\ &\begin{aligned} & =\frac{360^{\circ}}{180^{\circ}-140^{\circ}} \\ & =9 \end{aligned} \end{aligned} $$
(d)
$$ \begin{aligned} &\text { Bilangan sisi, } n\\ &\begin{aligned} & =\frac{360^{\circ}}{180^{\circ}-150^{\circ}} \\ & =12 \end{aligned} \end{aligned} $$
Hitung bilangan sisi bagi setiap poligon sekata berikut.

Penyelesaian:
(a)
$$ \begin{aligned} & \text { Bilangan sisi, } n=\frac{360^{\circ}}{\text { sudut peluaran }} \\ & =\frac{360^{\circ}}{45^{\circ}} \\ & =8 \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Bilangan sisi, } n\\ &\begin{aligned} & =\frac{360^{\circ}}{36^{\circ}} \\ & =10 \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Bilangan sisi, } n\\ &\begin{aligned} & =\frac{360^{\circ}}{180^{\circ}-140^{\circ}} \\ & =9 \end{aligned} \end{aligned} $$
(d)
$$ \begin{aligned} &\text { Bilangan sisi, } n\\ &\begin{aligned} & =\frac{360^{\circ}}{180^{\circ}-150^{\circ}} \\ & =12 \end{aligned} \end{aligned} $$