Soalan 4:
Bagi setiap rajah di bawah, hitung nilai p, q dan r.
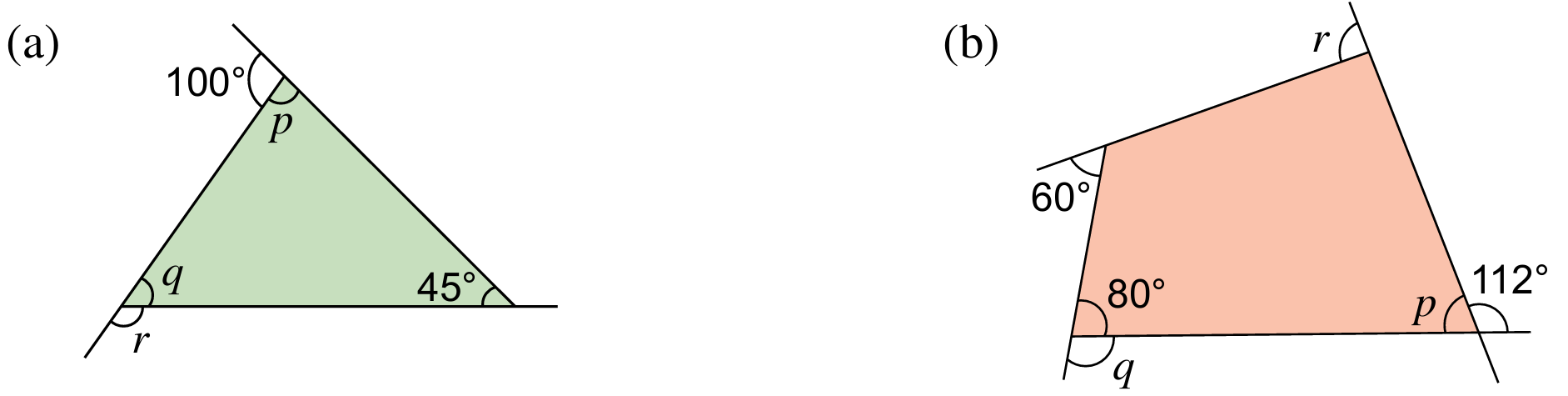
Penyelesaian:
(a)
$$ \begin{aligned} p+100^{\circ} & =180^{\circ} \\ p & =180^{\circ}-100^{\circ} \\ p & =80^{\circ} \end{aligned} $$
$$ \begin{aligned} p+q+45^{\circ} & =180^{\circ} \\ 80^{\circ}+q+45^{\circ} & =180^{\circ} \\ q+125^{\circ} & =180^{\circ} \\ q & =180^{\circ}-125^{\circ} \\ q & =55^{\circ} \end{aligned} $$
$$ \begin{aligned} q+r & =180^{\circ} \\ 55^{\circ}+r & =180^{\circ} \\ r & =180^{\circ}-55^{\circ} \\ r & =125^{\circ} \end{aligned} $$
(b)
$$ \begin{aligned} p+112^{\circ} & =180^{\circ} \\ p & =180^{\circ}-112^{\circ} \\ p & =68^{\circ} \end{aligned} $$
$$ \begin{aligned} q+80^{\circ} & =180^{\circ} \\ q & =180^{\circ}-80^{\circ} \\ q & =100^{\circ} \end{aligned} $$
$$ \begin{aligned} &\text { Hasil tambah sudut peluaran }=360^{\circ}\\ &\begin{aligned} r+112^{\circ}+q+60^{\circ} & =360^{\circ} \\ r+112^{\circ}+100^{\circ}+60^{\circ} & =360^{\circ} \\ r+272^{\circ} & =360^{\circ} \\ r & =88^{\circ} \end{aligned} \end{aligned} $$
Bagi setiap rajah di bawah, hitung nilai p, q dan r.
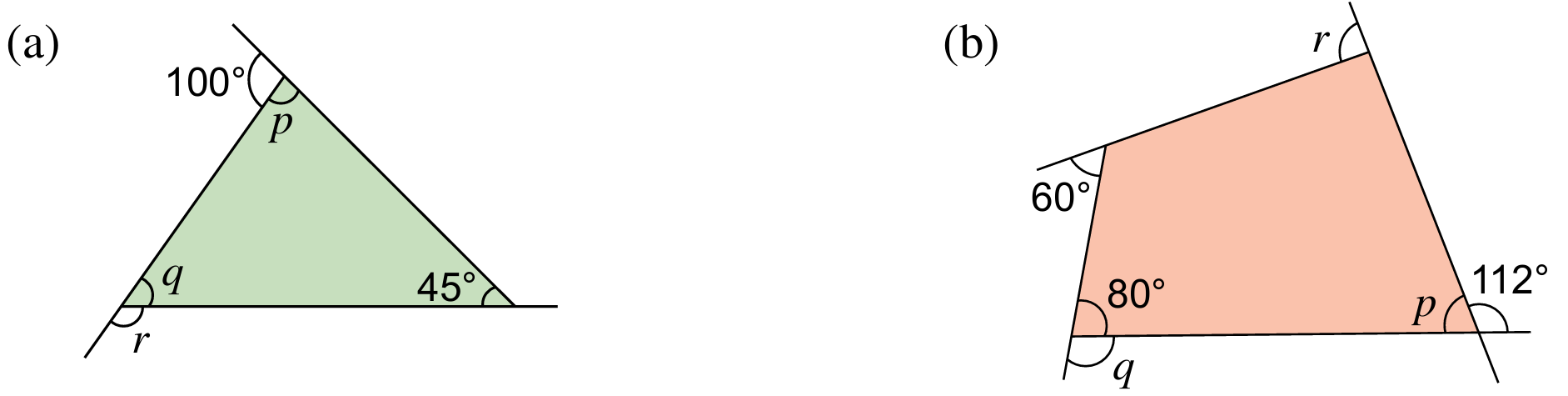
Penyelesaian:
(a)
$$ \begin{aligned} p+100^{\circ} & =180^{\circ} \\ p & =180^{\circ}-100^{\circ} \\ p & =80^{\circ} \end{aligned} $$
$$ \begin{aligned} p+q+45^{\circ} & =180^{\circ} \\ 80^{\circ}+q+45^{\circ} & =180^{\circ} \\ q+125^{\circ} & =180^{\circ} \\ q & =180^{\circ}-125^{\circ} \\ q & =55^{\circ} \end{aligned} $$
$$ \begin{aligned} q+r & =180^{\circ} \\ 55^{\circ}+r & =180^{\circ} \\ r & =180^{\circ}-55^{\circ} \\ r & =125^{\circ} \end{aligned} $$
(b)
$$ \begin{aligned} p+112^{\circ} & =180^{\circ} \\ p & =180^{\circ}-112^{\circ} \\ p & =68^{\circ} \end{aligned} $$
$$ \begin{aligned} q+80^{\circ} & =180^{\circ} \\ q & =180^{\circ}-80^{\circ} \\ q & =100^{\circ} \end{aligned} $$
$$ \begin{aligned} &\text { Hasil tambah sudut peluaran }=360^{\circ}\\ &\begin{aligned} r+112^{\circ}+q+60^{\circ} & =360^{\circ} \\ r+112^{\circ}+100^{\circ}+60^{\circ} & =360^{\circ} \\ r+272^{\circ} & =360^{\circ} \\ r & =88^{\circ} \end{aligned} \end{aligned} $$
Soalan 5:
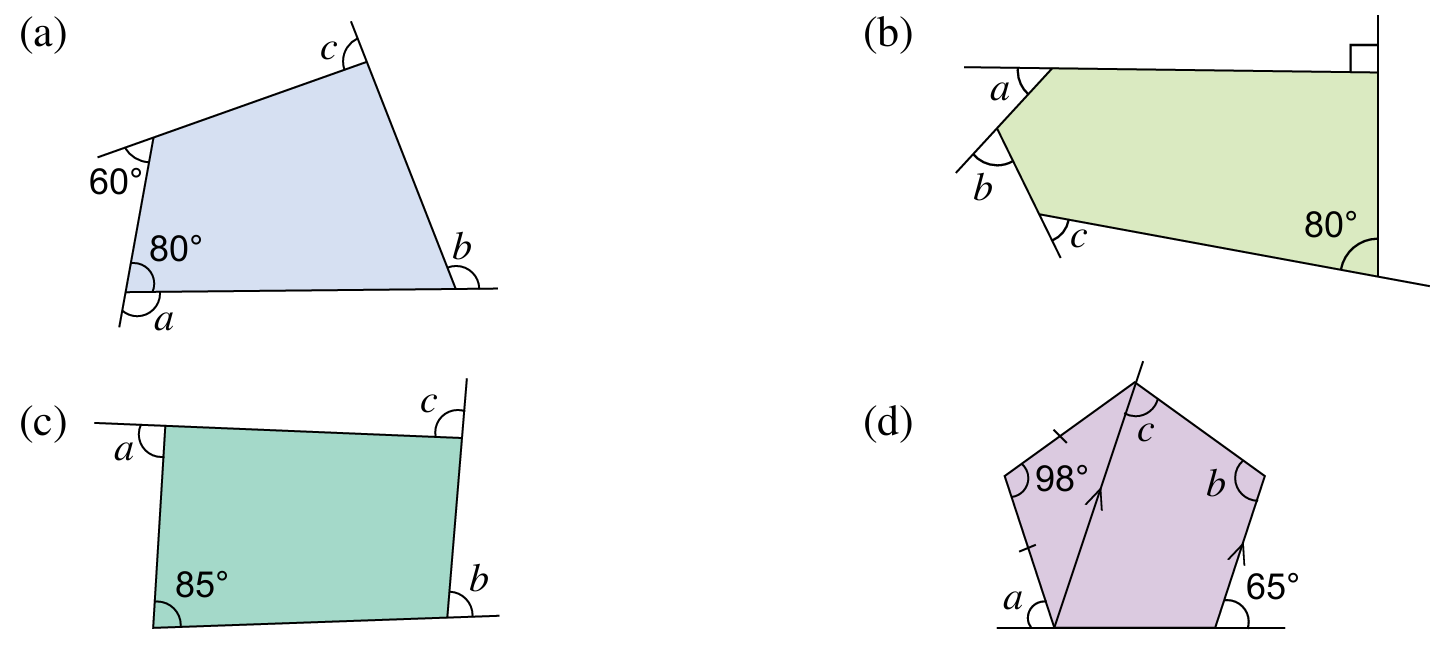
Hitung nilai a + b + c.
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Hasil tambah sudut peluaran }=360^{\circ}\\ &\begin{aligned} & a+b+c+60^{\circ}=360^{\circ} \\ & a+b+c=360^{\circ}-60^{\circ} \\ & a+b+c=300^{\circ} \end{aligned} \end{aligned} $$
(b)
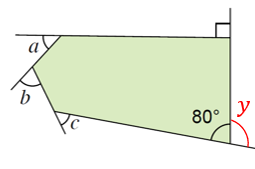
$$ \begin{aligned} &\begin{aligned} y+80^{\circ} & =180^{\circ} \\ y & =100^{\circ} \end{aligned}\\ &\text { Hasil tambah sudut peluaran }=360^{\circ}\\ &\begin{aligned} a+b+c+100^{\circ}+90^{\circ} & =360^{\circ} \\ a+b+c & =360^{\circ}-190^{\circ} \\ a+b+c & =170^{\circ} \end{aligned} \end{aligned} $$
(c)
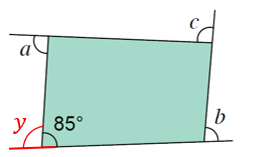
$$ \begin{aligned} &\begin{aligned} y+85^{\circ} & =180^{\circ} \\ y & =95^{\circ} \end{aligned}\\ &\text { Hasil tambah sudut peluaran }=360^{\circ}\\ &\begin{aligned} & a+b+c+95^{\circ}=360^{\circ} \\ & a+b+c=360^{\circ}-95^{\circ} \\ & a+b+c=265^{\circ} \end{aligned} \end{aligned} $$
(d)
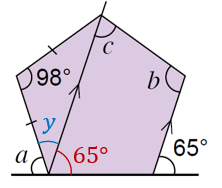
$$ \begin{aligned} y & =\left(180^{\circ}-98^{\circ}\right) \div 2 \\ & =82^{\circ} \div 2 \\ & =41^{\circ} \end{aligned} $$
$$ \begin{array}{r} a+y+65^{\circ}=180^{\circ} \\ a+41^{\circ}+65^{\circ}=180^{\circ} \\ a+106^{\circ}=180^{\circ} \\ a=74^{\circ} \end{array} $$
$$ \begin{aligned} b+c & =180^{\circ} \\ b+c+a & =180^{\circ}+74^{\circ} \\ a+b+c & =254^{\circ} \end{aligned} $$
Hitung nilai a + b + c.

Penyelesaian:
(a)
$$ \begin{aligned} &\text { Hasil tambah sudut peluaran }=360^{\circ}\\ &\begin{aligned} & a+b+c+60^{\circ}=360^{\circ} \\ & a+b+c=360^{\circ}-60^{\circ} \\ & a+b+c=300^{\circ} \end{aligned} \end{aligned} $$
(b)

$$ \begin{aligned} &\begin{aligned} y+80^{\circ} & =180^{\circ} \\ y & =100^{\circ} \end{aligned}\\ &\text { Hasil tambah sudut peluaran }=360^{\circ}\\ &\begin{aligned} a+b+c+100^{\circ}+90^{\circ} & =360^{\circ} \\ a+b+c & =360^{\circ}-190^{\circ} \\ a+b+c & =170^{\circ} \end{aligned} \end{aligned} $$
(c)

$$ \begin{aligned} &\begin{aligned} y+85^{\circ} & =180^{\circ} \\ y & =95^{\circ} \end{aligned}\\ &\text { Hasil tambah sudut peluaran }=360^{\circ}\\ &\begin{aligned} & a+b+c+95^{\circ}=360^{\circ} \\ & a+b+c=360^{\circ}-95^{\circ} \\ & a+b+c=265^{\circ} \end{aligned} \end{aligned} $$
(d)

$$ \begin{aligned} y & =\left(180^{\circ}-98^{\circ}\right) \div 2 \\ & =82^{\circ} \div 2 \\ & =41^{\circ} \end{aligned} $$
$$ \begin{array}{r} a+y+65^{\circ}=180^{\circ} \\ a+41^{\circ}+65^{\circ}=180^{\circ} \\ a+106^{\circ}=180^{\circ} \\ a=74^{\circ} \end{array} $$
$$ \begin{aligned} b+c & =180^{\circ} \\ b+c+a & =180^{\circ}+74^{\circ} \\ a+b+c & =254^{\circ} \end{aligned} $$