Soalan 8:
Swee Lee sepatutnya dapat menyiapkan (28 + 16x) bilangan soalan matematik dalam masa 4 jam.
(i) Berapakah bilangan soalan yang dapat disiapkan dalam masa 30 minit?
(ii) Sekiranya Swee Lee hanya dapat menyiapkan (14 + 8x) bilangan soalan tersebut, berapa lamakah masa yang diambilnya?
Penyelesaian:
$$ 4 \text { jam }=4 \times 60=240 \text { minit } $$
(i)
$$ \begin{aligned} &\text { Bilangan soalan yang dapat disiapkan dalam masa } 30 \text { minit }\\ &\begin{aligned} & =(28+16 x) \times \frac{30}{240} \\ & =(28+16 x) \times \frac{1}{8} \\ & =\frac{28}{8}+\frac{16 x}{8} \\ & =\frac{28+16 x}{8} \\ & =\frac{4(7+4 x)}{8} \\ & =\frac{7+4 x}{2} \end{aligned} \end{aligned} $$
(ii)
$$ \begin{aligned} &\text { Masa yang diambil untuk menyiapkan }(14+8 x) \text { soalan }\\ &\begin{aligned} & =\frac{4 \text { jam }}{(28+16 x) \text { soalan }} \times(14+8 x) \text { soalan } \\ & =\frac{4 \text { jam }}{2(14+8 x) \text { soalan }} \times(14+8 x) \text { soalan } \\ & =\frac{4 \mathrm{jam}}{2} \\ & =2 \mathrm{jam} \end{aligned} \end{aligned} $$
Swee Lee sepatutnya dapat menyiapkan (28 + 16x) bilangan soalan matematik dalam masa 4 jam.
(i) Berapakah bilangan soalan yang dapat disiapkan dalam masa 30 minit?
(ii) Sekiranya Swee Lee hanya dapat menyiapkan (14 + 8x) bilangan soalan tersebut, berapa lamakah masa yang diambilnya?
Penyelesaian:
$$ 4 \text { jam }=4 \times 60=240 \text { minit } $$
(i)
$$ \begin{aligned} &\text { Bilangan soalan yang dapat disiapkan dalam masa } 30 \text { minit }\\ &\begin{aligned} & =(28+16 x) \times \frac{30}{240} \\ & =(28+16 x) \times \frac{1}{8} \\ & =\frac{28}{8}+\frac{16 x}{8} \\ & =\frac{28+16 x}{8} \\ & =\frac{4(7+4 x)}{8} \\ & =\frac{7+4 x}{2} \end{aligned} \end{aligned} $$
(ii)
$$ \begin{aligned} &\text { Masa yang diambil untuk menyiapkan }(14+8 x) \text { soalan }\\ &\begin{aligned} & =\frac{4 \text { jam }}{(28+16 x) \text { soalan }} \times(14+8 x) \text { soalan } \\ & =\frac{4 \text { jam }}{2(14+8 x) \text { soalan }} \times(14+8 x) \text { soalan } \\ & =\frac{4 \mathrm{jam}}{2} \\ & =2 \mathrm{jam} \end{aligned} \end{aligned} $$
Soalan 9:
Azimah membuat seloyang kuih lapis berbentuk segi empat tepat berukuran (3x + 2) cm panjang dan (x + 2) cm lebar. Dia memotong kuih lapis tersebut kepada 6 bahagian panjang dan 3 bahagian lebar. Hitung luas sepotong kuih lapis tersebut dalam bentuk ungkapan algebra.
Penyelesaian:
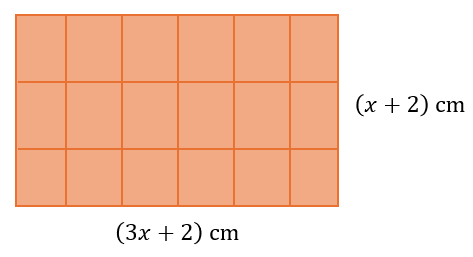
$$ \begin{aligned} \text { Luas sepotong kuih lapis } & =\left(\frac{3 x+2}{6}\right)\left(\frac{x+2}{3}\right) \\ & =\frac{(3 x+2)(x+2)}{18} \\ & =\frac{3 x^2+6 x+2 x+4}{18} \\ & =\left(\frac{3 x^2+8 x+4}{18}\right) \mathrm{cm}^2 \end{aligned} $$
Azimah membuat seloyang kuih lapis berbentuk segi empat tepat berukuran (3x + 2) cm panjang dan (x + 2) cm lebar. Dia memotong kuih lapis tersebut kepada 6 bahagian panjang dan 3 bahagian lebar. Hitung luas sepotong kuih lapis tersebut dalam bentuk ungkapan algebra.
Penyelesaian:

$$ \begin{aligned} \text { Luas sepotong kuih lapis } & =\left(\frac{3 x+2}{6}\right)\left(\frac{x+2}{3}\right) \\ & =\frac{(3 x+2)(x+2)}{18} \\ & =\frac{3 x^2+6 x+2 x+4}{18} \\ & =\left(\frac{3 x^2+8 x+4}{18}\right) \mathrm{cm}^2 \end{aligned} $$
Soalan 10:
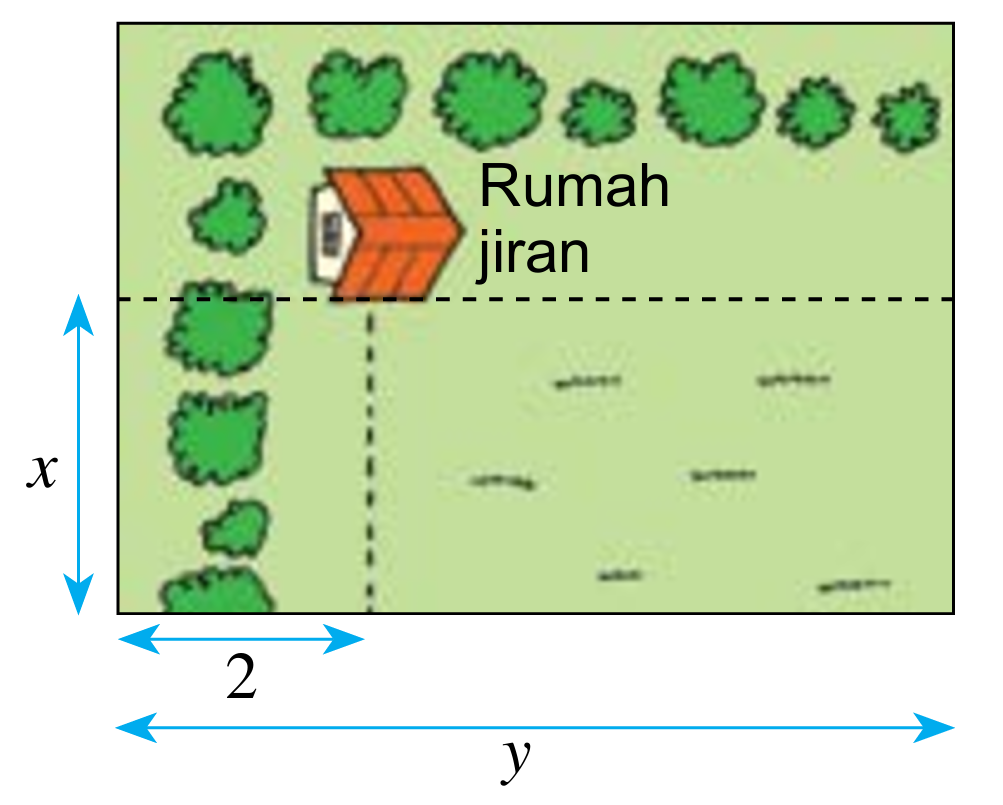
Encik Hanapi ingin mendirikan sebuah banglo satu tingkat di sebidang tanah berukuran x meter lebar dan y meter panjang. Dia perlu menyediakan 2 meter rizab jalan untuk jirannya.
(i) Berapakah luas tanah Encik Hanapi yang asal?
(ii) Berapakah perbezaan luas tanah yang asal dengan luas tanah selepas ditolak rizab jalan?
(iii) Sekiranya harga tanah ialah RM18 per meter persegi, berapakah harga keseluruhan tanah Encik Hanapi?
Penyelesaian:
(i)
$$ \begin{aligned} \text { Luas tanah Encik Hanapi yang asal } & =(x)(y) \\ & =x y \mathrm{~m}^2 \end{aligned} $$
(ii)
$$ \begin{aligned} \text { Perbezaan luas tanah } & =x y-(2)(x) \\ & =(x y-2 x) m^2 \end{aligned} $$
(iii)
$$ \begin{aligned} \text { Harga keseluruhan tanah Encik Hanapi } & =(x y)(18) \\ & =18 x y \\ & =\mathrm{RM}(18 x y) \end{aligned} $$

Encik Hanapi ingin mendirikan sebuah banglo satu tingkat di sebidang tanah berukuran x meter lebar dan y meter panjang. Dia perlu menyediakan 2 meter rizab jalan untuk jirannya.
(i) Berapakah luas tanah Encik Hanapi yang asal?
(ii) Berapakah perbezaan luas tanah yang asal dengan luas tanah selepas ditolak rizab jalan?
(iii) Sekiranya harga tanah ialah RM18 per meter persegi, berapakah harga keseluruhan tanah Encik Hanapi?
Penyelesaian:
(i)
$$ \begin{aligned} \text { Luas tanah Encik Hanapi yang asal } & =(x)(y) \\ & =x y \mathrm{~m}^2 \end{aligned} $$
(ii)
$$ \begin{aligned} \text { Perbezaan luas tanah } & =x y-(2)(x) \\ & =(x y-2 x) m^2 \end{aligned} $$
(iii)
$$ \begin{aligned} \text { Harga keseluruhan tanah Encik Hanapi } & =(x y)(18) \\ & =18 x y \\ & =\mathrm{RM}(18 x y) \end{aligned} $$