Soalan 6:
Mohan telah menggunakan setin cat untuk mengecat seluruh kawasan latar pentas yang berbentuk segi empat sama. Setin cat dapat meliputi 38 m2 seluruh kawasan latar pentas. Anggarkan panjang sisi latar pentas itu.
Penyelesaian:
38 adalah antara kuasa dua sempurna 36 dengan 49.
√38 adalah antara √36 dengan √49.
iaitu, √38 adalah antara 6 dengan 7.
Maka, √38 ≈ 6.
Anggaran panjang sisi latar pentas adalah 6 m.
Mohan telah menggunakan setin cat untuk mengecat seluruh kawasan latar pentas yang berbentuk segi empat sama. Setin cat dapat meliputi 38 m2 seluruh kawasan latar pentas. Anggarkan panjang sisi latar pentas itu.
Penyelesaian:
38 adalah antara kuasa dua sempurna 36 dengan 49.
√38 adalah antara √36 dengan √49.
iaitu, √38 adalah antara 6 dengan 7.
Maka, √38 ≈ 6.
Anggaran panjang sisi latar pentas adalah 6 m.
Soalan 7:
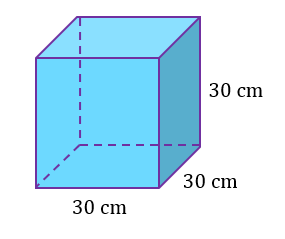
Sebuah kubus besar dengan panjang tepi 30 cm dipotong kepada 27 buah kubus kecil yang sama saiz. Cari
(a) panjang tepi setiap kubus kecil itu,
(b) luas muka atas setiap kubus kecil itu.
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Isipadu kucus besar }\\ &\begin{aligned} & =30 \mathrm{~cm} \times 30 \mathrm{~cm} \times 30 \mathrm{~cm} \\ & =27000 \mathrm{~cm}^3 \end{aligned} \end{aligned} $$
Kubus besar kemudian dipotong kpd 27 buah kubus kecil yg sama saiz
$$ \begin{aligned} &\text { Maka, isipadu setiap kubus kecil }\\ &\begin{aligned} & =27000 \mathrm{~cm}^3 \div 27 \\ & =1000 \mathrm{~cm}^3 \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Panjang tepi setiap kubus kecil } & =\sqrt[3]{1000} \\ & =10 \mathrm{~cm} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Luas muka atas setiap kubus kecil }\\ &\begin{aligned} & =10 \mathrm{~cm} \times 10 \mathrm{~cm} \\ & =100 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
Sebuah kubus besar dengan panjang tepi 30 cm dipotong kepada 27 buah kubus kecil yang sama saiz. Cari
(a) panjang tepi setiap kubus kecil itu,
(b) luas muka atas setiap kubus kecil itu.
Penyelesaian:

(a)
$$ \begin{aligned} &\text { Isipadu kucus besar }\\ &\begin{aligned} & =30 \mathrm{~cm} \times 30 \mathrm{~cm} \times 30 \mathrm{~cm} \\ & =27000 \mathrm{~cm}^3 \end{aligned} \end{aligned} $$
Kubus besar kemudian dipotong kpd 27 buah kubus kecil yg sama saiz
$$ \begin{aligned} &\text { Maka, isipadu setiap kubus kecil }\\ &\begin{aligned} & =27000 \mathrm{~cm}^3 \div 27 \\ & =1000 \mathrm{~cm}^3 \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Panjang tepi setiap kubus kecil } & =\sqrt[3]{1000} \\ & =10 \mathrm{~cm} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Luas muka atas setiap kubus kecil }\\ &\begin{aligned} & =10 \mathrm{~cm} \times 10 \mathrm{~cm} \\ & =100 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
Soalan 8:
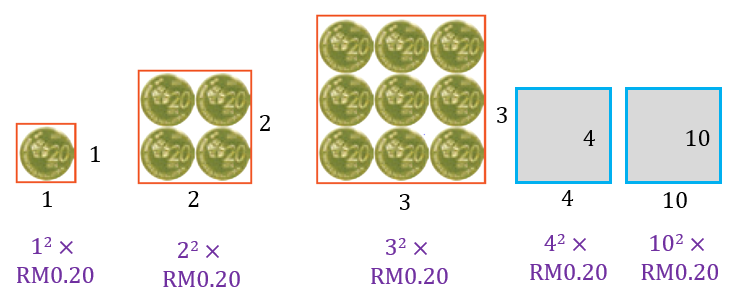
Amirul menyusun duit syiling 20 sen kepada segi empat sama seperti yang ditunjukkan dalam rajah di bawah.

(a) Hitung jumlah nilai, dalam RM, bagi segi empat sama yang
(i) keempat,
(ii) ke-10.
(b) Jika Amirul mempunyai duit syiling 20 sen yang bernilai sejumlah RM60, tentukan susunan duit syiling 20 sen untuk membentuk segi empat sama terbesar.
Penyelesaian:
(a)(i)
$$ \begin{aligned} &\text { Nilai, dalam RM, bagi segi empat sama yang keempat }\\ &\begin{aligned} & =4^2 \times \mathrm{RM} 0.20 \\ & =\mathrm{RM} 3.20 \end{aligned} \end{aligned} $$
(a)(ii)
$$ \begin{aligned} &\text { Nilai, dalam RM, bagi segi empat sama yang ke-10 }\\ &\begin{aligned} & =10^2 \times \mathrm{RM} 0.20 \\ & =\mathrm{RM} 20.00 \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Jumlah kepingan } 20 \text { sen dalam RM60 }\\ &\begin{aligned} & =\mathrm{RM} 60 \div \text { RM } 0.20 \\ & =300 \text { keping duit syiling } \end{aligned} \end{aligned} $$
300 adalah antara 289 dengan 324.
√300 adalah antara √289 dengan √324.
iaitu, √300 adalah antara 17 dengan 18.
Jadi, ukuran bagi segi empat terbesar yang dapat disusun ialah 17 × 17.
Amirul menyusun duit syiling 20 sen kepada segi empat sama seperti yang ditunjukkan dalam rajah di bawah.

(a) Hitung jumlah nilai, dalam RM, bagi segi empat sama yang
(i) keempat,
(ii) ke-10.
(b) Jika Amirul mempunyai duit syiling 20 sen yang bernilai sejumlah RM60, tentukan susunan duit syiling 20 sen untuk membentuk segi empat sama terbesar.
Penyelesaian:

(a)(i)
$$ \begin{aligned} &\text { Nilai, dalam RM, bagi segi empat sama yang keempat }\\ &\begin{aligned} & =4^2 \times \mathrm{RM} 0.20 \\ & =\mathrm{RM} 3.20 \end{aligned} \end{aligned} $$
(a)(ii)
$$ \begin{aligned} &\text { Nilai, dalam RM, bagi segi empat sama yang ke-10 }\\ &\begin{aligned} & =10^2 \times \mathrm{RM} 0.20 \\ & =\mathrm{RM} 20.00 \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Jumlah kepingan } 20 \text { sen dalam RM60 }\\ &\begin{aligned} & =\mathrm{RM} 60 \div \text { RM } 0.20 \\ & =300 \text { keping duit syiling } \end{aligned} \end{aligned} $$
300 adalah antara 289 dengan 324.
√300 adalah antara √289 dengan √324.
iaitu, √300 adalah antara 17 dengan 18.
Jadi, ukuran bagi segi empat terbesar yang dapat disusun ialah 17 × 17.
Soalan 9:
Stella ingin menyerikan patio rumahnya dengan memasang kepingan batu pemijak yang berbentuk segi empat sama. Setiap kepingan batu pemijak mempunyai luas 1 m2. Dia membuat lakaran pelan pemasangan seperti yang ditunjukkan dalam rajah di sebelah.
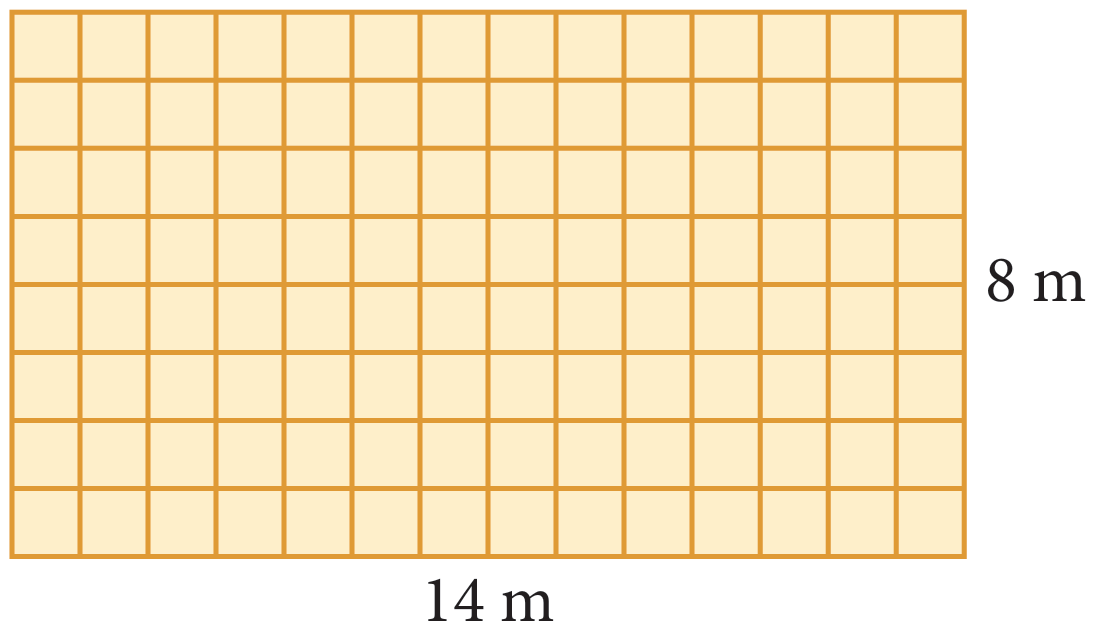
(a) Berapakah jumlah kepingan batu pemijak yang digunakan dalam pembinaannya?
(b) Jika Stella bercadang menggunakan bilangan kepingan batu pemijak yang sama seperti (a) tetapi mengubah pelan pemasangan kepada bentuk segi empat sama, adakah ini dapat dilakukan oleh Stella? Terangkan jawapan anda.
Penyelesaian:
(a)
$$ \begin{aligned} \text { Luas patio rumah } & =14 \times 8 \\ & =112 \mathrm{~m}^2 \end{aligned} $$
Diberi setiap kepingan batu pemijak mempunyai luas 1 m2
$$ \begin{aligned} &\text { Jumlah kepingan batu pemijak yang digunakan dalam pembinaan }\\ &\begin{aligned} & =112 \mathrm{~m}^2 \div 1 \mathrm{~m}^2 \\ & =112 \mathrm{keping} \end{aligned} \end{aligned} $$
(b)
Tidak boleh
112 bukan kuasa dua sempurna.
Stella ingin menyerikan patio rumahnya dengan memasang kepingan batu pemijak yang berbentuk segi empat sama. Setiap kepingan batu pemijak mempunyai luas 1 m2. Dia membuat lakaran pelan pemasangan seperti yang ditunjukkan dalam rajah di sebelah.

(a) Berapakah jumlah kepingan batu pemijak yang digunakan dalam pembinaannya?
(b) Jika Stella bercadang menggunakan bilangan kepingan batu pemijak yang sama seperti (a) tetapi mengubah pelan pemasangan kepada bentuk segi empat sama, adakah ini dapat dilakukan oleh Stella? Terangkan jawapan anda.
Penyelesaian:
(a)
$$ \begin{aligned} \text { Luas patio rumah } & =14 \times 8 \\ & =112 \mathrm{~m}^2 \end{aligned} $$
Diberi setiap kepingan batu pemijak mempunyai luas 1 m2
$$ \begin{aligned} &\text { Jumlah kepingan batu pemijak yang digunakan dalam pembinaan }\\ &\begin{aligned} & =112 \mathrm{~m}^2 \div 1 \mathrm{~m}^2 \\ & =112 \mathrm{keping} \end{aligned} \end{aligned} $$
(b)
Tidak boleh
112 bukan kuasa dua sempurna.
Soalan 10:
Hypatia ialah seorang ahli Matematik Mesir yang dilahirkan pada tahun 370 Masihi. Dalam satu kajian, Hypatia mengemukakan masalah berikut:
• Nombor ini ialah hasil tambah dua nombor kuasa dua.
• Kuasa dua nombor ini juga merupakan hasil tambah dua nombor kuasa dua.
Satu daripada nombor yang memuaskan kekangan yang ditetapkan oleh Hypatia ialah 5. Cari tiga nombor yang lain.
Penyelesaian:
$$ \begin{aligned} \text { Diberi } 5 & =1+4 \\ 5^2 & =9+16 \end{aligned} $$
$$ \begin{aligned} 10 & =1+9 \\ 10^2 & =36+64 \end{aligned} $$
$$ \begin{aligned} 13 & =4+9 \\ 13^2 & =25+144 \end{aligned} $$
$$ \begin{aligned} 17 & =1+16 \\ 17^2 & =64+225 \end{aligned} $$
$$ \begin{aligned} 20 & =4+16 \\ 20^2 & =144+256 \end{aligned} $$
$$ \begin{aligned} 40 & =4+36 \\ 40^2 & =576+1024 \end{aligned} $$
Pilih mana-mana tiga nombor
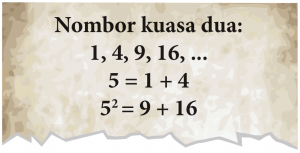
Hypatia ialah seorang ahli Matematik Mesir yang dilahirkan pada tahun 370 Masihi. Dalam satu kajian, Hypatia mengemukakan masalah berikut:
• Nombor ini ialah hasil tambah dua nombor kuasa dua.
• Kuasa dua nombor ini juga merupakan hasil tambah dua nombor kuasa dua.
Satu daripada nombor yang memuaskan kekangan yang ditetapkan oleh Hypatia ialah 5. Cari tiga nombor yang lain.
Penyelesaian:
$$ \begin{aligned} \text { Diberi } 5 & =1+4 \\ 5^2 & =9+16 \end{aligned} $$
$$ \begin{aligned} 10 & =1+9 \\ 10^2 & =36+64 \end{aligned} $$
$$ \begin{aligned} 13 & =4+9 \\ 13^2 & =25+144 \end{aligned} $$
$$ \begin{aligned} 17 & =1+16 \\ 17^2 & =64+225 \end{aligned} $$
$$ \begin{aligned} 20 & =4+16 \\ 20^2 & =144+256 \end{aligned} $$
$$ \begin{aligned} 40 & =4+36 \\ 40^2 & =576+1024 \end{aligned} $$
Pilih mana-mana tiga nombor