Soalan 6:
Luas tapak sebuah piramid yang berbentuk segi empat sama ialah 52 900 m2. Cari panjang sisi tapak piramid itu.
Penyelesaian:
Diberi tapak piramid adalah berbentuk segi empat sama, maka, √52 900 ialah kuasa dua sempurna.
$$ \begin{aligned} \sqrt{52900} & =\sqrt{230 \times 230} \\ & =230 \mathrm{~m} \end{aligned} $$
Luas tapak sebuah piramid yang berbentuk segi empat sama ialah 52 900 m2. Cari panjang sisi tapak piramid itu.
Penyelesaian:
Diberi tapak piramid adalah berbentuk segi empat sama, maka, √52 900 ialah kuasa dua sempurna.
$$ \begin{aligned} \sqrt{52900} & =\sqrt{230 \times 230} \\ & =230 \mathrm{~m} \end{aligned} $$
Soalan 7:
Anggarkan nilai bagi setiap yang berikut.
(a) 2972
(b) 51.92
(c) (– 0.038)2
(d) (–8.12)2
(e) √14
(f ) √220
(g) √8. 3
(h) √0. 5
Penyelesaian:
(a) 2972
297 adalah antara 200 dengan 300.
2972 adalah antara 2002 dengan 3002.
iaitu, 2972 adalah antara 40 000 dengan 90 000.
Maka, 2972 ≈ 90 000
Atau anggarkan secara terus 2972 ≈ 3002 ≈ 90 000
(b) 51.92 ≈ 502 ≈ 2 500
(c) (– 0.038)2
(– 0.038) adalah antara (-0.03) dengan (-0.04).
(– 0.038)2 adalah antara (-0.03)2 dengan (-0.04)2.
iaitu, (– 0.038)2 adalah antara 0.0009 dengan 0.0016.
Maka, (– 0.038)2 ≈ 0.0016
Atau anggarkan secara terus (– 0.038)2 ≈ (-0.04)2 ≈ 0.0016
(d) (–8.12)2 ≈ (–8)2 ≈ 64
(e) √14
14 adalah kuasa dua sempurna antara 9 dengan 16.
√14 adalah antara √9 dengan √16.
iaitu, √14 adalah antara 3 dengan 4.
Maka, √14 ≈ 4
(f )
$$ \begin{aligned} \sqrt{220} & \approx \sqrt{225} \\ & \approx \sqrt{15 \times 15} \\ & \approx 15 \end{aligned} $$
(g)
$$ \begin{aligned} \sqrt{8.3} & \approx \sqrt{9} \\ & \approx \sqrt{3 \times 3} \\ & \approx 3 \end{aligned} $$
(h)
$$ \begin{aligned} \sqrt{0.5} & \approx \sqrt{0.49} \\ & \approx \sqrt{0.7 \times 0.7} \\ & \approx 0.7 \end{aligned} $$
Anggarkan nilai bagi setiap yang berikut.
(a) 2972
(b) 51.92
(c) (– 0.038)2
(d) (–8.12)2
(e) √14
(f ) √220
(g) √8. 3
(h) √0. 5
Penyelesaian:
(a) 2972
297 adalah antara 200 dengan 300.
2972 adalah antara 2002 dengan 3002.
iaitu, 2972 adalah antara 40 000 dengan 90 000.
Maka, 2972 ≈ 90 000
Atau anggarkan secara terus 2972 ≈ 3002 ≈ 90 000
(b) 51.92 ≈ 502 ≈ 2 500
(c) (– 0.038)2
(– 0.038) adalah antara (-0.03) dengan (-0.04).
(– 0.038)2 adalah antara (-0.03)2 dengan (-0.04)2.
iaitu, (– 0.038)2 adalah antara 0.0009 dengan 0.0016.
Maka, (– 0.038)2 ≈ 0.0016
Atau anggarkan secara terus (– 0.038)2 ≈ (-0.04)2 ≈ 0.0016
(d) (–8.12)2 ≈ (–8)2 ≈ 64
(e) √14
14 adalah kuasa dua sempurna antara 9 dengan 16.
√14 adalah antara √9 dengan √16.
iaitu, √14 adalah antara 3 dengan 4.
Maka, √14 ≈ 4
(f )
$$ \begin{aligned} \sqrt{220} & \approx \sqrt{225} \\ & \approx \sqrt{15 \times 15} \\ & \approx 15 \end{aligned} $$
(g)
$$ \begin{aligned} \sqrt{8.3} & \approx \sqrt{9} \\ & \approx \sqrt{3 \times 3} \\ & \approx 3 \end{aligned} $$
(h)
$$ \begin{aligned} \sqrt{0.5} & \approx \sqrt{0.49} \\ & \approx \sqrt{0.7 \times 0.7} \\ & \approx 0.7 \end{aligned} $$
Soalan 8:
Seramai 100 orang ahli kebudayaan telah menyertai Perarakan Citrawarna Malaysia. Mereka membuat formasi pelbagai bentuk sepanjang perarakan itu.
(a) Apabila kumpulan ahli kebudayaan membuat formasi yang berbentuk segi empat sama, nyatakan bilangan ahli yang ada pada setiap baris segi empat sama itu.
(b) Pada suatu ketika, kumpulan ahli itu membentuk dua segi empat sama serentak.
Tentukan bilangan ahli pada setiap baris bagi setiap segi empat sama itu
Penyelesaian:
(a)
Untuk membentuk kuasa dua sempurna daripada 100 orang ahli,
bilangan ahli yang ada pada setiap baris segi empat
= √100
= √(10×10)
= 10 orang
(b)
Untuk membentuk dua segi empat sama daripada 100 orang ahli,
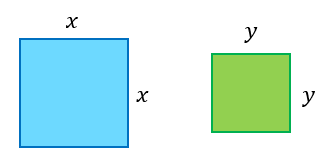
$$ \begin{aligned} (x \times x)+(y \times y) & =100 \\ x^2+y^2 & =100 \\ 8^2+6^2 & =100 \\ 64+36 & =100 \end{aligned} $$
Maka, terdapat 8 orang ahli dan 6 orang ahli masing-masing dalam setiap baris bagi segi empat sama pertama dan segi empat sama kedua.
Seramai 100 orang ahli kebudayaan telah menyertai Perarakan Citrawarna Malaysia. Mereka membuat formasi pelbagai bentuk sepanjang perarakan itu.
(a) Apabila kumpulan ahli kebudayaan membuat formasi yang berbentuk segi empat sama, nyatakan bilangan ahli yang ada pada setiap baris segi empat sama itu.
(b) Pada suatu ketika, kumpulan ahli itu membentuk dua segi empat sama serentak.
Tentukan bilangan ahli pada setiap baris bagi setiap segi empat sama itu
Penyelesaian:
(a)
Untuk membentuk kuasa dua sempurna daripada 100 orang ahli,
bilangan ahli yang ada pada setiap baris segi empat
= √100
= √(10×10)
= 10 orang
(b)
Untuk membentuk dua segi empat sama daripada 100 orang ahli,

$$ \begin{aligned} (x \times x)+(y \times y) & =100 \\ x^2+y^2 & =100 \\ 8^2+6^2 & =100 \\ 64+36 & =100 \end{aligned} $$
Maka, terdapat 8 orang ahli dan 6 orang ahli masing-masing dalam setiap baris bagi segi empat sama pertama dan segi empat sama kedua.