Soalan 12:
Amy akan meletakkan sebiji bola di puncak tiang seperti dalam Rajah di bawah. Jadual di bawah menunjukkan diameter bagi tiga biji bola X, Y dan Z.
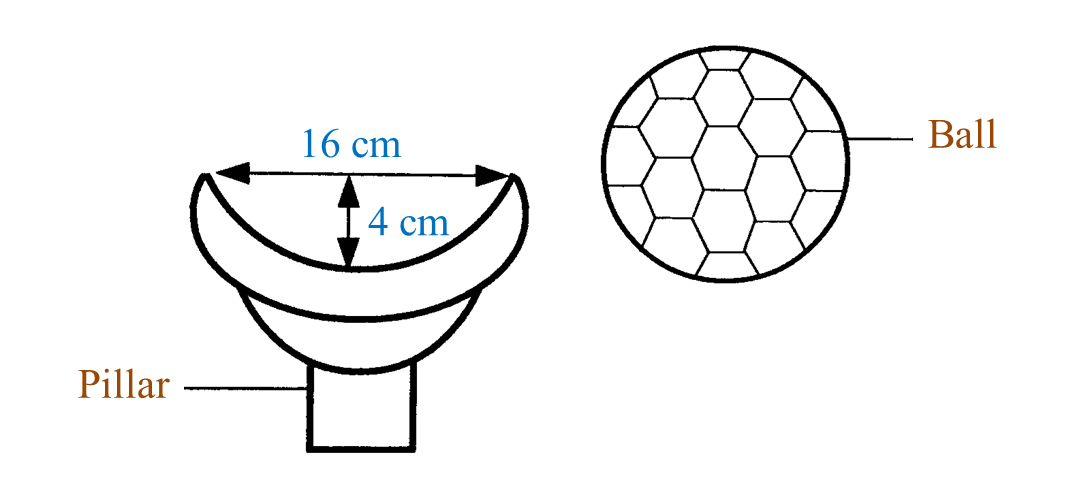
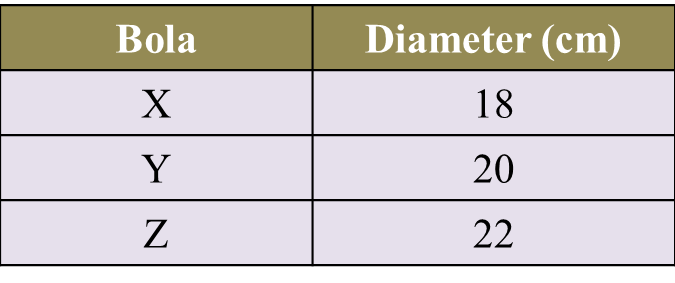
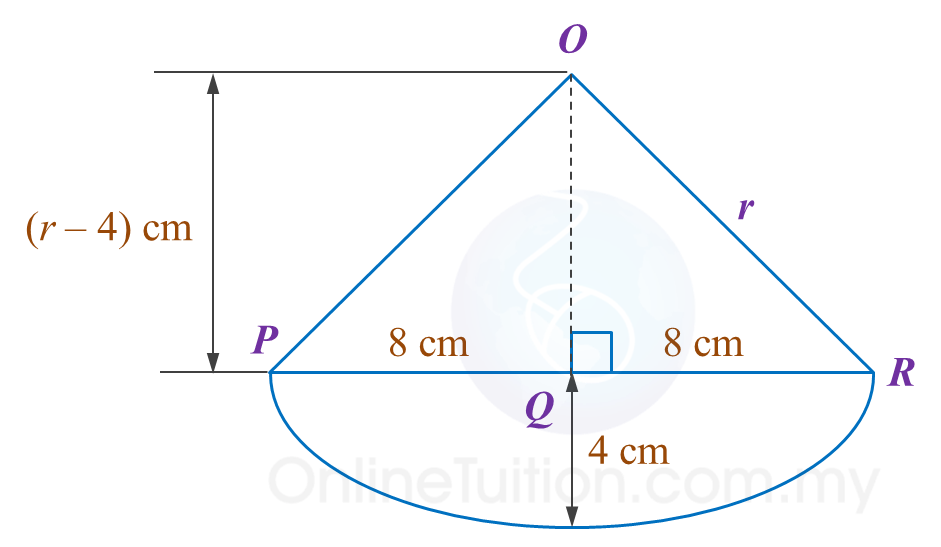
Antara bola X, Y atau Z, yang manakah muat dengan sempurna di puncak tiang itu? Tunjukkan pengiraan bagi menyokong pilihan Amy.
Penyelesaian:
Amy akan meletakkan sebiji bola di puncak tiang seperti dalam Rajah di bawah. Jadual di bawah menunjukkan diameter bagi tiga biji bola X, Y dan Z.


Antara bola X, Y atau Z, yang manakah muat dengan sempurna di puncak tiang itu? Tunjukkan pengiraan bagi menyokong pilihan Amy.
Penyelesaian:

Soalan 13:
Rajah di bawah menunjukkan rim roda sebuah basikal yang berdiameter 26 cm. Kenny bercadang membina sebuah pemegang untuk rim itu.
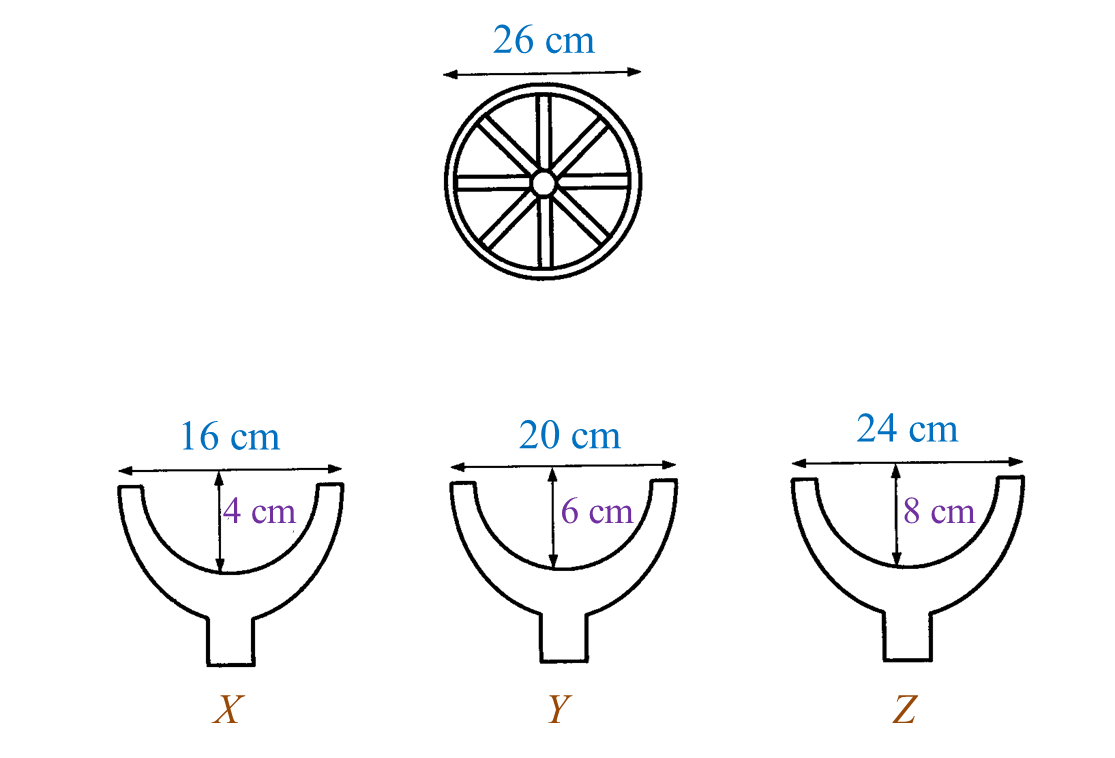
Antara pemegang rim , X, Y atau Z, yang manakah dapat memuatkan rim itu dengan sempurna? Tunjukkan pengiraan bagi menyokong jawapan anda.
Penyelesaian:
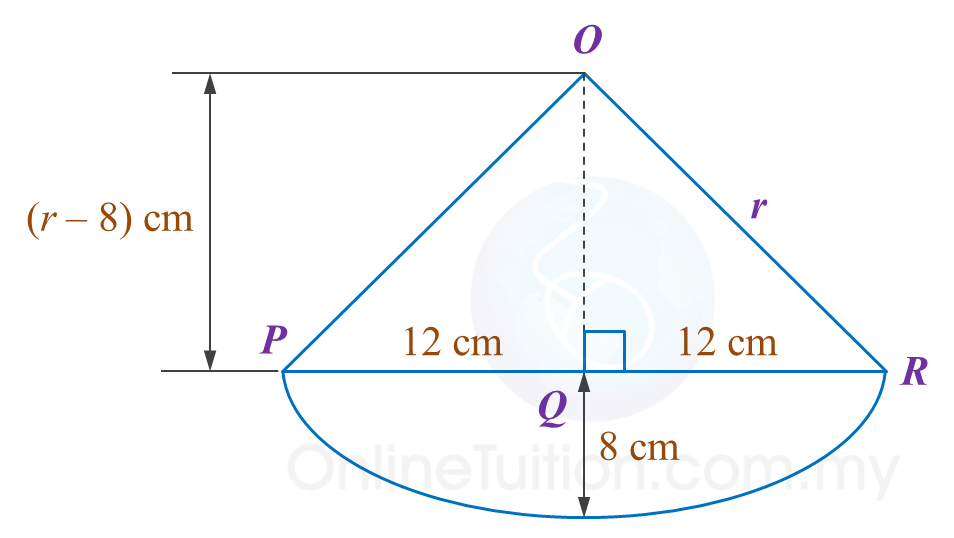
Rajah di bawah menunjukkan rim roda sebuah basikal yang berdiameter 26 cm. Kenny bercadang membina sebuah pemegang untuk rim itu.

Antara pemegang rim , X, Y atau Z, yang manakah dapat memuatkan rim itu dengan sempurna? Tunjukkan pengiraan bagi menyokong jawapan anda.
Penyelesaian:
