Soalan 1:
Jadual menunjukkan bilangan anak bagi 40 buah keluarga dalam satu program motivasi.
Penyelesaian:
Jadual menunjukkan bilangan anak bagi 40 buah keluarga dalam satu program motivasi.

Kenal pasti mod.
Penyelesaian:

Soalan 2:
Min bagi tujuh nombor ialah 10. Lima daripada nombor itu ialah 6, 5, 14, 10 dan 11. Dua lagi nombor masing-masing diwakili dengan k. Hitung
(a) jumlah tujuh nombor tersebut.
(b) nilai bagi k.
Min bagi tujuh nombor ialah 10. Lima daripada nombor itu ialah 6, 5, 14, 10 dan 11. Dua lagi nombor masing-masing diwakili dengan k. Hitung
(a) jumlah tujuh nombor tersebut.
(b) nilai bagi k.
Penyelesaian:
(a)
$$
\begin{aligned}
\text { Jumlah tujuh nombor } & =7 \times 10 \\
& =70
\end{aligned}
$$
(b)
$$
\begin{aligned}
\operatorname{Min} & =\frac{6+5+14+10+11+k+k}{7} \\
10 & =\frac{46+2 \mathrm{k}}{7} \\
70 & =46+2 \mathrm{k} \\
-2 \mathrm{k} & =46-70 \\
-2 \mathrm{k} & =-24 \\
k & =\frac{-24}{-2} \\
k & =12
\end{aligned}
$$
Soalan 3:
Hitung min bagi setiap perwakilan data berikut.
Penyelesaian:
(a)
$$
\begin{aligned}
\operatorname{Min} & =\frac{72+73+81+81+84+85+92+96}{8} \\
& =\frac{664}{8} \\
& =83 \text { markah }
\end{aligned}
$$
(b)
$$
\begin{aligned}
\operatorname{Min} & =\frac{(1 \times 6)+(4 \times 7)+(2 \times 8)+(3 \times 9)+(1 \times 10)}{1+4+2+3+1} \\
& =\frac{87}{11} \\
& =7.91 \\
& \approx 8 \text { bungkusan }
\end{aligned}
$$
Hitung min bagi setiap perwakilan data berikut.

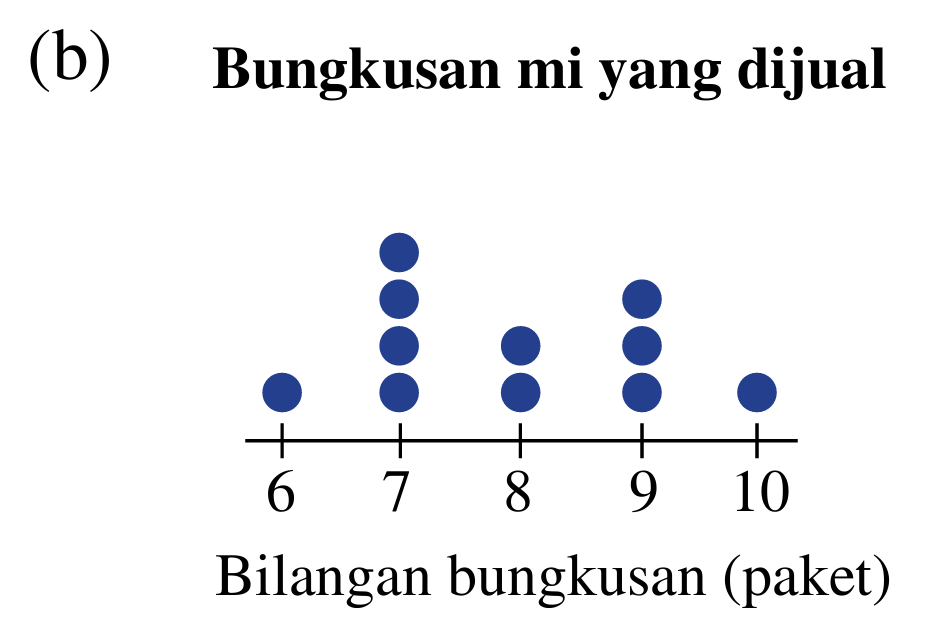
Penyelesaian:
(a)
$$
\begin{aligned}
\operatorname{Min} & =\frac{72+73+81+81+84+85+92+96}{8} \\
& =\frac{664}{8} \\
& =83 \text { markah }
\end{aligned}
$$
(b)
$$
\begin{aligned}
\operatorname{Min} & =\frac{(1 \times 6)+(4 \times 7)+(2 \times 8)+(3 \times 9)+(1 \times 10)}{1+4+2+3+1} \\
& =\frac{87}{11} \\
& =7.91 \\
& \approx 8 \text { bungkusan }
\end{aligned}
$$
Soalan 4:
Jadual menunjukkan markah ujian kelayakan peserta kuiz Sejarah yang diperoleh sekumpulan murid. Hitung median.
Penyelesaian:
$$
\begin{aligned}
\text { Jumlah kekerapan } & =2+7+5+11+9+7 \\
& =41 \text { (Nombor ganjil) }
\end{aligned}
$$
$$
\begin{aligned}
\text { Median } & =\text { Purata data ke }-\left(\frac{41+1}{2}\right) \\
& =\text { data ke-21 }
\end{aligned}
$$

Jadual menunjukkan markah ujian kelayakan peserta kuiz Sejarah yang diperoleh sekumpulan murid. Hitung median.

Penyelesaian:
$$
\begin{aligned}
\text { Jumlah kekerapan } & =2+7+5+11+9+7 \\
& =41 \text { (Nombor ganjil) }
\end{aligned}
$$
$$
\begin{aligned}
\text { Median } & =\text { Purata data ke }-\left(\frac{41+1}{2}\right) \\
& =\text { data ke-21 }
\end{aligned}
$$

Median markah = 20