Soalan 5:
Seorang pelukis ingin membuat lukisan penuh pada permukaan sebuah tembikar hiasan yang berbentuk silinder. Tembikar berbentuk silinder tersebut mempunyai ketinggian 10 cm dan jejari 3.5 cm. Jika satu tiub warna dapat menghasilkan lukisan seluas 100 cm2, berapakah bilangan tiub warna yang diperlukan untuk membuat lukisan penuh pada 10 buah tembikar yang sama jenis?
Penyelesaian:
$$ \begin{aligned} \text { Luas permukaan silinder } & =2 \pi j^2+2 \pi j t \\ & =\left(2 \times \frac{22}{7} \times 3.5^2\right)+\left(2 \times \frac{22}{7} \times 3.5 \times 10\right) \\ & =77+220 \\ & =297 \mathrm{~cm}^2 \end{aligned} $$
Bilangan tiub warna yang diperlukan untuk membuat lukisan penuh pada 10 buah tembikar yang sama jenis $$ \begin{aligned} & =\left(297 \mathrm{~cm}^2 \times 10\right) \div 100 \mathrm{~cm}^2 \\ & =29.7 \\ & \approx 30 \text { tiub warna } \end{aligned} $$
Seorang pelukis ingin membuat lukisan penuh pada permukaan sebuah tembikar hiasan yang berbentuk silinder. Tembikar berbentuk silinder tersebut mempunyai ketinggian 10 cm dan jejari 3.5 cm. Jika satu tiub warna dapat menghasilkan lukisan seluas 100 cm2, berapakah bilangan tiub warna yang diperlukan untuk membuat lukisan penuh pada 10 buah tembikar yang sama jenis?
Penyelesaian:
$$ \begin{aligned} \text { Luas permukaan silinder } & =2 \pi j^2+2 \pi j t \\ & =\left(2 \times \frac{22}{7} \times 3.5^2\right)+\left(2 \times \frac{22}{7} \times 3.5 \times 10\right) \\ & =77+220 \\ & =297 \mathrm{~cm}^2 \end{aligned} $$
Bilangan tiub warna yang diperlukan untuk membuat lukisan penuh pada 10 buah tembikar yang sama jenis $$ \begin{aligned} & =\left(297 \mathrm{~cm}^2 \times 10\right) \div 100 \mathrm{~cm}^2 \\ & =29.7 \\ & \approx 30 \text { tiub warna } \end{aligned} $$
Soalan 6:
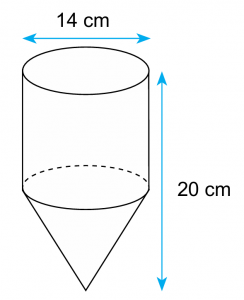
Rajah di sebelah menunjukkan gabungan silinder dan kon. 1/2kg gula dapat menghasilkan 1 liter air gula untuk dibuat manisan mengikut bentuk tersebut. Jika tinggi silinder ialah dua kali jejari silinder, berapakah jumlah manisan yang dapat dihasilkan dengan 100 kg gula?
Penyelesaian:
$$ \text { Jejari silinder }=14 \mathrm{~cm} \div 2=7 \mathrm{~cm} $$
$$ \text { Tinggi silinder }=2 \times 7 \mathrm{~cm}=14 \mathrm{~cm} $$
$$ \text { Tinggi kon }=20 \mathrm{~cm}-14 \mathrm{~cm}=6 \mathrm{~cm} $$
$$ \begin{aligned} &\text { Isipadu seketul manisan }\\ &\begin{aligned} & =\left(\frac{22}{7} \times 7^2 \times 14\right)+\left(\frac{1}{3} \times \frac{22}{7} \times 7^2 \times 6\right) \\ & =2156+308 \\ & =2464 \mathrm{~cm}^3 \end{aligned} \end{aligned} $$
Diberi ½ kg gula menghasilkan 1 liter air gula.
100 kg gula dapat menghasilkan 200 liter = 200 000 cm3 air gula.
$$ \begin{aligned} &\text { Jumlah manisan yang dapat dihasilkan dengan } 100 \text { kg gula }\\ &\begin{aligned} & =200000 \mathrm{~cm}^3 \div 2464 \mathrm{~cm}^3 \\ & =81.16 \\ & =81 \text { ketul manisan } \end{aligned} \end{aligned} $$
Rajah di sebelah menunjukkan gabungan silinder dan kon. 1/2kg gula dapat menghasilkan 1 liter air gula untuk dibuat manisan mengikut bentuk tersebut. Jika tinggi silinder ialah dua kali jejari silinder, berapakah jumlah manisan yang dapat dihasilkan dengan 100 kg gula?

Penyelesaian:
$$ \text { Jejari silinder }=14 \mathrm{~cm} \div 2=7 \mathrm{~cm} $$
$$ \text { Tinggi silinder }=2 \times 7 \mathrm{~cm}=14 \mathrm{~cm} $$
$$ \text { Tinggi kon }=20 \mathrm{~cm}-14 \mathrm{~cm}=6 \mathrm{~cm} $$
$$ \begin{aligned} &\text { Isipadu seketul manisan }\\ &\begin{aligned} & =\left(\frac{22}{7} \times 7^2 \times 14\right)+\left(\frac{1}{3} \times \frac{22}{7} \times 7^2 \times 6\right) \\ & =2156+308 \\ & =2464 \mathrm{~cm}^3 \end{aligned} \end{aligned} $$
Diberi ½ kg gula menghasilkan 1 liter air gula.
100 kg gula dapat menghasilkan 200 liter = 200 000 cm3 air gula.
$$ \begin{aligned} &\text { Jumlah manisan yang dapat dihasilkan dengan } 100 \text { kg gula }\\ &\begin{aligned} & =200000 \mathrm{~cm}^3 \div 2464 \mathrm{~cm}^3 \\ & =81.16 \\ & =81 \text { ketul manisan } \end{aligned} \end{aligned} $$
Soalan 7:
Sebuah silinder terbuka di bahagian atas dengan ketinggian dua kali jejari tapaknya, diisikan air sehingga tiga perempat penuh. Sebanyak 539 ml air diperlukan lagi untuk memenuhkan silinder tersebut. Hitung luas, dalam unit cm2, permukaan silinder. (Guna π = 22/7 )
Penyelesaian:
Diberi 539 ml = ¼ daripada air dalam silinder
Isipadu silinder penuh = 539 × 4 = 2156 ml
Katakan jejari tapak = y
Tinggi silinder = 2y
$$ \begin{aligned} &\text { Isipadu silinder }=\pi j^2 t\\ &\begin{aligned} \frac{22}{7} \times y^2 \times 2 y & =2156 \\ \frac{44}{7} y^3 & =2156 \\ y^3 & =2156 \times \frac{7}{44} \\ y^3 & =343 \\ y & =\sqrt[3]{343} \\ y & =7 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Luas permukaan silinder }\\ &\begin{aligned} & =\pi j^2+2 \pi j t \\ & =\left(\frac{22}{7} \times 7^2\right)+\left(2 \times \frac{22}{7} \times 7 \times 14\right) \\ & =154+616 \\ & =770 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
Sebuah silinder terbuka di bahagian atas dengan ketinggian dua kali jejari tapaknya, diisikan air sehingga tiga perempat penuh. Sebanyak 539 ml air diperlukan lagi untuk memenuhkan silinder tersebut. Hitung luas, dalam unit cm2, permukaan silinder. (Guna π = 22/7 )
Penyelesaian:
Diberi 539 ml = ¼ daripada air dalam silinder
Isipadu silinder penuh = 539 × 4 = 2156 ml
Katakan jejari tapak = y
Tinggi silinder = 2y
$$ \begin{aligned} &\text { Isipadu silinder }=\pi j^2 t\\ &\begin{aligned} \frac{22}{7} \times y^2 \times 2 y & =2156 \\ \frac{44}{7} y^3 & =2156 \\ y^3 & =2156 \times \frac{7}{44} \\ y^3 & =343 \\ y & =\sqrt[3]{343} \\ y & =7 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Luas permukaan silinder }\\ &\begin{aligned} & =\pi j^2+2 \pi j t \\ & =\left(\frac{22}{7} \times 7^2\right)+\left(2 \times \frac{22}{7} \times 7 \times 14\right) \\ & =154+616 \\ & =770 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
Soalan 8:
Rajah di bawah menunjukkan satu bongkah kon dan satu bongkah piramid. Isi padu piramid ialah tiga kali ganda isi padu kon. Luas tapak piramid ialah dua kali ganda luas tapak kon.
Hitung jumlah tinggi kon dan tinggi piramid, jika tinggi kon ialah 18 cm. (Guna π = 22/7)
Penyelesaian:
Katakan luas tapak kon = A,
maka luas tapak piramid = 2A
$$ \begin{aligned} \text { Isi padu kon, } I_1 & =\frac{1}{3} A h_1 \\ \text { Isi padu piramid, } I_2 & =\frac{1}{3}(2 A) h_2 \\ \text { Diberi } I_2 & =3 I_1 \\ \frac{1}{3}(2 A) h_2 & =3\left(\frac{1}{3} A h_1\right) \\ h_2 & =\frac{3}{2} h_1 \\ h_2 & =\frac{3}{2}(18) \\ h_2 & =27 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} \text { Jumlah tinggi } & =h_1+h_2 \\ & =18 \mathrm{~cm}+27 \mathrm{~cm} \\ & =45 \mathrm{~cm} \end{aligned} $$
Rajah di bawah menunjukkan satu bongkah kon dan satu bongkah piramid. Isi padu piramid ialah tiga kali ganda isi padu kon. Luas tapak piramid ialah dua kali ganda luas tapak kon.
Hitung jumlah tinggi kon dan tinggi piramid, jika tinggi kon ialah 18 cm. (Guna π = 22/7)

Penyelesaian:
Katakan luas tapak kon = A,
maka luas tapak piramid = 2A
$$ \begin{aligned} \text { Isi padu kon, } I_1 & =\frac{1}{3} A h_1 \\ \text { Isi padu piramid, } I_2 & =\frac{1}{3}(2 A) h_2 \\ \text { Diberi } I_2 & =3 I_1 \\ \frac{1}{3}(2 A) h_2 & =3\left(\frac{1}{3} A h_1\right) \\ h_2 & =\frac{3}{2} h_1 \\ h_2 & =\frac{3}{2}(18) \\ h_2 & =27 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} \text { Jumlah tinggi } & =h_1+h_2 \\ & =18 \mathrm{~cm}+27 \mathrm{~cm} \\ & =45 \mathrm{~cm} \end{aligned} $$