Soalan 6:
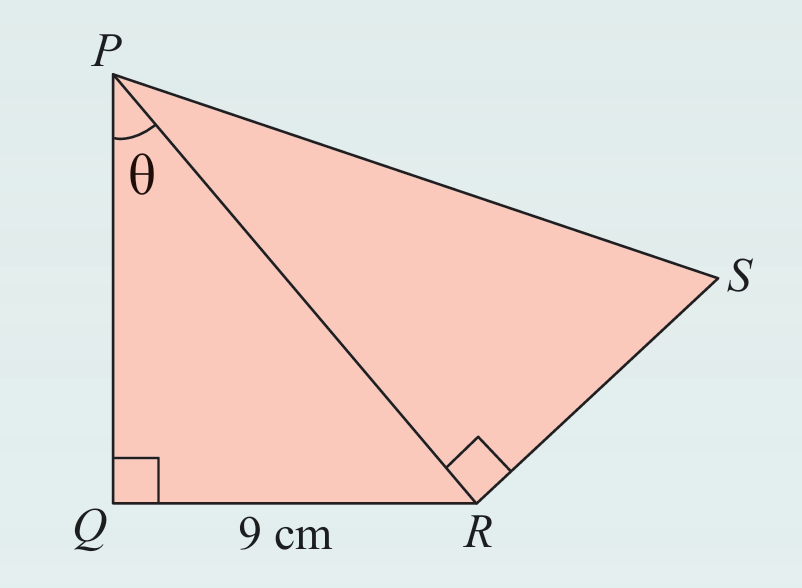
Rajah di sebelah menunjukkan segi tiga bersudut tegak PQR dan PRS. Diberi bahawa tan θ = 3/4 dan PS = 3/5 PR.
Hitung panjang, dalam cm,
(a) PR
(b) RS
Penyelesaian:
(a)
$$ \text { Diberi } \tan \theta=\frac{3}{4} $$
$$ \begin{aligned} \tan \theta & =\frac{\text { sisi bertentangan }(0)}{\text { sisi bersebelahan }(\mathrm{A})} \\ \frac{Q R}{P Q} & =\frac{3}{4} \\ \frac{9}{P Q} & =\frac{3}{4} \\ 9 \times \frac{4}{3} & =P Q \\ 12 & =P Q \\ P Q & =12 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} &\text { Guna teorem Pythagoras }\\ &\begin{aligned} P R^2 & =P Q^2+Q R^2 \\ P R & =\sqrt{12^2+9^2} \\ & =\sqrt{225} \\ & =15 \mathrm{~cm} \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} \text { Diberi } P S & =\frac{5}{3} P R \\ P S & =\frac{5}{3}(15 \mathrm{~cm}) \\ & =25 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} &\text { Guna teorem Pythagoras }\\ &\begin{aligned} R S^2 & =P S^2-P R^2 \\ R S & =\sqrt{25^2-15^2} \\ & =\sqrt{400} \\ & =20 \mathrm{~cm} \end{aligned} \end{aligned} $$

Rajah di sebelah menunjukkan segi tiga bersudut tegak PQR dan PRS. Diberi bahawa tan θ = 3/4 dan PS = 3/5 PR.
Hitung panjang, dalam cm,
(a) PR
(b) RS
Penyelesaian:
(a)
$$ \text { Diberi } \tan \theta=\frac{3}{4} $$
$$ \begin{aligned} \tan \theta & =\frac{\text { sisi bertentangan }(0)}{\text { sisi bersebelahan }(\mathrm{A})} \\ \frac{Q R}{P Q} & =\frac{3}{4} \\ \frac{9}{P Q} & =\frac{3}{4} \\ 9 \times \frac{4}{3} & =P Q \\ 12 & =P Q \\ P Q & =12 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} &\text { Guna teorem Pythagoras }\\ &\begin{aligned} P R^2 & =P Q^2+Q R^2 \\ P R & =\sqrt{12^2+9^2} \\ & =\sqrt{225} \\ & =15 \mathrm{~cm} \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} \text { Diberi } P S & =\frac{5}{3} P R \\ P S & =\frac{5}{3}(15 \mathrm{~cm}) \\ & =25 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} &\text { Guna teorem Pythagoras }\\ &\begin{aligned} R S^2 & =P S^2-P R^2 \\ R S & =\sqrt{25^2-15^2} \\ & =\sqrt{400} \\ & =20 \mathrm{~cm} \end{aligned} \end{aligned} $$
Soalan 7:
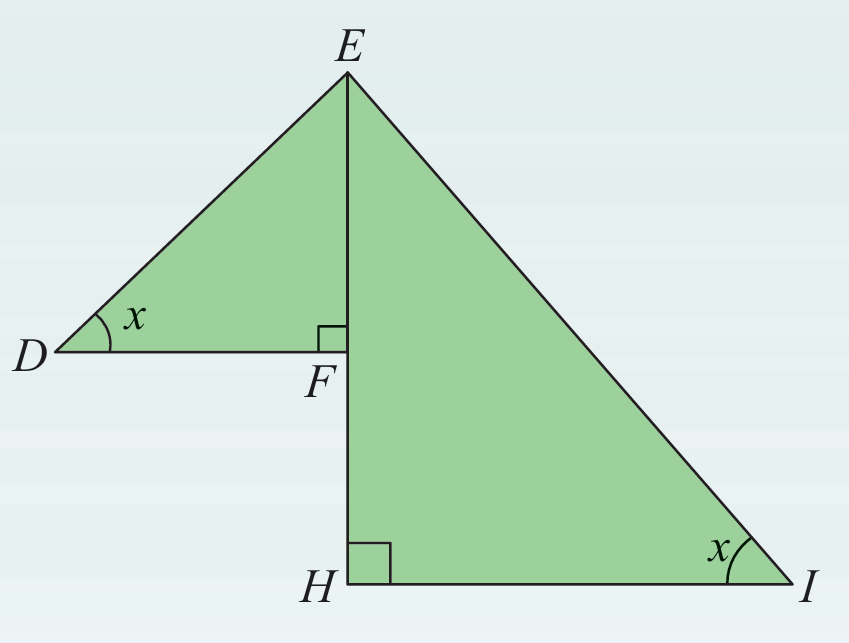
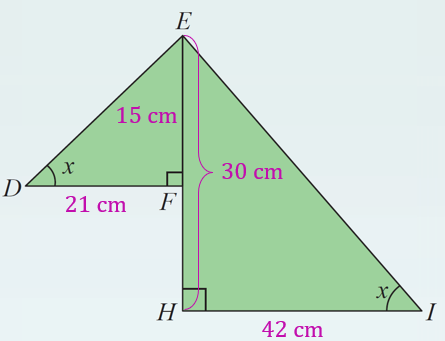
Rajah di sebelah menunjukkan segi tiga bersudut tegak DFE dan EHI. Jika tan x = 5/7, panjang DF = 21 cm dan nisbah panjang EF : EH = 1 : 2, tentukan panjang EI dalam cm.
Penyelesaian:
$$ \text { Diberi } \tan x=\frac{5}{7} $$
$$ \tan \theta=\frac{\text { sisi bertentangan }(0)}{\text { sisi bersebelahan }(\mathrm{A})} $$
$$ \begin{aligned} &\text { Bagi } \triangle D E F \text {, }\\ &\begin{aligned} \frac{E F}{D F} & =\frac{5}{7} \\ \frac{E F}{21} & =\frac{5}{7} \\ E F & =\frac{5}{7} \times 21 \\ & =15 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Diberi } E F: E H=1: 2\\ &\begin{aligned} \frac{E F}{E H} & =\frac{1}{2} \\ \frac{15}{E H} & =\frac{1}{2} \\ 15 \times 2 & =E H \\ E H & =30 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Bagi } \triangle E H I, \tan x=\frac{5}{7} \\ \frac{E H}{H I}=\frac{5}{7} \\ \frac{30}{H I}=\frac{5}{7} \\ 30 \times \frac{7}{5}=H I \\ H I=42 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} &\text { Guna teorem Pythagoras }\\ &\begin{aligned} E I^2 & =E H^2+H I^2 \\ E I & =\sqrt{30^2+42^2} \\ & =\sqrt{2664} \\ & =51.61 \mathrm{~cm} \end{aligned} \end{aligned} $$

Rajah di sebelah menunjukkan segi tiga bersudut tegak DFE dan EHI. Jika tan x = 5/7, panjang DF = 21 cm dan nisbah panjang EF : EH = 1 : 2, tentukan panjang EI dalam cm.
Penyelesaian:
$$ \text { Diberi } \tan x=\frac{5}{7} $$
$$ \tan \theta=\frac{\text { sisi bertentangan }(0)}{\text { sisi bersebelahan }(\mathrm{A})} $$
$$ \begin{aligned} &\text { Bagi } \triangle D E F \text {, }\\ &\begin{aligned} \frac{E F}{D F} & =\frac{5}{7} \\ \frac{E F}{21} & =\frac{5}{7} \\ E F & =\frac{5}{7} \times 21 \\ & =15 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Diberi } E F: E H=1: 2\\ &\begin{aligned} \frac{E F}{E H} & =\frac{1}{2} \\ \frac{15}{E H} & =\frac{1}{2} \\ 15 \times 2 & =E H \\ E H & =30 \mathrm{~cm} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Bagi } \triangle E H I, \tan x=\frac{5}{7} \\ \frac{E H}{H I}=\frac{5}{7} \\ \frac{30}{H I}=\frac{5}{7} \\ 30 \times \frac{7}{5}=H I \\ H I=42 \mathrm{~cm} \end{aligned} $$

$$ \begin{aligned} &\text { Guna teorem Pythagoras }\\ &\begin{aligned} E I^2 & =E H^2+H I^2 \\ E I & =\sqrt{30^2+42^2} \\ & =\sqrt{2664} \\ & =51.61 \mathrm{~cm} \end{aligned} \end{aligned} $$