Soalan 4:
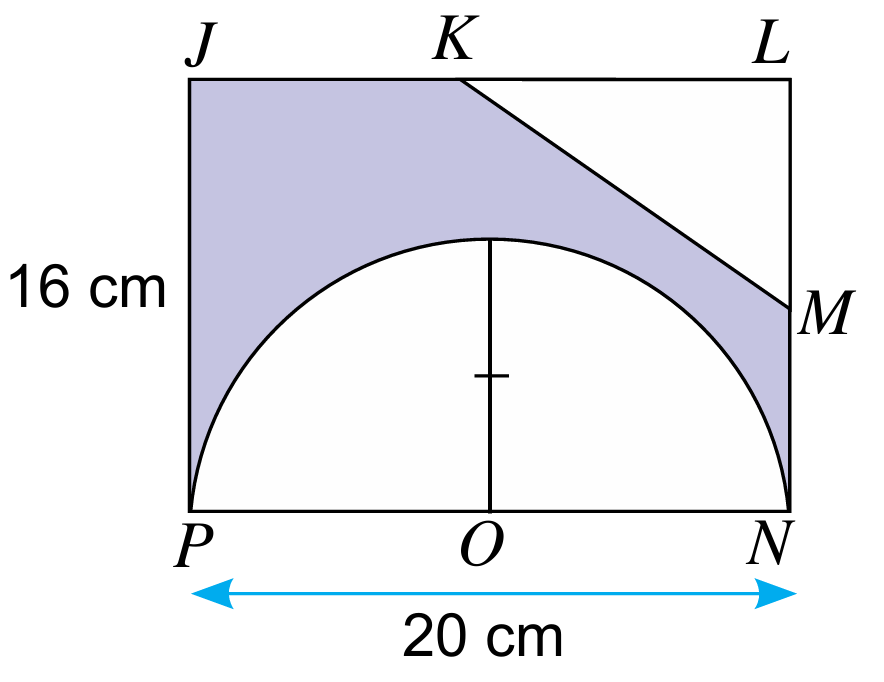
Rajah di sebelah menunjukkan sebidang tanah berbentuk segi empat tepat JLNP yang dimiliki oleh Encik Rashid. Encik Rashid telah membahagikan tanahnya kepada tiga bahagian. K ialah titik tengah bagi JL dan M ialah titik tengah bagi LN. Encik Rashid bercadang untuk menanam sayur di kawasan berbentuk segi tiga KLM dan semi bulatan. Hitung luas kawasan yang tidak ditanam dengan sayur. (Guna π = 3.142)
Penyelesaian:
$$ \begin{aligned} & K L=20 \div 2=10 \mathrm{~cm} \\ & L M=16 \div 2=8 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} & \text { Luas } \triangle K L M=\frac{1}{2} \times K L \times L M \\ & =\frac{1}{2} \times 10 \times 8 \\ & =40 \mathrm{~cm}^2 \end{aligned} $$
$$ \text { Jejari semi bulatan } P O N, j=10 \mathrm{~cm} $$
$$ \begin{aligned} & \text { Luas semi bulatan }=\frac{\theta}{360^{\circ}} \times \pi j^2 \\ & \begin{aligned} \text { Luas semi bulatan } P O N & =\left(\frac{180^{\circ}}{360^{\circ}}\right)(3.142)(10)^2 \\ & =157.1 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Luas tanah } & =20 \times 16 \\ & =320 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{aligned} &\text { Luas kawasan yang tidak ditanam dengan sayur }\\ &\begin{aligned} & =320-157.1-40 \\ & =122.9 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
Rajah di sebelah menunjukkan sebidang tanah berbentuk segi empat tepat JLNP yang dimiliki oleh Encik Rashid. Encik Rashid telah membahagikan tanahnya kepada tiga bahagian. K ialah titik tengah bagi JL dan M ialah titik tengah bagi LN. Encik Rashid bercadang untuk menanam sayur di kawasan berbentuk segi tiga KLM dan semi bulatan. Hitung luas kawasan yang tidak ditanam dengan sayur. (Guna π = 3.142)
Penyelesaian:
$$ \begin{aligned} & K L=20 \div 2=10 \mathrm{~cm} \\ & L M=16 \div 2=8 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} & \text { Luas } \triangle K L M=\frac{1}{2} \times K L \times L M \\ & =\frac{1}{2} \times 10 \times 8 \\ & =40 \mathrm{~cm}^2 \end{aligned} $$
$$ \text { Jejari semi bulatan } P O N, j=10 \mathrm{~cm} $$
$$ \begin{aligned} & \text { Luas semi bulatan }=\frac{\theta}{360^{\circ}} \times \pi j^2 \\ & \begin{aligned} \text { Luas semi bulatan } P O N & =\left(\frac{180^{\circ}}{360^{\circ}}\right)(3.142)(10)^2 \\ & =157.1 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Luas tanah } & =20 \times 16 \\ & =320 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{aligned} &\text { Luas kawasan yang tidak ditanam dengan sayur }\\ &\begin{aligned} & =320-157.1-40 \\ & =122.9 \mathrm{~cm}^2 \end{aligned} \end{aligned} $$
Soalan 5:
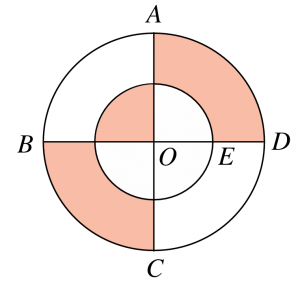
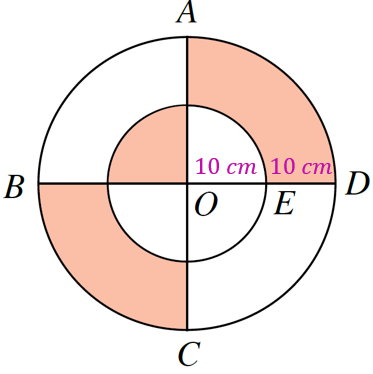
Kevin ingin membina satu papan panahan yang berbentuk bulatan. Papan panahan tersebut terdiri daripada dua bulatan yang berpusat di O dan tiga sektor yang berlorek seperti rajah di sebelah. Diameter BOD dan AOC adalah berserenjang antara satu sama lain. Diberi OE = ED = 10 cm. Hitung luas, dalam cm2, kawasan berlorek. (Guna π = 22/7)
Penyelesaian:
$$
\begin{aligned}
\text { Luas sukuan bagi bulatan kecil } & =\left(\frac{90^{\circ}}{360^{\circ}}\right)\left(\frac{22}{7}\right)(10)^2 \\
& =\frac{550}{7} \mathrm{~cm}^2
\end{aligned}
$$
$$ \begin{aligned} \text { Luas sukuan bagi bulatan besar } & =\left(\frac{90^{\circ}}{360^{\circ}}\right)\left(\frac{22}{7}\right)(10+10)^2 \\ & =\frac{2200}{7} \mathrm{~cm}^2 \end{aligned} $$
Luas kawasan berlorek
= Luas sukuan AOD + Luas sukuan BOC – Luas sukuan bulatan kecil
$$ \begin{aligned} & =\frac{2200}{7}+\frac{2200}{7}-\frac{550}{7} \\ & =550 \mathrm{~cm}^2 \end{aligned} $$
Kevin ingin membina satu papan panahan yang berbentuk bulatan. Papan panahan tersebut terdiri daripada dua bulatan yang berpusat di O dan tiga sektor yang berlorek seperti rajah di sebelah. Diameter BOD dan AOC adalah berserenjang antara satu sama lain. Diberi OE = ED = 10 cm. Hitung luas, dalam cm2, kawasan berlorek. (Guna π = 22/7)
Penyelesaian:
$$
\begin{aligned}
\text { Luas sukuan bagi bulatan kecil } & =\left(\frac{90^{\circ}}{360^{\circ}}\right)\left(\frac{22}{7}\right)(10)^2 \\
& =\frac{550}{7} \mathrm{~cm}^2
\end{aligned}
$$$$ \begin{aligned} \text { Luas sukuan bagi bulatan besar } & =\left(\frac{90^{\circ}}{360^{\circ}}\right)\left(\frac{22}{7}\right)(10+10)^2 \\ & =\frac{2200}{7} \mathrm{~cm}^2 \end{aligned} $$
Luas kawasan berlorek
= Luas sukuan AOD + Luas sukuan BOC – Luas sukuan bulatan kecil
$$ \begin{aligned} & =\frac{2200}{7}+\frac{2200}{7}-\frac{550}{7} \\ & =550 \mathrm{~cm}^2 \end{aligned} $$
Soalan 6:
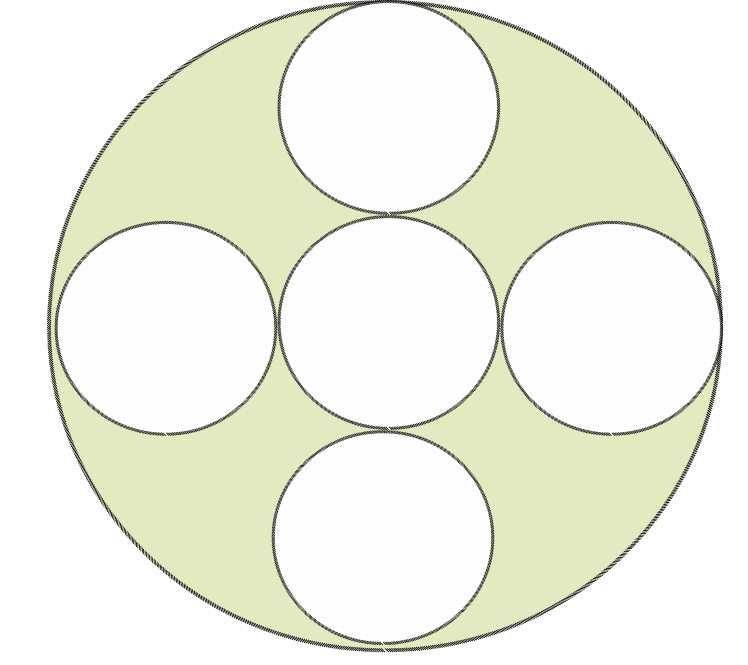
Di sebuah muzium terdapat tingkap berbentuk bulat yang dihiasi dengan gelung bulatan yang sama saiz seperti rajah di sebelah. Jejari tingkap tersebut ialah 45 cm. Hitung luas kawasan yang tidak dilitupi hiasan tersebut. (Guna π = 3.142)
Penyelesaian:
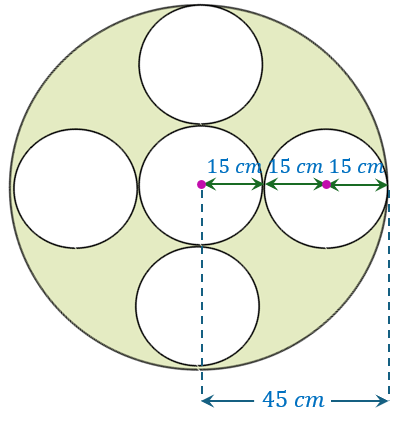
$$ \begin{aligned} \text { Luas tingkap } & =\pi j_1{ }^2 \\ & =(3.142)(45)^2 \\ & =6362.55 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{aligned} \text { Jejari gelung bulatan } & =\left(\frac{1}{3}\right)(45) \\ & =15 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} \text { Luas } 5 \text { gelung bulatan } & =5 \pi j_2{ }^2 \\ & =5(3.142)(15)^2 \\ & =3534.75 \mathrm{~cm}^2 \end{aligned} $$
Luas kawasan yang tidak dilitupi hiasan
= Luas tingkap – Luas 5 gelung bulatan
= 6362.55 – 3534.75
= 2827.8 cm2
Di sebuah muzium terdapat tingkap berbentuk bulat yang dihiasi dengan gelung bulatan yang sama saiz seperti rajah di sebelah. Jejari tingkap tersebut ialah 45 cm. Hitung luas kawasan yang tidak dilitupi hiasan tersebut. (Guna π = 3.142)
Penyelesaian:
$$ \begin{aligned} \text { Luas tingkap } & =\pi j_1{ }^2 \\ & =(3.142)(45)^2 \\ & =6362.55 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{aligned} \text { Jejari gelung bulatan } & =\left(\frac{1}{3}\right)(45) \\ & =15 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} \text { Luas } 5 \text { gelung bulatan } & =5 \pi j_2{ }^2 \\ & =5(3.142)(15)^2 \\ & =3534.75 \mathrm{~cm}^2 \end{aligned} $$
Luas kawasan yang tidak dilitupi hiasan
= Luas tingkap – Luas 5 gelung bulatan
= 6362.55 – 3534.75
= 2827.8 cm2