Soalan 4:
Suatu poligon sekata dengan sudut peluaran 36° dilukis semula dengan menggunakan skala 1 : 5. Jika panjang sebenar sisi poligon sekata itu ialah 10 cm, hitung perimeter lukisan berskala poligon sekata itu.
Penyelesaian:
$$ \begin{aligned} &\text { Bilangan sisi poligon sekata, } n\\ &\begin{aligned} & =\frac{360^{\circ}}{\text { Sudut peluaran }} \\ & =\frac{360^{\circ}}{36^{\circ}} \\ & =10 \mathrm{ sisi} \end{aligned} \end{aligned} $$
Poligon sekata ini mempunyai 10 sisi. Maka ia adalah sebuah dekagon.
$$ \begin{aligned} \text { Skala } & =\frac{\text { Sisi lukisan berskala }}{\text { Panjang sebenar sisi }} \\ \frac{1}{5} & =\frac{\text { Sisi lukisan berskala }}{10 \mathrm{~cm}} \\ \text { Sisi lukisan berskala } & =\frac{1}{5} \times 10 \mathrm{~cm} \\ & =2 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} &\text { Perimeter lukisan berskala poligon sekata }\\ &\begin{aligned} & =10(\text { sisi }) \times 2 \mathrm{~cm} \\ & =20 \mathrm{~cm} \end{aligned} \end{aligned} $$
Suatu poligon sekata dengan sudut peluaran 36° dilukis semula dengan menggunakan skala 1 : 5. Jika panjang sebenar sisi poligon sekata itu ialah 10 cm, hitung perimeter lukisan berskala poligon sekata itu.
Penyelesaian:
$$ \begin{aligned} &\text { Bilangan sisi poligon sekata, } n\\ &\begin{aligned} & =\frac{360^{\circ}}{\text { Sudut peluaran }} \\ & =\frac{360^{\circ}}{36^{\circ}} \\ & =10 \mathrm{ sisi} \end{aligned} \end{aligned} $$
Poligon sekata ini mempunyai 10 sisi. Maka ia adalah sebuah dekagon.
$$ \begin{aligned} \text { Skala } & =\frac{\text { Sisi lukisan berskala }}{\text { Panjang sebenar sisi }} \\ \frac{1}{5} & =\frac{\text { Sisi lukisan berskala }}{10 \mathrm{~cm}} \\ \text { Sisi lukisan berskala } & =\frac{1}{5} \times 10 \mathrm{~cm} \\ & =2 \mathrm{~cm} \end{aligned} $$
$$ \begin{aligned} &\text { Perimeter lukisan berskala poligon sekata }\\ &\begin{aligned} & =10(\text { sisi }) \times 2 \mathrm{~cm} \\ & =20 \mathrm{~cm} \end{aligned} \end{aligned} $$
Soalan 5:
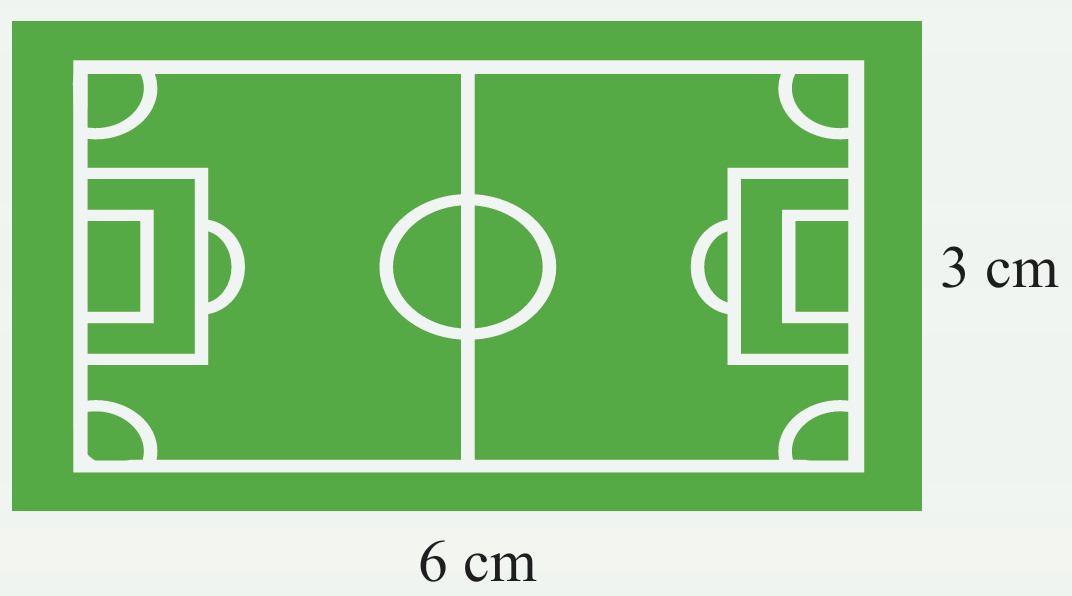
Rajah di atas menunjukkan lukisan berskala bagi sebuah padang yang berbentuk segi empat tepat.
(a) Jika skala yang digunakan ialah 1 : 2 000, hitung luas sebenar padang itu dalam meter persegi.
(b) Encik Dany memotong rumput di padang tersebut dengan kadar 400 meter persegi dalam masa 8 minit. Hitung tempoh masa, dalam jam dan minit, yang diperlukan oleh Encik Dany untuk memotong rumput keseluruhan padang tersebut.
Penyelesaian:
(a)
$$ \text { Skala }=\frac{\text { Sisi lukisan berskala }}{\text { Sisi objek yang sepadan }} $$
$$ \begin{aligned} \frac{1}{2000} & =\frac{6 \mathrm{~cm}}{\text { Panjang sebenar padang }} \\ \text { Panjang sebenar padang } & =6 \mathrm{~cm} \times 2000 \\ & =12000 \mathrm{~cm} \\ & =120 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} \frac{1}{2000} & =\frac{3 \mathrm{~cm}}{\text { Lebar sebenar padang }} \\ \text { Lebar sebenar padang } & =3 \mathrm{~cm} \times 2000 \\ & =6000 \mathrm{~cm} \\ & =60 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} \text { Luas sebenar padang } & =120 \mathrm{~m} \times 60 \mathrm{~m} \\ & =7200 \mathrm{~m}^2 \end{aligned} $$
(b)
Guna kaedah kadaran:
$$ \begin{aligned} & \frac{\text { Masa utk memotong semua rumput }}{\text { Rumput dalam meter persegi }}=\frac{\text { Masa utk memotong } 400 \mathrm{~m}^2 \text { rumput }}{\text { Rumput dalam meter persegi }} \\ & \begin{aligned} & \frac{\text { Masa untuk memotong semua rumput }}{7200 \mathrm{~m}^2}=\frac{8 \mathrm{~min}}{400 \mathrm{~m}^2} \\ & \begin{aligned} \text { Masa untuk memotong semua rumput } & =\frac{8 \mathrm{~min}}{400 \mathrm{~m}^2} \times 7200 \mathrm{~m}^2 \\ & =144 \mathrm{~min} \\ & =\frac{144 \mathrm{~min}}{60} \\ & =2.4 \text { jam } \\ & =2 \text { jam }+(0.4 \times 60 \mathrm{~min}) \\ & =2 \text { jam } 24 \mathrm{minit} \end{aligned} \end{aligned} . \begin{aligned} \end{aligned} \\ & \begin{aligned} \end{aligned} \\ & \end{aligned} $$

Rajah di atas menunjukkan lukisan berskala bagi sebuah padang yang berbentuk segi empat tepat.
(a) Jika skala yang digunakan ialah 1 : 2 000, hitung luas sebenar padang itu dalam meter persegi.
(b) Encik Dany memotong rumput di padang tersebut dengan kadar 400 meter persegi dalam masa 8 minit. Hitung tempoh masa, dalam jam dan minit, yang diperlukan oleh Encik Dany untuk memotong rumput keseluruhan padang tersebut.
Penyelesaian:
(a)
$$ \text { Skala }=\frac{\text { Sisi lukisan berskala }}{\text { Sisi objek yang sepadan }} $$
$$ \begin{aligned} \frac{1}{2000} & =\frac{6 \mathrm{~cm}}{\text { Panjang sebenar padang }} \\ \text { Panjang sebenar padang } & =6 \mathrm{~cm} \times 2000 \\ & =12000 \mathrm{~cm} \\ & =120 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} \frac{1}{2000} & =\frac{3 \mathrm{~cm}}{\text { Lebar sebenar padang }} \\ \text { Lebar sebenar padang } & =3 \mathrm{~cm} \times 2000 \\ & =6000 \mathrm{~cm} \\ & =60 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} \text { Luas sebenar padang } & =120 \mathrm{~m} \times 60 \mathrm{~m} \\ & =7200 \mathrm{~m}^2 \end{aligned} $$
(b)
Guna kaedah kadaran:
$$ \begin{aligned} & \frac{\text { Masa utk memotong semua rumput }}{\text { Rumput dalam meter persegi }}=\frac{\text { Masa utk memotong } 400 \mathrm{~m}^2 \text { rumput }}{\text { Rumput dalam meter persegi }} \\ & \begin{aligned} & \frac{\text { Masa untuk memotong semua rumput }}{7200 \mathrm{~m}^2}=\frac{8 \mathrm{~min}}{400 \mathrm{~m}^2} \\ & \begin{aligned} \text { Masa untuk memotong semua rumput } & =\frac{8 \mathrm{~min}}{400 \mathrm{~m}^2} \times 7200 \mathrm{~m}^2 \\ & =144 \mathrm{~min} \\ & =\frac{144 \mathrm{~min}}{60} \\ & =2.4 \text { jam } \\ & =2 \text { jam }+(0.4 \times 60 \mathrm{~min}) \\ & =2 \text { jam } 24 \mathrm{minit} \end{aligned} \end{aligned} . \begin{aligned} \end{aligned} \\ & \begin{aligned} \end{aligned} \\ & \end{aligned} $$