Soalan 1:
Tentukan sama ada setiap nombor yang berikut ialah kuasa dua sempurna atau bukan. Gunakan kaedah pemfaktoran perdana untuk menyokong jawapan anda.
(a) 216
(b) 1 000
(c) 1 024
Penyelesaian:
1. Pemfaktoran perdana suatu nombor boleh dilakukan dengan pembahagian berulang dengan nombor perdana.
2. Lakukan pembahagian berulang dengan nombor perdana terkecil.
3. Pembahagian diteruskan sehingga hasil bahaginya menjadi 1.
(a) 216
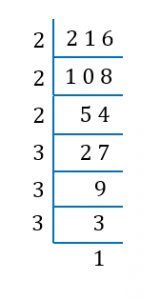
216 = (2 × 2 × 2) × (3 × 3 × 3)
= 23 × 33
Faktor perdana tidak boleh dikumpulkan dalam dua kumpulan yang sama.
Maka, 216 bukan kuasa dua sempurna.
(b) 1000
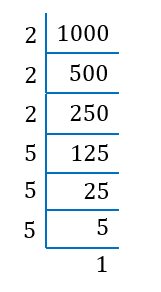
1000 = (2 × 2 × 2) × (5 × 5 × 5)
= 23 × 53
Faktor perdana tidak boleh dikumpulkan dalam dua kumpulan yang sama.
Maka, 1000 bukan kuasa dua sempurna.”
(c) 1024
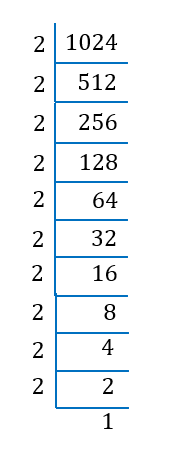
1024 = 25 × 25
Faktor perdana boleh dikumpulkan dalam dua kumpulan yang sama.
Maka, 1024 ialah kuasa dua sempurna.
Tentukan sama ada setiap nombor yang berikut ialah kuasa dua sempurna atau bukan. Gunakan kaedah pemfaktoran perdana untuk menyokong jawapan anda.
(a) 216
(b) 1 000
(c) 1 024
Penyelesaian:
1. Pemfaktoran perdana suatu nombor boleh dilakukan dengan pembahagian berulang dengan nombor perdana.
2. Lakukan pembahagian berulang dengan nombor perdana terkecil.
3. Pembahagian diteruskan sehingga hasil bahaginya menjadi 1.
(a) 216

216 = (2 × 2 × 2) × (3 × 3 × 3)
= 23 × 33
Faktor perdana tidak boleh dikumpulkan dalam dua kumpulan yang sama.
Maka, 216 bukan kuasa dua sempurna.
(b) 1000
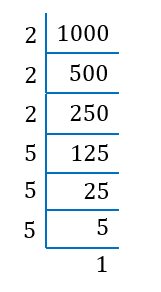
1000 = (2 × 2 × 2) × (5 × 5 × 5)
= 23 × 53
Faktor perdana tidak boleh dikumpulkan dalam dua kumpulan yang sama.
Maka, 1000 bukan kuasa dua sempurna.”
(c) 1024

1024 = 25 × 25
Faktor perdana boleh dikumpulkan dalam dua kumpulan yang sama.
Maka, 1024 ialah kuasa dua sempurna.
Soalan 2:
Pemfaktoran perdana bagi 100 ialah 2 × 2 × 5 × 5. Terangkan bagaimana anda mencari punca kuasa dua bagi 100 dengan menggunakan kaedah pemfaktoran perdana.
Penyelesaian:
100 = 2 × 2 × 5 × 5
= (2 × 5) × (2 × 5)
Faktor perdana boleh dikumpulkan dalam dua kumpulan yang sama.
Maka, 100 ialah kuasa dua sempurna.
$$ \begin{aligned} \sqrt{100} & =\sqrt{2 \times 5 \times 2 \times 5} \\ & =\sqrt{10 \times 10} \\ & =10 \end{aligned} $$
Pemfaktoran perdana bagi 100 ialah 2 × 2 × 5 × 5. Terangkan bagaimana anda mencari punca kuasa dua bagi 100 dengan menggunakan kaedah pemfaktoran perdana.
Penyelesaian:
100 = 2 × 2 × 5 × 5
= (2 × 5) × (2 × 5)
Faktor perdana boleh dikumpulkan dalam dua kumpulan yang sama.
Maka, 100 ialah kuasa dua sempurna.
$$ \begin{aligned} \sqrt{100} & =\sqrt{2 \times 5 \times 2 \times 5} \\ & =\sqrt{10 \times 10} \\ & =10 \end{aligned} $$
Soalan 3:
Salin dan lengkapkan setiap yang berikut berdasarkan hubungan kuasa dua dan punca kuasa dua.
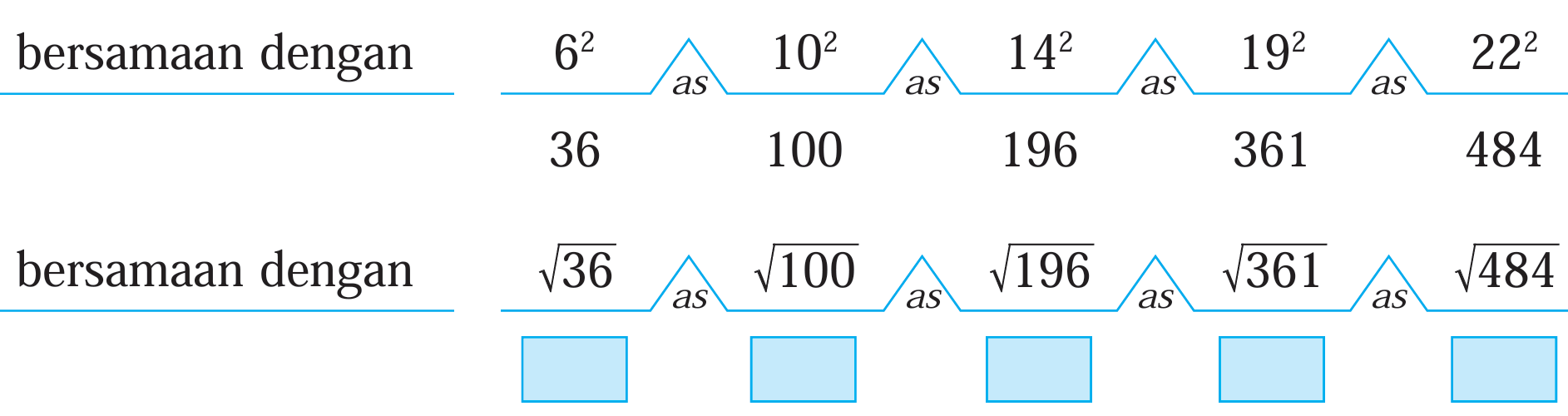
Penyelesaian:
$$ \begin{aligned} 6^2 & =36 \\ \sqrt{36} & =\sqrt{6 \times 6} \\ & =6 \end{aligned} $$
$$ \begin{aligned} 10^2 & =100 \\ \sqrt{100} & =\sqrt{10 \times 10} \\ & =10 \end{aligned} $$
$$ \begin{aligned} 14^2 & =196 \\ \sqrt{196} & =\sqrt{14 \times 14} \\ & =14 \end{aligned} $$
$$ \begin{aligned} 19^2 & =361 \\ \sqrt{361} & =\sqrt{19 \times 19} \\ & =19 \end{aligned} $$
$$ \begin{aligned} 22^2 & =484 \\ \sqrt{484} & =\sqrt{22 \times 22} \\ & =22 \end{aligned} $$
Salin dan lengkapkan setiap yang berikut berdasarkan hubungan kuasa dua dan punca kuasa dua.

Penyelesaian:
$$ \begin{aligned} 6^2 & =36 \\ \sqrt{36} & =\sqrt{6 \times 6} \\ & =6 \end{aligned} $$
$$ \begin{aligned} 10^2 & =100 \\ \sqrt{100} & =\sqrt{10 \times 10} \\ & =10 \end{aligned} $$
$$ \begin{aligned} 14^2 & =196 \\ \sqrt{196} & =\sqrt{14 \times 14} \\ & =14 \end{aligned} $$
$$ \begin{aligned} 19^2 & =361 \\ \sqrt{361} & =\sqrt{19 \times 19} \\ & =19 \end{aligned} $$
$$ \begin{aligned} 22^2 & =484 \\ \sqrt{484} & =\sqrt{22 \times 22} \\ & =22 \end{aligned} $$