Soalan 6:
Tentukan bilangan sisi bagi poligon yang mempunyai hasil tambah sudut pedalaman
(a) 900°
(b) 1 080°
(c) 1 260°
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Hasil tambah sudut pedalaman suatu poligon }\\ &\begin{aligned} &=(n-2) \times 180^{\circ} \\ & 900^{\circ}=(n-2) \times 180^{\circ} \\ & n-2=\frac{900^{\circ}}{180^{\circ}} \\ & n-2=5 \\ & n=5+2 \\ & n=7 \text { sisi } \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Hasil tambah sudut pedalaman suatu poligon }\\ &\begin{aligned} & =(n-2) \times 180^{\circ} \\ & 1080^{\circ}=(n-2) \times 180^{\circ} \\ & n-2=\frac{1080^{\circ}}{180^{\circ}} \\ & n-2=6 \\ & n=6+2 \\ & n=8 \text { sisi } \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Hasil tambah sudut pedalaman suatu poligon }\\ &\begin{aligned} & =(n-2) \times 180^{\circ} \\ & 1260^{\circ}=(n-2) \times 180^{\circ} \\ & n-2=\frac{1260^{\circ}}{180^{\circ}} \\ & n-2=7 \\ & n=7+2 \\ & n=9 \text { sisi } \end{aligned} \end{aligned} $$
Tentukan bilangan sisi bagi poligon yang mempunyai hasil tambah sudut pedalaman
(a) 900°
(b) 1 080°
(c) 1 260°
Penyelesaian:
(a)
$$ \begin{aligned} &\text { Hasil tambah sudut pedalaman suatu poligon }\\ &\begin{aligned} &=(n-2) \times 180^{\circ} \\ & 900^{\circ}=(n-2) \times 180^{\circ} \\ & n-2=\frac{900^{\circ}}{180^{\circ}} \\ & n-2=5 \\ & n=5+2 \\ & n=7 \text { sisi } \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Hasil tambah sudut pedalaman suatu poligon }\\ &\begin{aligned} & =(n-2) \times 180^{\circ} \\ & 1080^{\circ}=(n-2) \times 180^{\circ} \\ & n-2=\frac{1080^{\circ}}{180^{\circ}} \\ & n-2=6 \\ & n=6+2 \\ & n=8 \text { sisi } \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Hasil tambah sudut pedalaman suatu poligon }\\ &\begin{aligned} & =(n-2) \times 180^{\circ} \\ & 1260^{\circ}=(n-2) \times 180^{\circ} \\ & n-2=\frac{1260^{\circ}}{180^{\circ}} \\ & n-2=7 \\ & n=7+2 \\ & n=9 \text { sisi } \end{aligned} \end{aligned} $$
Soalan 7:
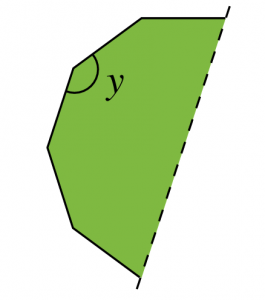
Zaidi mempunyai sebuah kebun sayur berbentuk poligon sekata. Garis putus-putus dalam rajah di bawah merupakan paksi simetri kebun beliau.
(a) Apakah bentuk sebenar kebun sayur Zaidi?
(b) Hitung nilai y.
Penyelesaian:
(a)
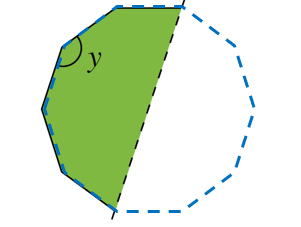
(b)
$$ \begin{aligned} &\text { Sudut pedalaman poligon sekata }\\ &\begin{aligned} & =\frac{(n-2) \times 180^{\circ}}{n} \\ & =\frac{(10-2) \times 180^{\circ}}{10} \\ & =\frac{8 \times 180^{\circ}}{10} \\ & =\frac{1440^{\circ}}{10} \\ & =144^{\circ} \end{aligned} \end{aligned} $$

Zaidi mempunyai sebuah kebun sayur berbentuk poligon sekata. Garis putus-putus dalam rajah di bawah merupakan paksi simetri kebun beliau.
(a) Apakah bentuk sebenar kebun sayur Zaidi?
(b) Hitung nilai y.
Penyelesaian:
(a)

Bentuk Dekagon (10 sisi) adalah bentuk sebenar kebun sayur Zaidi.
(b)
$$ \begin{aligned} &\text { Sudut pedalaman poligon sekata }\\ &\begin{aligned} & =\frac{(n-2) \times 180^{\circ}}{n} \\ & =\frac{(10-2) \times 180^{\circ}}{10} \\ & =\frac{8 \times 180^{\circ}}{10} \\ & =\frac{1440^{\circ}}{10} \\ & =144^{\circ} \end{aligned} \end{aligned} $$
Soalan 8:
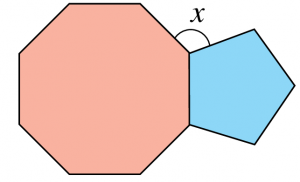
Rajah menunjukkan dua buah kolam renang di sebuah pusat sukan berbentuk oktagon dan pentagon sekata. Apakah nilai sudut x?
Penyelesaian:
$$ \text { Sudut pedalaman poligon sekata }=\frac{(n-2) \times 180^{\circ}}{n} $$
$$ \begin{aligned} \text { Sudut pedalaman oktagon sekata } & =\frac{(8-2) \times 180^{\circ}}{8} \\ & =\frac{6 \times 180^{\circ}}{8} \\ & =\frac{1080^{\circ}}{8} \\ & =135^{\circ} \end{aligned} $$
$$ \begin{aligned} \text { Sudut pedalaman pentagon sekata } & =\frac{(5-2) \times 180^{\circ}}{5} \\ & =\frac{3 \times 180^{\circ}}{5} \\ & =108^{\circ} \end{aligned} $$
$$ \begin{aligned} x+135^{\circ}+108^{\circ} & =360^{\circ} \\ x+243^{\circ} & =360^{\circ} \\ x & =360^{\circ}-243^{\circ} \\ x & =117^{\circ} \end{aligned} $$
Rajah menunjukkan dua buah kolam renang di sebuah pusat sukan berbentuk oktagon dan pentagon sekata. Apakah nilai sudut x?

Penyelesaian:
$$ \text { Sudut pedalaman poligon sekata }=\frac{(n-2) \times 180^{\circ}}{n} $$
$$ \begin{aligned} \text { Sudut pedalaman oktagon sekata } & =\frac{(8-2) \times 180^{\circ}}{8} \\ & =\frac{6 \times 180^{\circ}}{8} \\ & =\frac{1080^{\circ}}{8} \\ & =135^{\circ} \end{aligned} $$
$$ \begin{aligned} \text { Sudut pedalaman pentagon sekata } & =\frac{(5-2) \times 180^{\circ}}{5} \\ & =\frac{3 \times 180^{\circ}}{5} \\ & =108^{\circ} \end{aligned} $$
$$ \begin{aligned} x+135^{\circ}+108^{\circ} & =360^{\circ} \\ x+243^{\circ} & =360^{\circ} \\ x & =360^{\circ}-243^{\circ} \\ x & =117^{\circ} \end{aligned} $$