Soalan 4:
Seorang pengurus cawangan kedai makanan segera dibayar gaji 3 kali ganda berbanding dengan gaji pekerja sambilan, RMx sehari. Masa bekerja untuk pekerja sambilan ialah separuh dari masa bekerja pengurus itu, y dalam tempoh sebulan. Jika mereka bekerja 26 hari dalam sebulan, tulis rumus perbezaan gaji, RMz antara kedua-dua pekerja tersebut dalam sebutan x dan y.
Penyelesaian:
Katakan x = gaji sejam bagi seorang pekerja sambilan
3x = gaji sejam bagi seorang pengurus
y = Masa bekerja sehari untuk pengurus
y/2 = Masa bekerja sehari untuk pekerja sambilan
$$ \begin{aligned} & \text { Gaji bulanan bagi pengurus } \\ & =\text { Gaji sejam } \times \text { kerja sehari }(j a m) \times \\ & \quad \text { masa bekerja dlm tempoh sebulan } \\ & =(3 x)(y)(26) \\ & =78 x y \end{aligned} $$
$$ \begin{aligned} &\text { Gaji bulanan bagi pekerja sambilan }\\ &\begin{aligned} & =(x)\left(\frac{y}{2}\right)(26) \\ & =13 x y \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Perbezaan gaji, RMz antara pengurus dan pekerja sambilan }\\ &\begin{aligned} & z=78 x y-13 x y \\ & z=65 x y \end{aligned} \end{aligned} $$
Seorang pengurus cawangan kedai makanan segera dibayar gaji 3 kali ganda berbanding dengan gaji pekerja sambilan, RMx sehari. Masa bekerja untuk pekerja sambilan ialah separuh dari masa bekerja pengurus itu, y dalam tempoh sebulan. Jika mereka bekerja 26 hari dalam sebulan, tulis rumus perbezaan gaji, RMz antara kedua-dua pekerja tersebut dalam sebutan x dan y.
Penyelesaian:
Katakan x = gaji sejam bagi seorang pekerja sambilan
3x = gaji sejam bagi seorang pengurus
y = Masa bekerja sehari untuk pengurus
y/2 = Masa bekerja sehari untuk pekerja sambilan
$$ \begin{aligned} & \text { Gaji bulanan bagi pengurus } \\ & =\text { Gaji sejam } \times \text { kerja sehari }(j a m) \times \\ & \quad \text { masa bekerja dlm tempoh sebulan } \\ & =(3 x)(y)(26) \\ & =78 x y \end{aligned} $$
$$ \begin{aligned} &\text { Gaji bulanan bagi pekerja sambilan }\\ &\begin{aligned} & =(x)\left(\frac{y}{2}\right)(26) \\ & =13 x y \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Perbezaan gaji, RMz antara pengurus dan pekerja sambilan }\\ &\begin{aligned} & z=78 x y-13 x y \\ & z=65 x y \end{aligned} \end{aligned} $$
Soalan 5:
Julia mengambil 40 saat untuk berjalan sejauh 50 meter. Bantu Julia menulis rumus mengira tempoh perjalanan, t dalam minit, dari rumahnya ke sekolah yang berjarak s kilometer.
Penyelesaian:
Diberi laju bagi Julia adalah 40 saat untuk berjalan 50 m
$$ \begin{aligned} \text { Laju } & =\frac{\text { Jarak }}{\text { Masa }} \\ & =\frac{\frac{50}{1000} \mathrm{~km}}{\frac{40}{60} \mathrm{~min}} \\ & =\frac{50}{1000} \times \frac{60}{40} \\ & =\frac{3}{40} \mathrm{~km} / \mathrm{min} \end{aligned} $$
$$ \begin{aligned} &\text { Tempoh perjalanan bagi Julia untuk berjalan } s \mathrm{~km} \text {, }\\ &\begin{aligned} & t=\frac{J a r a k(\mathrm{~km})}{\mathrm{Laju}(\mathrm{~km} / \mathrm{min})} \\ & t=\frac{s}{\frac{3}{40}} \\ & t=s \times \frac{40}{3} \\ & t=13 \frac{1}{3} \mathrm{~s} \mathrm{~min} \end{aligned} \end{aligned} $$
Julia mengambil 40 saat untuk berjalan sejauh 50 meter. Bantu Julia menulis rumus mengira tempoh perjalanan, t dalam minit, dari rumahnya ke sekolah yang berjarak s kilometer.
Penyelesaian:
Diberi laju bagi Julia adalah 40 saat untuk berjalan 50 m
$$ \begin{aligned} \text { Laju } & =\frac{\text { Jarak }}{\text { Masa }} \\ & =\frac{\frac{50}{1000} \mathrm{~km}}{\frac{40}{60} \mathrm{~min}} \\ & =\frac{50}{1000} \times \frac{60}{40} \\ & =\frac{3}{40} \mathrm{~km} / \mathrm{min} \end{aligned} $$
$$ \begin{aligned} &\text { Tempoh perjalanan bagi Julia untuk berjalan } s \mathrm{~km} \text {, }\\ &\begin{aligned} & t=\frac{J a r a k(\mathrm{~km})}{\mathrm{Laju}(\mathrm{~km} / \mathrm{min})} \\ & t=\frac{s}{\frac{3}{40}} \\ & t=s \times \frac{40}{3} \\ & t=13 \frac{1}{3} \mathrm{~s} \mathrm{~min} \end{aligned} \end{aligned} $$
Soalan 6:
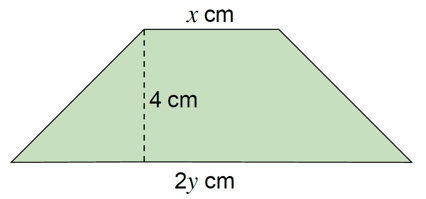
Luas trapezium di bawah ialah 36 cm2. Jika x + y = 11 cm, hitung nilai x dan y.
Penyelesaian:
$$ \begin{aligned} &\text { Luas trapezium ialah } 36 \mathrm{~cm}^2\\ &\begin{aligned} \frac{1}{2}(x+2 y)(4) & =36 \\ x+2 y & =36 \times \frac{2}{4} \\ x+2 y & =18 \\ x & =18-2 y \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Diberi } x+y & =11 \\ x & =11-y \ldots(2) \end{aligned} $$
$$ \begin{aligned} (1)-(2), & 0=7-y \\ y & =7 \end{aligned} $$
$$ \begin{aligned} & \text { Gantikan } y=7 \text { ke dalam (2), } \\ & x=11-7 \\ & x=4 \end{aligned} $$
Luas trapezium di bawah ialah 36 cm2. Jika x + y = 11 cm, hitung nilai x dan y.

Penyelesaian:
$$ \begin{aligned} &\text { Luas trapezium ialah } 36 \mathrm{~cm}^2\\ &\begin{aligned} \frac{1}{2}(x+2 y)(4) & =36 \\ x+2 y & =36 \times \frac{2}{4} \\ x+2 y & =18 \\ x & =18-2 y \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Diberi } x+y & =11 \\ x & =11-y \ldots(2) \end{aligned} $$
$$ \begin{aligned} (1)-(2), & 0=7-y \\ y & =7 \end{aligned} $$
$$ \begin{aligned} & \text { Gantikan } y=7 \text { ke dalam (2), } \\ & x=11-7 \\ & x=4 \end{aligned} $$