Soalan 3:
Permudah setiap ungkapan berikut.
$$ \text { (a) } \frac{a+2}{4 v}+\frac{a-b}{2 v} $$
$$ \text { (b) } \frac{3 e}{5 a b}-\frac{5 d}{4 c} $$
$$ \text { (c) } \frac{4}{f^2 g}-\frac{3}{5 f g} $$
$$ \text { (d) } \frac{n+2}{m^2}+\frac{n}{m p} $$
$$ \text { (e) } \frac{5 x}{8 y z}+\frac{y-1}{12 x z} $$
$$ \text { (f) } \frac{r s}{4 y}+\frac{2-r}{18 y z} $$
Penyelesaian:
(a)
$$ \begin{aligned} & \frac{a+2}{4 v}+\frac{a-b}{2 v} \\ & =\frac{a+2}{4 v}+\frac{(a-b) \times 2}{2 v \times 2} \\ & =\frac{a+2}{4 v}+\frac{2(a-b)}{4 v} \\ & =\frac{a+2+2(a-b)}{4 v} \\ & =\frac{a+2+2 a-2 b}{4 v} \\ & =\frac{3 a-2 b+2}{4 v} \end{aligned} $$
(b)
$$ \begin{aligned} & \frac{3 e}{5 a b}-\frac{5 d}{4 c} \\ & =\frac{3 e \times 4 c}{5 a b \times 4 c}-\frac{5 d \times 5 a b}{4 c \times 5 a b} \\ & =\frac{12 c e}{20 a b c}-\frac{25 a b d}{20 a b c} \\ & =\frac{12 c e-25 a b d}{20 a b c} \end{aligned} $$
(c)
$$ \begin{aligned} & \frac{4}{f^2 g}-\frac{3}{5 f g} \\ = & \frac{4 \times 5}{f^2 g \times 5}-\frac{3 \times f}{5 f g \times f} \\ = & \frac{20}{5 f^2 g}-\frac{3 f}{5 f^2 g} \\ = & \frac{20-3 f}{5 f^2 g} \end{aligned} $$
 $$
\begin{aligned}
\text { GSTK } & =(f)(g)(f)(5) \\
& =5 f^2 g
\end{aligned}
$$
$$
\begin{aligned}
\text { GSTK } & =(f)(g)(f)(5) \\
& =5 f^2 g
\end{aligned}
$$
(d)
$$ \begin{aligned} & \frac{n+2}{m^2}+\frac{n}{m p} \\ = & \frac{(n+2) \times p}{m^2 \times p}+\frac{n \times m}{m p \times m} \\ = & \frac{n p+2 p}{m^2 p}+\frac{m n}{m^2 p} \\ = & \frac{n p+2 p+m n}{m^2 p} \end{aligned} $$
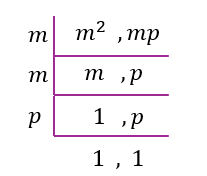 $$
\begin{aligned}
\mathrm{GSTK} & =(m)(m)(p) \\
& =m^2 p
\end{aligned}
$$
$$
\begin{aligned}
\mathrm{GSTK} & =(m)(m)(p) \\
& =m^2 p
\end{aligned}
$$
(e)
$$ \begin{aligned} & \frac{5 x}{8 y z}+\frac{y-1}{12 x z} \\ = & \frac{5 x \times 3 x}{8 y z \times 3 x}+\frac{(y-1) \times 2 y}{12 x z \times 2 y} \\ = & \frac{15 x^2}{24 x y z}+\frac{2 y^2-2 y}{24 x y z} \\ = & \frac{15 x^2+2 y^2-2 y}{24 x y z} \end{aligned} $$
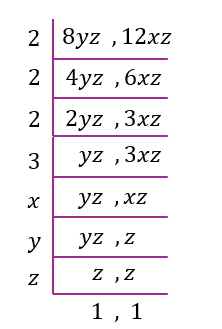 $$
\begin{aligned}
\text { GSTK } & =(2)(2)(2)(3)(x)(y)(z) \\
& =24 x y z
\end{aligned}
$$
$$
\begin{aligned}
\text { GSTK } & =(2)(2)(2)(3)(x)(y)(z) \\
& =24 x y z
\end{aligned}
$$
(f)
$$ \begin{aligned} & \frac{r s}{4 y}+\frac{2-r}{18 y z} \\ = & \frac{r s \times 9 z}{4 y \times 9 z}+\frac{(2-r) \times 2}{18 y z \times 2} \\ = & \frac{9 r s z}{36 y z}+\frac{4-2 r}{36 y z} \\ = & \frac{9 r s z+4-2 r}{36 y z} \end{aligned} $$
 $$
\begin{aligned}
\operatorname{GSTK} & =(2)(2)(3)(3)(y)(z) \\
& =36 y z
\end{aligned}
$$
$$
\begin{aligned}
\operatorname{GSTK} & =(2)(2)(3)(3)(y)(z) \\
& =36 y z
\end{aligned}
$$
Permudah setiap ungkapan berikut.
$$ \text { (a) } \frac{a+2}{4 v}+\frac{a-b}{2 v} $$
$$ \text { (b) } \frac{3 e}{5 a b}-\frac{5 d}{4 c} $$
$$ \text { (c) } \frac{4}{f^2 g}-\frac{3}{5 f g} $$
$$ \text { (d) } \frac{n+2}{m^2}+\frac{n}{m p} $$
$$ \text { (e) } \frac{5 x}{8 y z}+\frac{y-1}{12 x z} $$
$$ \text { (f) } \frac{r s}{4 y}+\frac{2-r}{18 y z} $$
Penyelesaian:
(a)
$$ \begin{aligned} & \frac{a+2}{4 v}+\frac{a-b}{2 v} \\ & =\frac{a+2}{4 v}+\frac{(a-b) \times 2}{2 v \times 2} \\ & =\frac{a+2}{4 v}+\frac{2(a-b)}{4 v} \\ & =\frac{a+2+2(a-b)}{4 v} \\ & =\frac{a+2+2 a-2 b}{4 v} \\ & =\frac{3 a-2 b+2}{4 v} \end{aligned} $$
(b)
$$ \begin{aligned} & \frac{3 e}{5 a b}-\frac{5 d}{4 c} \\ & =\frac{3 e \times 4 c}{5 a b \times 4 c}-\frac{5 d \times 5 a b}{4 c \times 5 a b} \\ & =\frac{12 c e}{20 a b c}-\frac{25 a b d}{20 a b c} \\ & =\frac{12 c e-25 a b d}{20 a b c} \end{aligned} $$
(c)
$$ \begin{aligned} & \frac{4}{f^2 g}-\frac{3}{5 f g} \\ = & \frac{4 \times 5}{f^2 g \times 5}-\frac{3 \times f}{5 f g \times f} \\ = & \frac{20}{5 f^2 g}-\frac{3 f}{5 f^2 g} \\ = & \frac{20-3 f}{5 f^2 g} \end{aligned} $$
 $$
\begin{aligned}
\text { GSTK } & =(f)(g)(f)(5) \\
& =5 f^2 g
\end{aligned}
$$
$$
\begin{aligned}
\text { GSTK } & =(f)(g)(f)(5) \\
& =5 f^2 g
\end{aligned}
$$(d)
$$ \begin{aligned} & \frac{n+2}{m^2}+\frac{n}{m p} \\ = & \frac{(n+2) \times p}{m^2 \times p}+\frac{n \times m}{m p \times m} \\ = & \frac{n p+2 p}{m^2 p}+\frac{m n}{m^2 p} \\ = & \frac{n p+2 p+m n}{m^2 p} \end{aligned} $$
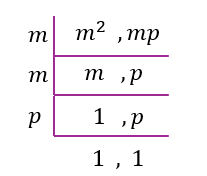 $$
\begin{aligned}
\mathrm{GSTK} & =(m)(m)(p) \\
& =m^2 p
\end{aligned}
$$
$$
\begin{aligned}
\mathrm{GSTK} & =(m)(m)(p) \\
& =m^2 p
\end{aligned}
$$(e)
$$ \begin{aligned} & \frac{5 x}{8 y z}+\frac{y-1}{12 x z} \\ = & \frac{5 x \times 3 x}{8 y z \times 3 x}+\frac{(y-1) \times 2 y}{12 x z \times 2 y} \\ = & \frac{15 x^2}{24 x y z}+\frac{2 y^2-2 y}{24 x y z} \\ = & \frac{15 x^2+2 y^2-2 y}{24 x y z} \end{aligned} $$
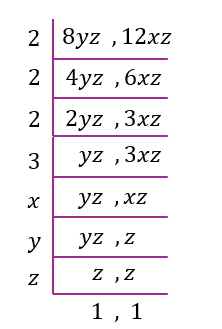 $$
\begin{aligned}
\text { GSTK } & =(2)(2)(2)(3)(x)(y)(z) \\
& =24 x y z
\end{aligned}
$$
$$
\begin{aligned}
\text { GSTK } & =(2)(2)(2)(3)(x)(y)(z) \\
& =24 x y z
\end{aligned}
$$(f)
$$ \begin{aligned} & \frac{r s}{4 y}+\frac{2-r}{18 y z} \\ = & \frac{r s \times 9 z}{4 y \times 9 z}+\frac{(2-r) \times 2}{18 y z \times 2} \\ = & \frac{9 r s z}{36 y z}+\frac{4-2 r}{36 y z} \\ = & \frac{9 r s z+4-2 r}{36 y z} \end{aligned} $$
 $$
\begin{aligned}
\operatorname{GSTK} & =(2)(2)(3)(3)(y)(z) \\
& =36 y z
\end{aligned}
$$
$$
\begin{aligned}
\operatorname{GSTK} & =(2)(2)(3)(3)(y)(z) \\
& =36 y z
\end{aligned}
$$Soalan 4:
Nenek mempunyai sekeping coklat berukuran (k2 – 16) cm panjang dan dia ingin membahagikannya kepada cucunya seramai (k – 4) orang. Berapakah ukuran panjang coklat yang akan diterima oleh setiap cucunya?
Penyelesaian:
$$ \begin{aligned} &\text { Ukuran panjang coklat yang akan diterima oleh setiap cucu }\\ &\begin{aligned} & =\left(k^2-16\right) \div(k-4) \\ & =\frac{k^2-16}{k-4} \\ & =\frac{k^2-4^2}{k-4} \\ & =\frac{(k+4)(k-4)}{k-4} \\ & =(k+4) \mathrm{cm} \end{aligned} \end{aligned} $$
Nenek mempunyai sekeping coklat berukuran (k2 – 16) cm panjang dan dia ingin membahagikannya kepada cucunya seramai (k – 4) orang. Berapakah ukuran panjang coklat yang akan diterima oleh setiap cucunya?
Penyelesaian:
$$ \begin{aligned} &\text { Ukuran panjang coklat yang akan diterima oleh setiap cucu }\\ &\begin{aligned} & =\left(k^2-16\right) \div(k-4) \\ & =\frac{k^2-16}{k-4} \\ & =\frac{k^2-4^2}{k-4} \\ & =\frac{(k+4)(k-4)}{k-4} \\ & =(k+4) \mathrm{cm} \end{aligned} \end{aligned} $$