Soalan 10:
Diberi jarak mencancang dari titik V yang terletak di utara titik W ialah 4 unit. Tentukan koordinat W jika koordinat V ialah
(a) (4, –3)
(b) (2, −5)
(c) (5, –2)
(d) (0, –4)
Penyelesaian:
Bagi jarak mencancang, koordinat x adalah sama.
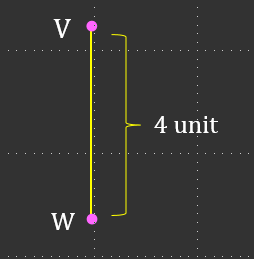
(a)
Bagi titik V (4, –3)
– 3 – y = 4
– y = 4 + 3
– y = 7
y = – 7
Maka, koordinat W = (4, -7)
(b)
Bagi titik V (2, –5)
– 5 – y = 4
– y = 4 + 5
– y = 9
y = – 9
Maka, koordinat W = (2, -9)
(c)
Bagi titik V (5, –2)
– 2 – y = 4
– y = 4 + 2
– y = 6
y = – 6
Maka, koordinat W = (5, -6)
(d)
Bagi titik V (0, –4)
– 4 – y = 4
– y = 4 + 4
– y = 8
y = – 8
Maka, koordinat W = (0, -8)
Diberi jarak mencancang dari titik V yang terletak di utara titik W ialah 4 unit. Tentukan koordinat W jika koordinat V ialah
(a) (4, –3)
(b) (2, −5)
(c) (5, –2)
(d) (0, –4)
Penyelesaian:
Bagi jarak mencancang, koordinat x adalah sama.

(a)
Bagi titik V (4, –3)
– 3 – y = 4
– y = 4 + 3
– y = 7
y = – 7
Maka, koordinat W = (4, -7)
(b)
Bagi titik V (2, –5)
– 5 – y = 4
– y = 4 + 5
– y = 9
y = – 9
Maka, koordinat W = (2, -9)
(c)
Bagi titik V (5, –2)
– 2 – y = 4
– y = 4 + 2
– y = 6
y = – 6
Maka, koordinat W = (5, -6)
(d)
Bagi titik V (0, –4)
– 4 – y = 4
– y = 4 + 4
– y = 8
y = – 8
Maka, koordinat W = (0, -8)
Soalan 11:
Berdasarkan rajah di bawah, hitung perimeter ABCD.
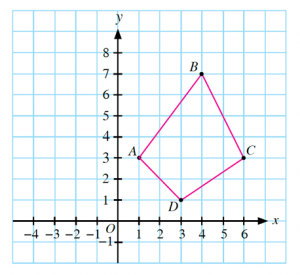
Penyelesaian:
Dengan menggunakan teorem Pythagoras,
\(\begin{aligned} A B^2 & =3^2+4^2 \\ A B^2 & =9+16 \\ A B & =\sqrt{25} \\ A B & =5 \text { unit }\end{aligned}\)
\(\begin{aligned} B C^2 & =2^2+4^2 \\ B C^2 & =4+16 \\ B C & =\sqrt{20} \\ B C & =4.47 \text { unit }\end{aligned}\)
\(\begin{aligned} C D^2 & =3^2+2^2 \\ C D^2 & =9+4 \\ C D & =\sqrt{13} \\ C D & =3.61 \text { unit }\end{aligned}\)
\(\begin{aligned} A D^2 & =2^2+2^2 \\ A D^2 & =4+4 \\ A D & =\sqrt{8} \\ A D & =2.83 \text { unit }\end{aligned}\)
Berdasarkan rajah di bawah, hitung perimeter ABCD.

Penyelesaian:
Dengan menggunakan teorem Pythagoras,
\(\begin{aligned} A B^2 & =3^2+4^2 \\ A B^2 & =9+16 \\ A B & =\sqrt{25} \\ A B & =5 \text { unit }\end{aligned}\)
\(\begin{aligned} B C^2 & =2^2+4^2 \\ B C^2 & =4+16 \\ B C & =\sqrt{20} \\ B C & =4.47 \text { unit }\end{aligned}\)
\(\begin{aligned} C D^2 & =3^2+2^2 \\ C D^2 & =9+4 \\ C D & =\sqrt{13} \\ C D & =3.61 \text { unit }\end{aligned}\)
\(\begin{aligned} A D^2 & =2^2+2^2 \\ A D^2 & =4+4 \\ A D & =\sqrt{8} \\ A D & =2.83 \text { unit }\end{aligned}\)
Maka, perimeter ABCD ialah
5 + 4.47 + 3.61+2.83
= 15.91 unit
Soalan 12:
Segi tiga ABC mempunyai bucu A (–2, –1), B (–2, 5) dan C (1, –1). Hitung perimeter bagi segi tiga itu.
Penyelesaian:
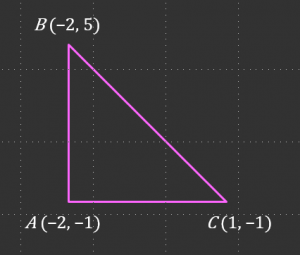
Segi tiga ABC mempunyai bucu A (–2, –1), B (–2, 5) dan C (1, –1). Hitung perimeter bagi segi tiga itu.
Penyelesaian:
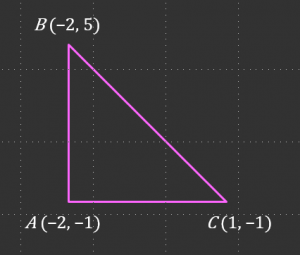
Jarak mencancang AB
= 5 – (-1)
= 5 + 1
= 6 unit
Jarak mengufuk AC
= 1 – (-2)
= 1 + 2
= 3 unit
\(\begin{aligned} B C^2 & =A B^2+A C^2 \\ B C^2 & =6^2+3^2 \\ B C^2 & =36+9 \\ B C & =\sqrt{45} \\ B C & =6.71 \text { unit }\end{aligned}\)
Maka, perimeter segi tiga ABC ialah
6 + 3 + 6.71
= 15.71 unit