9.1.1 Persamaan Garis Lurus
1. Jika nilai kecerunan, m, dan pintasan-y, c diberi, maka satu persamaan garis lurus
y = mx + c boleh dibentuk.
y = mx + c boleh dibentuk.
2. Jika suatu garis lurus diwakili oleh persamaan berbentuk y = mx + c, maka
(a) m ialah kecerunan,
(b) c ialah pintasan-y
(a) m ialah kecerunan,
(b) c ialah pintasan-y
Contoh 1:
Diberi persamaan bagi suatu garis lurus ialah y = 3 – 4x. Cari kecerunan dan pintasan-y
bagi garis ini.
bagi garis ini.
Penyelesaian:
y= 3 – 4x
y= – 4x + 3 ← (y = mx + c)
Oleh itu, kecerunan, m = – 4
pintasan-y, c = 3
3. Jika suatu persamaan garis lurus ditulis dalam bentuk ax + by + c = 0, maka tukarnya
kepada bentuk y = mx+ c untuk mencari nilai kecerunan dan pintasan-y.
kepada bentuk y = mx+ c untuk mencari nilai kecerunan dan pintasan-y.
Contoh 2:
Diberi persamaan bagi suatu garis lurus ialah 4x + 6y – 3 = 0. Cari kecerunan dan pintasan-y
bagi garis ini.
bagi garis ini.
Penyelesaian:
4x + 6y – 3 = 0
6y = –4x + 3
9.1.2 Persamaan Garis Lurus (Contoh Soalan)
Soalan 1:
Diberi persamaan bagi suatu garis lurus ialah 4x + 6y – 3 = 0. Apakah kecerunan garis lurus ini?
Penyelesaian:
Soalan 2:
Diberi persamaan bagi suatu garis lurus ialah y = – 7x + 3. Cari pintasan-y bagi garis ini.
Penyelesaian:
y= mx + c, c ialah pintasan- y garis lurus.
Oleh itu, bagi garis lurus y = – 7x + 3,
Pintasan-y ialah 3
Soalan 3:
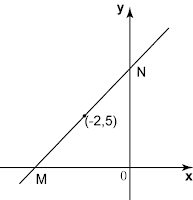

Cari persamaan bagi garis lurus MN jika kecerunannya ialah 3.
Penyelesaian:
Diberi m = 3
Gantikan nilai m = 3 dan (–2, 5) ke dalam y = mx + c.
5 = 3 (–2) + c
5 = –6 + c
c = 11
Oleh itu, persamaan bagi garis lurus MN ialah y = 3x + 11.