Soalan 4:
Rajah di bawah terdiri daripada dua buah segi tiga bersudut tegak.

Tentukan nilai kos xo.
Penyelesaian:
Soalan 5:
Rajah di bawah menunjukkan dua buah segi tiga bersudut tegak, ABE dan DBC.
ABC dan EBD ialah garis lurus.
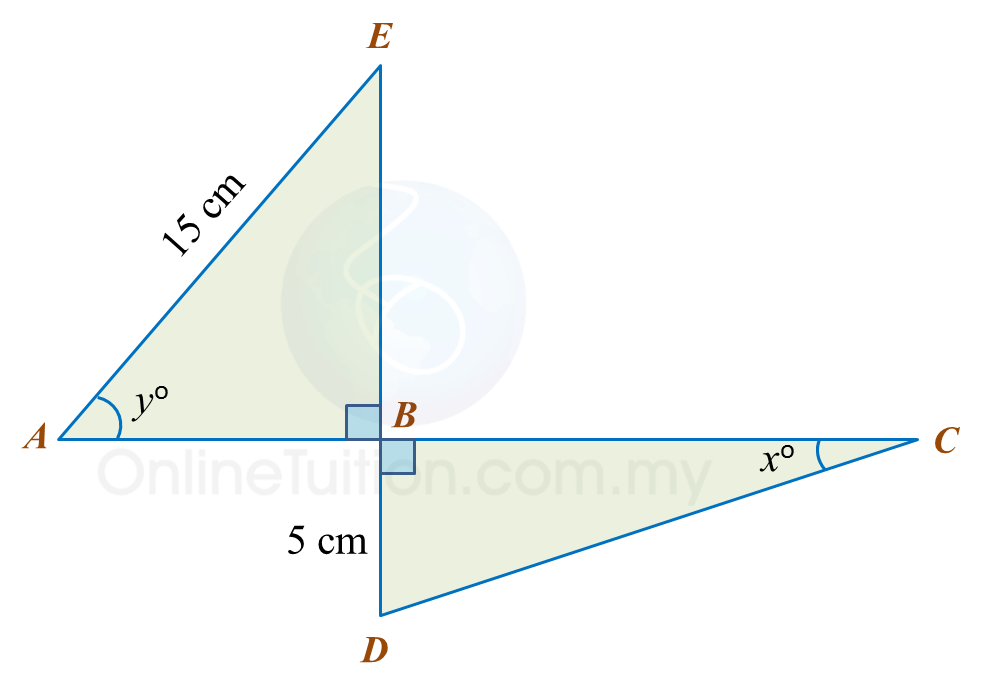
Rajah di bawah menunjukkan dua buah segi tiga bersudut tegak, ABE dan DBC.
ABC dan EBD ialah garis lurus.

Diberi bahawa
(a) Cari nilai bagi tan xo.
(b) Hitung panjang, dalam cm, bagi ABC.
(a) Cari nilai bagi tan xo.
(b) Hitung panjang, dalam cm, bagi ABC.
Penyelesaian:
(a)
(b)
Soalan 6:
Dalam rajah di bawah, ABE dan DBC ialah segi tiga bersudut tegak. ABC dan DEB ialah garis lurus.
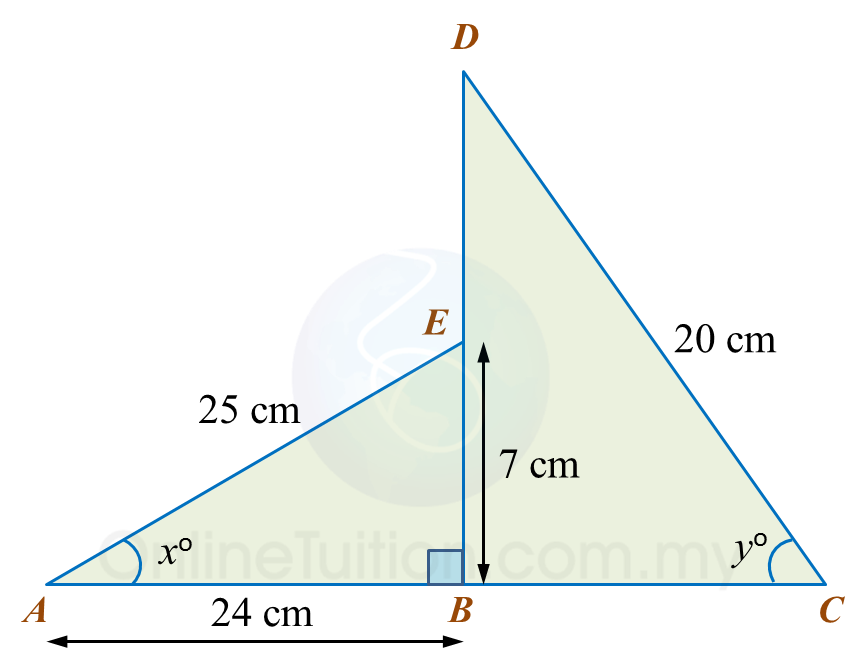
(a) Cari nilai bagi tan xo.
(b) Hitung panjang, dalam cm, DE.
Penyelesaian:
Dalam rajah di bawah, ABE dan DBC ialah segi tiga bersudut tegak. ABC dan DEB ialah garis lurus.

(a) Cari nilai bagi tan xo.
(b) Hitung panjang, dalam cm, DE.
Penyelesaian: