10.2.4 Perimeter dan Luas, Praktis Berformat PT3

Soalan 9:
Dalam rajah di bawah, ADB ialah sebuah segi tiga bersudut tegak dan DBFE ialah sebuah segi empat sama. C ialah titik tengah bagi DB dan CH = CD.
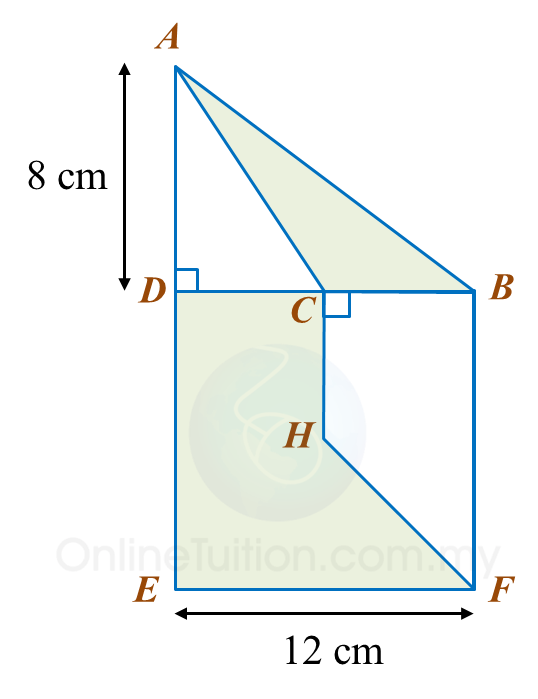Hitung luas, dalam cm², kawasan yang berlorek.

Penyelesaian:
$\begin{array}{l}\text{Luas }△ABC\\ =\frac{1}{2}\times 6\times 8\\ =24{\text{ cm}}^2\\ \\ \text{Luas trapezium }BCHF\\ =\frac{1}{2}\times \left(12+6\right)\times 6\\ =54{\text{ cm}}^2\\ \\ \text{Luas }CDEFH\\ =\left(12\times 12\right)-54\\ =144-54\\ =90{\text{ cm}}^2\\ \\ \text{Luas kawasan berlorek}\\ =24+90\\ =114{\text{ cm}}^2\end{array}$

Soalan 10:
Rajah di bawah menunjukkan segi empat tepat ACDE.

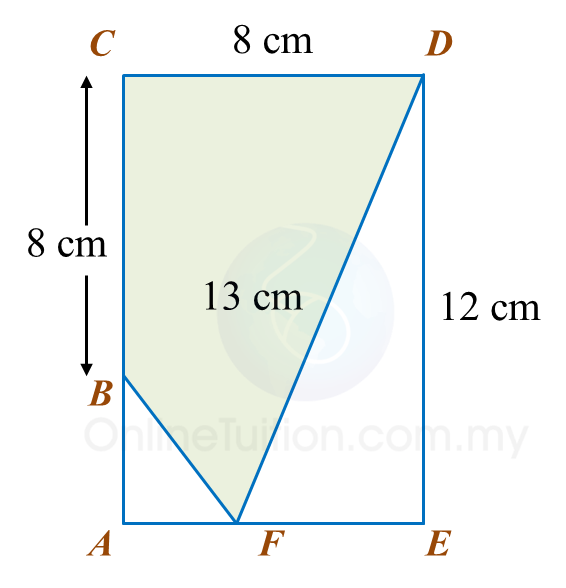
Hitung luas, dalam cm², kawasan yang berlorek.

Penyelesaian:
$\begin{array}{l}\text{Mengguna theorem Pythagoras (Rujuk Tingkatan 2 Bab 6)}\\ F{E}^2=D{F}^2-D{E}^2\\ ={13}^2-{12}^2\\ =169-144\\ =25\\ FE=\sqrt{25}=5\text{ cm}\\ \\ AF=8-5=3\text{ cm}\\ AB=12-8=4\text{ cm}\\ \\ \text{Luas segi empat tepat }ACDE\\ =8\times 12\\ =96{\text{ cm}}^2\\ \\ \text{Luas }△ABF\\ =\frac{1}{2}\times 3\times 4\\ =6{\text{ cm}}^2\\ \\ \text{Luas }△DEF\\ =\frac{1}{2}\times 5\times 12\\ =30{\text{ cm}}^2\\ \\ \text{Luas kawasan berlorek}\\ =96-30-6\\ =60{\text{ cm}}^2\end{array}$