Soalan 3 (a):
(i) Rajah 3.1 menunjukkan satu kaedah untuk mencari factor sepunya terbesar (FSTB) dan gandaan sepunya terkecil (GSTK) bagi 12 dan 32.
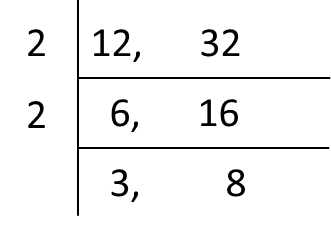Padankan jawapan yang betul.
Jawapan:
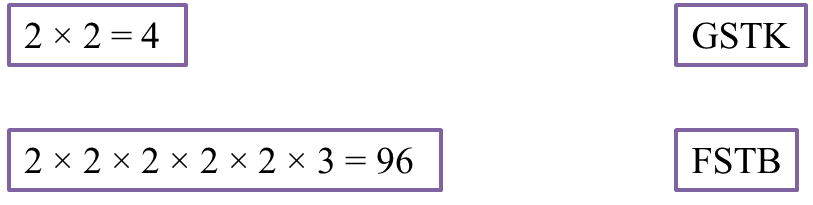
(ii) Beza antara dua nombor perdana ialah 9.
Tulis dua nombor perdana itu di ruang jawapan.
Jawapan:
( ) – ( ) = 9
Penyelesaian:
(i)
(ii)
( 11 ) – ( 2 ) = 9
(i) Rajah 3.1 menunjukkan satu kaedah untuk mencari factor sepunya terbesar (FSTB) dan gandaan sepunya terkecil (GSTK) bagi 12 dan 32.
Padankan jawapan yang betul.Jawapan:
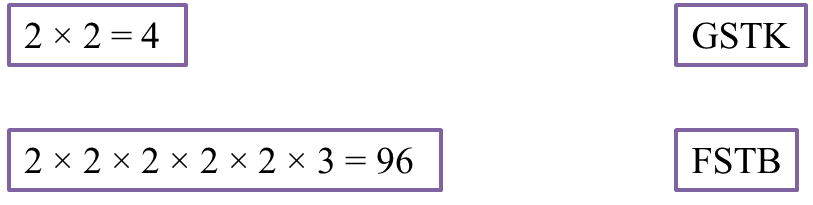
(ii) Beza antara dua nombor perdana ialah 9.
Tulis dua nombor perdana itu di ruang jawapan.
Jawapan:
( ) – ( ) = 9
Penyelesaian:
(i)
(ii)
( 11 ) – ( 2 ) = 9
Soalan 3 (b):
Rajah 3.2 dalam ruang jawapan menunjukkan garis lurus JK.
(i) Menggunakan pembaris dan jangka lukis sahaja, bina segi tiga JKL dengan KL = 8 cm dan ∠JKL = 135o. Anda boleh bermula dengan garis lurus JK yang disediakan pada ruang jawapan.
Jawapan:
(ii) Ukur ∠KJL dengan menggunakan protraktor.
Penyelesaian:
(i)
(ii)
∠KJL = 26o
Rajah 3.2 dalam ruang jawapan menunjukkan garis lurus JK.
(i) Menggunakan pembaris dan jangka lukis sahaja, bina segi tiga JKL dengan KL = 8 cm dan ∠JKL = 135o. Anda boleh bermula dengan garis lurus JK yang disediakan pada ruang jawapan.
Jawapan:
(ii) Ukur ∠KJL dengan menggunakan protraktor.
Penyelesaian:
(i)
(ii)
∠KJL = 26o
Soalan 3 (c):
Senaraikan semua nilai integer x yang memuaskan ketaksamaan linear berikut:
–1 ≤ 1 + 2x < 5
Penyelesaian:
–1 ≤ 1 + 2x < 5
–1 ≤ 1 + 2x dan 1 + 2x < 5
–2x ≤ 1 + 1 dan 2x < 5 – 1
–2x ≤ 2 dan 2x < 4
x ≥ –1 dan x < 2
x = –1, 0, 1, 2, … dan x = 1, 0, –1, –2 …
Maka x = –1, 0, 1.
Senaraikan semua nilai integer x yang memuaskan ketaksamaan linear berikut:
–1 ≤ 1 + 2x < 5
Penyelesaian:
–1 ≤ 1 + 2x < 5
–1 ≤ 1 + 2x dan 1 + 2x < 5
–2x ≤ 1 + 1 dan 2x < 5 – 1
–2x ≤ 2 dan 2x < 4
x ≥ –1 dan x < 2
x = –1, 0, 1, 2, … dan x = 1, 0, –1, –2 …
Maka x = –1, 0, 1.