Soalan 3:
Jika garis PQ selari dengan paksi-y dan mempunyai titik tengah, M(4, 0) dengan jarak bagi garis lurus MP ialah 3 unit, hitung
(a) koordinat P.
(b) koordinat Q.
(c) jarak PQ.
Penyelesaian:
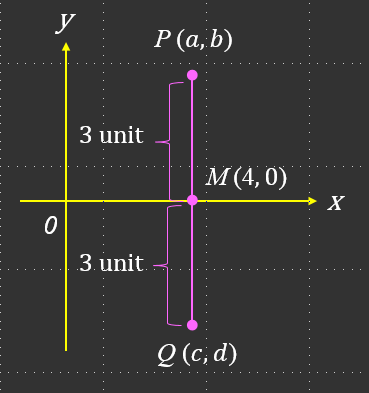
(a)
Koordinat x bagi titik P dan titik M adalah sama.
Titik P berada 3 unit di atas titik M.
∴ P (4, 3)
(b)
Koordinat x bagi titik Q dan titik M adalah sama juga.
Titik Q berada 3 unit di bawah titik M.
∴ Q (4, -3)
(c)
M ialah titik tengah bagi titik PQ, maka MP = MQ = 3 unit
Jarak PQ (Jarak menegak) = 3 + 3
= 6 unit
Jika garis PQ selari dengan paksi-y dan mempunyai titik tengah, M(4, 0) dengan jarak bagi garis lurus MP ialah 3 unit, hitung
(a) koordinat P.
(b) koordinat Q.
(c) jarak PQ.
Penyelesaian:

(a)
Koordinat x bagi titik P dan titik M adalah sama.
Titik P berada 3 unit di atas titik M.
∴ P (4, 3)
(b)
Koordinat x bagi titik Q dan titik M adalah sama juga.
Titik Q berada 3 unit di bawah titik M.
∴ Q (4, -3)
(c)
M ialah titik tengah bagi titik PQ, maka MP = MQ = 3 unit
Jarak PQ (Jarak menegak) = 3 + 3
= 6 unit
Soalan 4:
Jarak AB = KL, iaitu 8 unit dan masing-masing selari dengan paksi-x. Jika titik tengah bagi garis lurus AB ialah (0, 3) dan jarak titik tengah bagi garis lurus AB ke titik tengah bagi garis lurus KL ialah 2 unit ke bawah, hitung
(a) koordinat K dan L.
(b) koordinat titik tengah bagi garis lurus KL.
Penyelesaian:
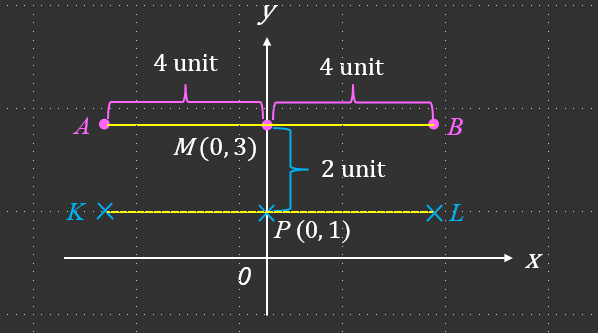
(a)
Titik P berada 2 unit di bawah titik tengah (0, 3) = (0, 1)
Koordinat y adalah sama sepanjang KL.
K berada 4 unit di sebelah kiri titik P = (-4, 1)
L berada 4 unit di sebelah kanan titik P = (4, 1)
(b)
Koordinat titik tengah bagi garis lurus KL = (0, 1)
Jarak AB = KL, iaitu 8 unit dan masing-masing selari dengan paksi-x. Jika titik tengah bagi garis lurus AB ialah (0, 3) dan jarak titik tengah bagi garis lurus AB ke titik tengah bagi garis lurus KL ialah 2 unit ke bawah, hitung
(a) koordinat K dan L.
(b) koordinat titik tengah bagi garis lurus KL.
Penyelesaian:

(a)
Titik P berada 2 unit di bawah titik tengah (0, 3) = (0, 1)
Koordinat y adalah sama sepanjang KL.
K berada 4 unit di sebelah kiri titik P = (-4, 1)
L berada 4 unit di sebelah kanan titik P = (4, 1)
(b)
Koordinat titik tengah bagi garis lurus KL = (0, 1)
Soalan 5:
Diberi P (4, 0) dan Q berada di paksi-y dengan 6 unit ke atas dari paksi-x, hitung
(a) titik tengah bagi garis lurus PQ.
(b) jarak di antara titik P dengan titik tengah bagi garis lurus PQ.
Penyelesaian:
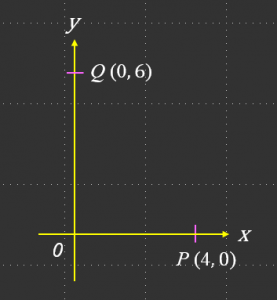
(a)
Diberi Q berada di paksi-y dan 6 unit ke atas dari paksi-x.
Maka, Q = (0, 6)
(b)
Jarak di antara titik P(4, 0) dan titik tengah garis PQ (2, 3)
\(\begin{aligned} & =\sqrt{(4-2)^2+(0-3)^2} \\ & =\sqrt{2^2+(-3)^2} \\ & =\sqrt{4+9} \\ & =\sqrt{13} \\ & =3.6 \text { unit }\end{aligned}\)
Diberi P (4, 0) dan Q berada di paksi-y dengan 6 unit ke atas dari paksi-x, hitung
(a) titik tengah bagi garis lurus PQ.
(b) jarak di antara titik P dengan titik tengah bagi garis lurus PQ.
Penyelesaian:
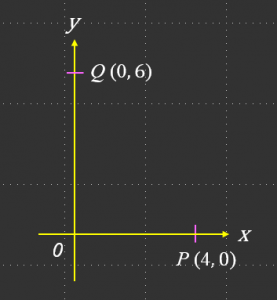
(a)
Diberi Q berada di paksi-y dan 6 unit ke atas dari paksi-x.
Maka, Q = (0, 6)
Titik tengah PQ
\(\begin{aligned} & =\left(\frac{0+4}{2}, \frac{6+0}{2}\right) \\ & =(2,3)\end{aligned}\)
(b)
Jarak di antara titik P(4, 0) dan titik tengah garis PQ (2, 3)
\(\begin{aligned} & =\sqrt{(4-2)^2+(0-3)^2} \\ & =\sqrt{2^2+(-3)^2} \\ & =\sqrt{4+9} \\ & =\sqrt{13} \\ & =3.6 \text { unit }\end{aligned}\)