Permudah ungkapan berikut.
(a) (5b + 3) + 4(3b − a)
(b) 3(4m − 5mn) − 2(8m + mn)
(c) (h − j)2 − 2h(3h − 3j)
(d) (x + y)(x − y) + 2x(x + 2y)
Penyelesaian:
(a)
$$
\begin{aligned}
(5 b+3)+4(3 b-a) & =5 b+3+(4 \times 3 b)+(4 \times-a) \\
& =5 b+3+12 b-4 a \\
& =5 b+12 b-4 a+3 \\
& =17 b-4 a+3
\end{aligned}
$$
(b)
$$
\begin{aligned}
& 3(4 m-5 m n)-2(8 m+m n) \\
& =(3 \times 4 m)+[3 \times(-5 m n)]+(-2 \times 8 m)+(-2 \times m n) \\
& =12 m-15 m n-16 m-2 m n \\
& =12 m-16 m-15 m n-2 m n \\
& =-4 m-17 \mathrm{mn}
\end{aligned}
$$
(c)
$$
\begin{aligned}
& (h-j)^2-2 h(3 h-3 j) \\
& =(h-j)(h-j)+(-2 h \times 3 h)+(-2 h \times-3 j) \\
& =h^2-h j-h j+j^2-6 h^2+6 j h \\
& =h^2-6 h^2-h j-h j+6 j h+j^2 \\
& =-5 h^2+4 h j+j^2
\end{aligned}
$$
(d)
$$
\begin{aligned}
& (x+y)(x-y)+2 x(x+2 y) \\
& =x^2-x y+x y-y^2+2 x^2+4 x y \\
& =x^2+2 x^2-x y+x y+4 x y-y^2 \\
& =3 x^2+4 x y-y^2
\end{aligned}
$$
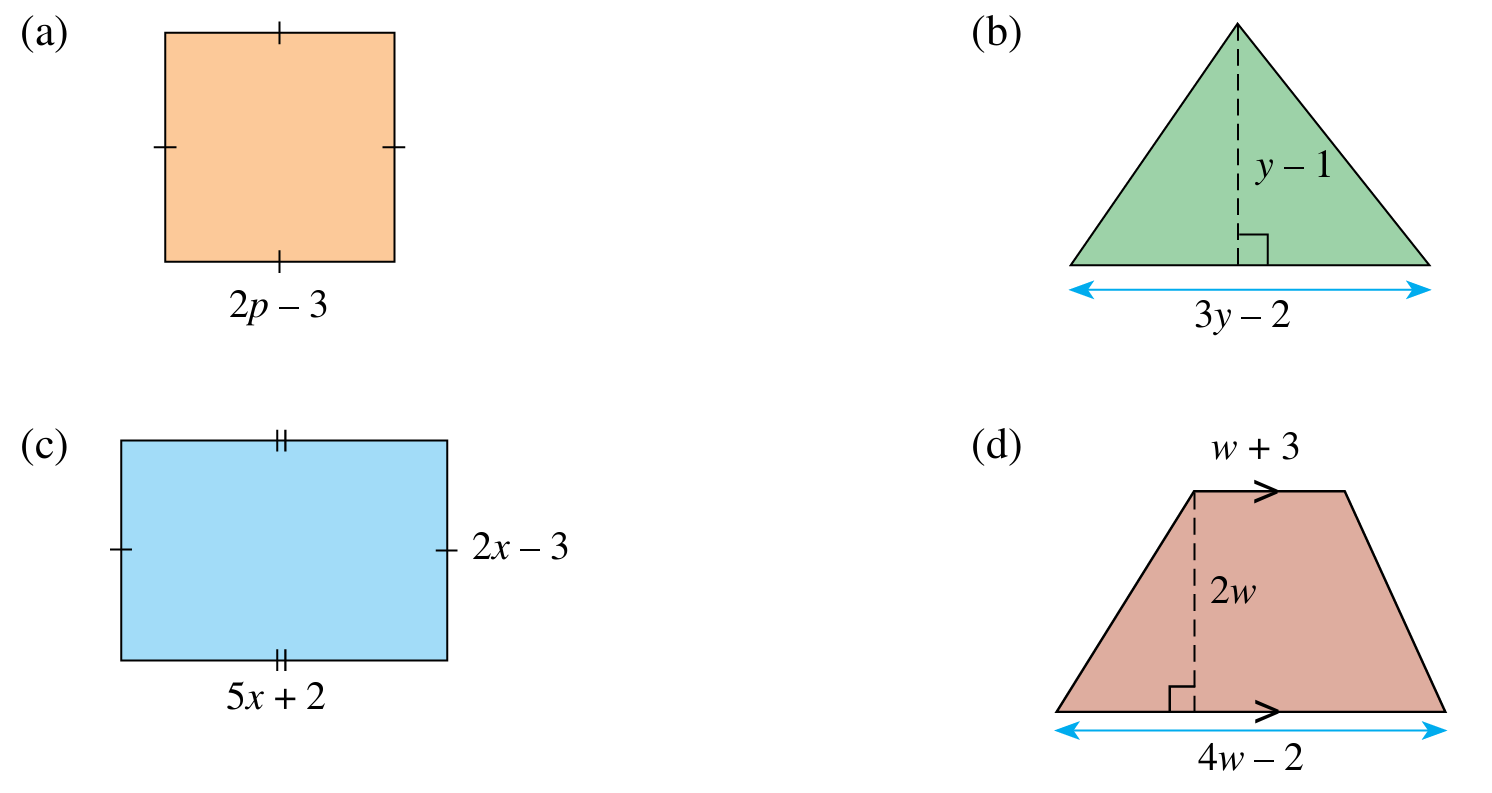
Hitung luas rajah berikut dengan menggunakan ungkapan algebra.
Penyelesaian:
(a)
$$
\begin{aligned}
\text { Luas segi empat sama } & =(2 p-3)(2 p-3) \\
& =4 p^2-6 p-6 p+9 \\
& =4 p^2-12 p+9
\end{aligned}
$$
(b)
$$
\begin{aligned}
\text { Luas segi tiga } & =\frac{1}{2} \times(3 y-2)(y-1) \\
& =\frac{1}{2} \times\left(3 y^2-3 y-2 y+2\right) \\
& =\frac{1}{2} \times\left(3 y^2-5 y+2\right) \\
& =\frac{3}{2} y^2-\frac{5}{2} y+1
\end{aligned}
$$
(c)
$$
\begin{aligned}
\text { Luas segi empat tepat } & =(5 x+2)(2 x-3) \\
& =10 x^2-15 x+4 x-6 \\
& =10 x^2-11 x-6
\end{aligned}
$$
(d)
$$
\begin{aligned}
\text { Luas trapezium } & =\frac{1}{2} \times(w+3+4 w-2)(2 w) \\
& =\frac{1}{2} \times(5 w+1)(2 w) \\
& =\frac{1}{2} \times\left(10 w^2+2 w\right) \\
& =5 w^2+w
\end{aligned}
$$
Hadila berumur 2 tahun lebih muda daripada Kai Yee. Umur bapa Kai Yee ialah kuasa dua umur Hadila. Jika Kai Yee berumur p tahun, hitung jumlah umur mereka bertiga. Ungkapkan jawapan anda dalam bentuk ungkapan algebra.
Penyelesaian:
Umur Kai Yee ialah p tahun
Diberi Hadila berumur 2 tahun lebih muda daripada Kai Yee, maka umur Hadila = p – 2
Umur bapa Kai Yee ialah kuasa dua umur Hadila = (p – 2)2
$$
\begin{aligned}
& \text { Jumlah umur tiga orang } \\
& =\text { Umur Hadila }+ \text { umur Kai Yee }+ \text { umur bapa Kai Yee } \\
& =(p-2)+(p)+(p-2)^2 \\
& =p-2+p+(p-2)(p-2) \\
& =p+p-2+\left[p^2-2 p-2 p+4\right] \\
& =p^2+p+p-2 p-2 p-2+4 \\
& =p^2-2 p+2
\end{aligned}
$$
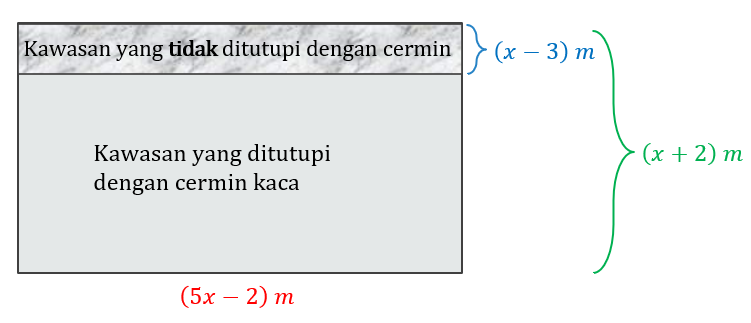
Sebuah permukaan meja berbentuk segi empat tepat mempunyai panjang (5x − 2) meter dan lebar (x + 2) meter. Encik Phillip ingin meletakkan cermin kaca di atas meja tersebut. Lebar meja yang tidak ditutupi dengan cermin ialah (x − 3) meter. Ungkapkan luas permukaan meja yang tidak ditutupi dengan cermin kaca tersebut.
Penyelesaian:
$$
\begin{aligned}
&\text { Kawasan yang tidak ditutupi dengan cermin kaca }\\
&\begin{aligned}
& =(5 x-2)(x-3) \\
& =5 x^2-15 x-2 x+6 \\
& =\left(5 x^2-17 x+6\right) m^2
\end{aligned}
\end{aligned}
$$
Hitungkan panjang LM dalam sebutan y.
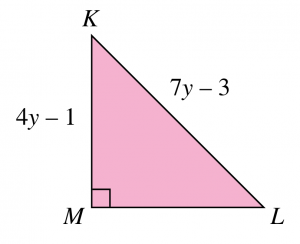
Penyelesaian:
$$
\begin{aligned}
&\text { Dengan menggunakan teorem Pythagoras, }\\
&\begin{aligned}
& K L^2=K M^2+L M^2 \\
& L M^2=K L^2-K M^2 \\
& L M^2=(7 y-3)^2-(4 y-1)^2 \\
& L M^2=(7 y-3)(7 y-3)-(4 y-1)(4 y-1) \\
& L M^2=49 y^2-21 y-21 y+9-\left[16 y^2-4 y-4 y+1\right] \\
& L M^2=49 y^2-21 y-21 y+9-16 y^2+4 y+4 y-1 \\
& L M^2=49 y^2-16 y^2-21 y-21 y+4 y+4 y+9-1 \\
& L M^2=33 y^2-34 y+8 \\
& L M=\sqrt{33 y^2-34 y+8}
\end{aligned}
\end{aligned}
$$