Soalan 1:
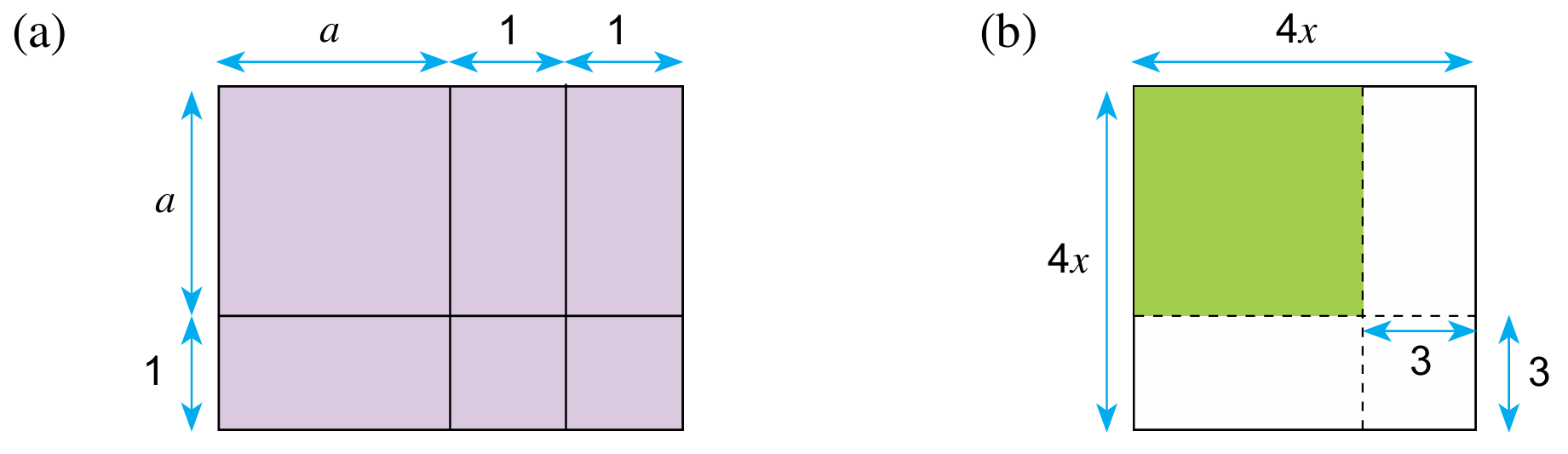
Berdasarkan jubin algebra berikut, tulis luas kawasan berlorek dalam bentuk pendaraban dua ungkapan algebra.
Penyelesaian:
(a)
$$
\begin{aligned}
\text { Luas kawasan berlorek } & =\text { panjang } \times \text { lebar } \\
& =(a+1+1)(a+1) \\
& =(a+2)(a+1)
\end{aligned}
$$
(b)
$$
\begin{aligned}
\text { Luas kawasan berlorek } & =\text { panjang } \times \text { lebar } \\
& =(4 x-3)(4 x-3)
\end{aligned}
$$
Berdasarkan jubin algebra berikut, tulis luas kawasan berlorek dalam bentuk pendaraban dua ungkapan algebra.
Penyelesaian:
(a)
$$
\begin{aligned}
\text { Luas kawasan berlorek } & =\text { panjang } \times \text { lebar } \\
& =(a+1+1)(a+1) \\
& =(a+2)(a+1)
\end{aligned}
$$
(b)
$$
\begin{aligned}
\text { Luas kawasan berlorek } & =\text { panjang } \times \text { lebar } \\
& =(4 x-3)(4 x-3)
\end{aligned}
$$
Soalan 2:
Kembangkan ungkapan algebra berikut.
(a) 3(x + 2)
(b) 4(8x − 3)
(c) 2(a + 5)
(d) p(6p − 8)
(e) − r/8 (2s − 8)
(f) −2(pr − 2pq)
(g) 3(5bc − 6)
(h) 7(2ef + 3e)
(i) 8g(2 + gh)
(c)
$$
\begin{aligned}
& 2(a+5) \\
& =(2 \times a)+(2 \times 5) \\
& =2 a+10
\end{aligned}
$$
(d)
$$
\begin{aligned}
& p(6 p-8) \\
& =(p \times 6 p)+(p \times-8) \\
& =6 p^2-8 p
\end{aligned}
$$
(e)
$$
\begin{aligned}
& -\frac{r}{8}(2 s-8) \\
= & \left(-\frac{r}{8} \times 2 s\right)+\left(-\frac{r}{8} \times-8\right) \\
= & -\frac{r s}{4}+r
\end{aligned}
$$
(f)
$$
\begin{aligned}
& -2(p r-2 p q) \\
& =(-2 \times p r)+(-2 \times-2 p q) \\
& =-2 p r+4 p q
\end{aligned}
$$
(g)
$$
\begin{aligned}
& 3(5 b c-6) \\
& =(3 \times 5 b c)+(3 \times-6) \\
& =15 b c-18
\end{aligned}
$$
(h)
$$
\begin{aligned}
& 7(2 e f+3 e) \\
& =(7 \times 2 e f)+(7 \times 3 e) \\
& =14 e f+21 e
\end{aligned}
$$
(i)
$$
\begin{aligned}
& 8 g(2+g h) \\
& =(8 g \times 2)+(8 g \times g h) \\
& =16 g+8 g^2 h
\end{aligned}
$$
Kembangkan ungkapan algebra berikut.
(a) 3(x + 2)
(b) 4(8x − 3)
(c) 2(a + 5)
(d) p(6p − 8)
(e) − r/8 (2s − 8)
(f) −2(pr − 2pq)
(g) 3(5bc − 6)
(h) 7(2ef + 3e)
(i) 8g(2 + gh)
Penyelesaian:
(a)
$$
\begin{aligned}
& 3(x+2) \\
& =(3 \times x)+(3 \times 2) \\
& =3 x+6
\end{aligned}
$$
(b)
$$
\begin{aligned}
& 4(8 x-3) \\
& =(4 \times 8 x)+(4 \times-3) \\
& =32 x-12
\end{aligned}
$$
(c)
$$
\begin{aligned}
& 2(a+5) \\
& =(2 \times a)+(2 \times 5) \\
& =2 a+10
\end{aligned}
$$
(d)
$$
\begin{aligned}
& p(6 p-8) \\
& =(p \times 6 p)+(p \times-8) \\
& =6 p^2-8 p
\end{aligned}
$$
(e)
$$
\begin{aligned}
& -\frac{r}{8}(2 s-8) \\
= & \left(-\frac{r}{8} \times 2 s\right)+\left(-\frac{r}{8} \times-8\right) \\
= & -\frac{r s}{4}+r
\end{aligned}
$$
(f)
$$
\begin{aligned}
& -2(p r-2 p q) \\
& =(-2 \times p r)+(-2 \times-2 p q) \\
& =-2 p r+4 p q
\end{aligned}
$$
(g)
$$
\begin{aligned}
& 3(5 b c-6) \\
& =(3 \times 5 b c)+(3 \times-6) \\
& =15 b c-18
\end{aligned}
$$
(h)
$$
\begin{aligned}
& 7(2 e f+3 e) \\
& =(7 \times 2 e f)+(7 \times 3 e) \\
& =14 e f+21 e
\end{aligned}
$$
(i)
$$
\begin{aligned}
& 8 g(2+g h) \\
& =(8 g \times 2)+(8 g \times g h) \\
& =16 g+8 g^2 h
\end{aligned}
$$
Soalan 3:
Kembangkan ungkapan algebra berikut.
(a) (a + 1)(a + 2)
(b) (x − 5)(x + 4)
(c) (2 + m)(5 − m)
(d) (3p − 2)(4p − 1)
(e) (3r − 2)(4r − 1)
(f) (2r + s)(4r − 3s)
(g) (2d − ½b)(3d − ½b)
(h) (r − 3s)2
(i) (4e − 3)2
(c)
$$
\begin{aligned}
&(2+m)(5-m)\\
&\begin{aligned}
& =2(5-m)+m(5-m) \\
& =10-2 m+5 m-m^2 \\
& =10+3 m-m^2
\end{aligned}
\end{aligned}
$$
(d)
$$
\begin{aligned}
& (3 p-2)(4 p-1) \\
& =3 p(4 p-1)-2(4 p-1) \\
& =12 p^2-3 p-8 p+2 \\
& =12 p^2-11 p+2
\end{aligned}
$$
(e)
$$
\begin{aligned}
& (3 r-2)(4 r-1) \\
& =3 r(4 r-1)-2(4 r-1) \\
& =12 r^2-3 r-8 r+2 \\
& =12 r^2-11 r+2
\end{aligned}
$$
(f)
$$
\begin{aligned}
&(2 r+s)(4 r-3 s)\\
&\begin{aligned}
& =2 r(4 r-3 s)+s(4 r-3 s) \\
& =8 r^2-6 r s+4 r s-3 s^2 \\
& =8 r^2-3 s^2-2 r s
\end{aligned}
\end{aligned}
$$
(g)
$$
\begin{aligned}
& \left(2 d-\frac{1}{2} b\right)\left(3 d-\frac{1}{2} b\right) \\
& =2 d\left(3 d-\frac{1}{2} b\right)-\frac{1}{2} b\left(3 d-\frac{1}{2} b\right) \\
& =6 d^2-b d-\frac{3}{2} b d+\frac{1}{4} b^2 \\
& =6 d^2-\frac{5}{2} b d+\frac{1}{4} b^2
\end{aligned}
$$
(h)
$$
\begin{aligned}
& (r-3 s)^2 \\
& =(r-3 s)(r-3 s) \\
& =r^2-3 r s-3 r s+9 s^2 \\
& =r^2-6 r s+9 s^2
\end{aligned}
$$
(i)
$$
\begin{aligned}
& (4 e-3)^2 \\
& =(4 e-3)(4 e-3) \\
& =16 e^2-12 e-12 e+9 \\
& =16 e^2-24 e+9
\end{aligned}
$$
Kembangkan ungkapan algebra berikut.
(a) (a + 1)(a + 2)
(b) (x − 5)(x + 4)
(c) (2 + m)(5 − m)
(d) (3p − 2)(4p − 1)
(e) (3r − 2)(4r − 1)
(f) (2r + s)(4r − 3s)
(g) (2d − ½b)(3d − ½b)
(h) (r − 3s)2
(i) (4e − 3)2
Penyelesaian:
(a)
$$
\begin{aligned}
&(a+1)(a+2)\\
&\begin{aligned}
& =a(a+2)+1(a+2) \\
& =a^2+2 a+a+2 \\
& =a^2+3 a+2
\end{aligned}
\end{aligned}
$$
(b)
$$
\begin{aligned}
&(x-5)(x+4)\\
&\begin{aligned}
& =x(x+4)-5(x+4) \\
& =x^2+4 x-5 x-20 \\
& =x^2-x-20
\end{aligned}
\end{aligned}
$$
(c)
$$
\begin{aligned}
&(2+m)(5-m)\\
&\begin{aligned}
& =2(5-m)+m(5-m) \\
& =10-2 m+5 m-m^2 \\
& =10+3 m-m^2
\end{aligned}
\end{aligned}
$$
(d)
$$
\begin{aligned}
& (3 p-2)(4 p-1) \\
& =3 p(4 p-1)-2(4 p-1) \\
& =12 p^2-3 p-8 p+2 \\
& =12 p^2-11 p+2
\end{aligned}
$$
(e)
$$
\begin{aligned}
& (3 r-2)(4 r-1) \\
& =3 r(4 r-1)-2(4 r-1) \\
& =12 r^2-3 r-8 r+2 \\
& =12 r^2-11 r+2
\end{aligned}
$$
(f)
$$
\begin{aligned}
&(2 r+s)(4 r-3 s)\\
&\begin{aligned}
& =2 r(4 r-3 s)+s(4 r-3 s) \\
& =8 r^2-6 r s+4 r s-3 s^2 \\
& =8 r^2-3 s^2-2 r s
\end{aligned}
\end{aligned}
$$
(g)
$$
\begin{aligned}
& \left(2 d-\frac{1}{2} b\right)\left(3 d-\frac{1}{2} b\right) \\
& =2 d\left(3 d-\frac{1}{2} b\right)-\frac{1}{2} b\left(3 d-\frac{1}{2} b\right) \\
& =6 d^2-b d-\frac{3}{2} b d+\frac{1}{4} b^2 \\
& =6 d^2-\frac{5}{2} b d+\frac{1}{4} b^2
\end{aligned}
$$
(h)
$$
\begin{aligned}
& (r-3 s)^2 \\
& =(r-3 s)(r-3 s) \\
& =r^2-3 r s-3 r s+9 s^2 \\
& =r^2-6 r s+9 s^2
\end{aligned}
$$
(i)
$$
\begin{aligned}
& (4 e-3)^2 \\
& =(4 e-3)(4 e-3) \\
& =16 e^2-12 e-12 e+9 \\
& =16 e^2-24 e+9
\end{aligned}
$$