2.1.2 Pemfaktoran Ungkapan Algebra


2.1.2 Pemfaktoran Ungkapan Algebra
 
(A) Pemfaktoran ungkapan algebra yang berbentuk ax2+ bx + c, b = 0 atau c = 0
1.   Pemfaktoran ungkapan algebra ialah proses mencari dua ungkapan linear yang hasil darabnya sama dengan ungkapan kuadratik itu.
2.  Ungkapan-ungkapan algebra ax2 + c dan ax2 + bx yang mengandungi dua sebutan boleh difaktorkan dengan mencari faktor sepunya bagi kedua-dua sebutan itu.

Contoh 1:
Faktorkan setiap yang berikut:
(a)  2x2 + 6
(b)  7p2 – 3p
(c)  6x2 – 9x

Penyelesaian:
(a)  2x2 + 6 = 2(x2 + 3) ← (2 ialah faktor sepunya)
(b)  7p2 – 3p = p(7p – 3) ← (p ialah faktor sepunya)
(c)  6x2 – 9x = 3x (2x – 3) ← (3x ialah faktor sepunya)


(B) Memfaktorkan ungkapan algebra yang berbentuk ax2– c , a dan c adalah nombor kuasa dua sempurna

Contoh 2:
(a) 9p2 – 16
(b) 25x2 – 1
(c) 1 4 − 1 25 x 2  

Penyelesaian:
(a)  9p2 – 16 = (3p)2 – 42 = (3p – 4) (3p + 4)
(b)  25x2 – 1 = (5x)2 – 12 = (5x – 1) (5x + 1)
(c) 
1 4 − 1 25 x 2 = ( 1 2 ) 2 − ( 1 5 x ) 2 = ( 1 2 − 1 5 x ) ( 1 2 + 1 5 x )  



(C) Memfaktorkan ungkapan algebra berbentuk ax2+ bx + c, di mana a ≠ 0, b ≠ 0 dan c ≠ 0

Contoh 3:
Faktorkan setiap yang berikut:
(a)  3y2 + 2y – 8
(b)  4x2 – 12x + 9

Penyelesaian:
Pemfaktoran dengan kaedah darab silang.

(a)


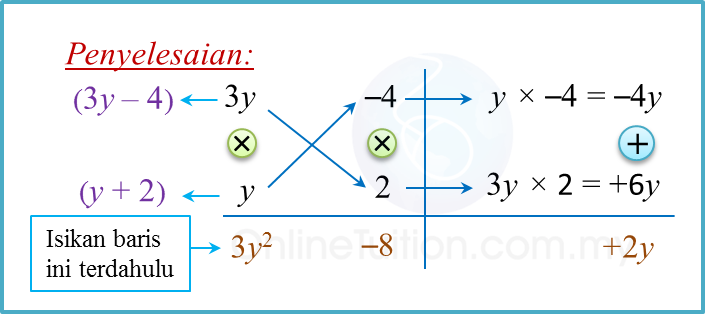
3y2+ 2y – 8 = (3y – 4) (y + 2)


(b)


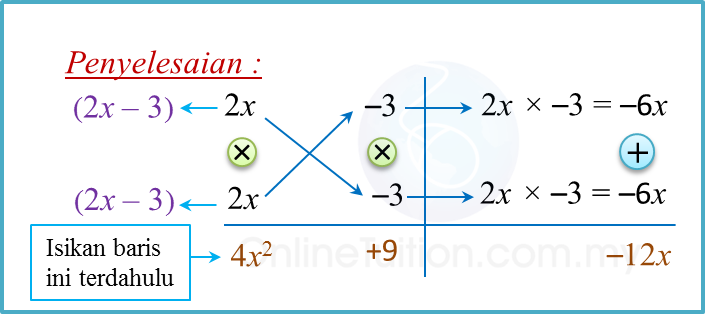
4x2– 12x + 9 = (2x – 3) (2x – 3)

Leave a Comment