Soalan 4:
(a) Diberi x = 5 dan y = –2, cari nilai bagi xy + x/2 – 6y.
(b) Diberi a = 7, b = 3 dan c = –4, cari nilai bagi 3(b – a) – 5ac + 14
Penyelesaian:
(a)
Diberi \(x=5\) dan \(y=-2\) \[ \begin{aligned} & x y+\frac{x}{2}-6 y \\ & =(5)(-2)+\frac{5}{2}-6(-2) \\ & =-10+\frac{5}{2}+12 \\ & =\frac{-20}{2}+\frac{5}{2}+\frac{24}{2} \\ & =\frac{-20+5}{2}+24 \\ & =\frac{9}{2} \\ & =4 \frac{1}{2} \end{aligned} \]
(b)
Diberi \(a=7, b=3\) dan \(c=-4\) \[ \begin{aligned} & 3(b-a)-5 a c+14 \\ = & 3(3-7)-5(7)(-4)+14 \\ = & 3(-4)-5(-28)+14 \\ = & 12+140+14 \\ = & 142 \end{aligned} \]
(a) Diberi x = 5 dan y = –2, cari nilai bagi xy + x/2 – 6y.
(b) Diberi a = 7, b = 3 dan c = –4, cari nilai bagi 3(b – a) – 5ac + 14
Penyelesaian:
(a)
Diberi \(x=5\) dan \(y=-2\) \[ \begin{aligned} & x y+\frac{x}{2}-6 y \\ & =(5)(-2)+\frac{5}{2}-6(-2) \\ & =-10+\frac{5}{2}+12 \\ & =\frac{-20}{2}+\frac{5}{2}+\frac{24}{2} \\ & =\frac{-20+5}{2}+24 \\ & =\frac{9}{2} \\ & =4 \frac{1}{2} \end{aligned} \]
(b)
Diberi \(a=7, b=3\) dan \(c=-4\) \[ \begin{aligned} & 3(b-a)-5 a c+14 \\ = & 3(3-7)-5(7)(-4)+14 \\ = & 3(-4)-5(-28)+14 \\ = & 12+140+14 \\ = & 142 \end{aligned} \]
Soalan 5:
Azlan ada n keping syiling yang terdiri daripada x keping syiling 10 sen, 3x keping syiling 20 sen dan selebihnya 50 sen di dalam tabung duit.
(a) Nyatakan ungkapan bagi bilangan syiling 50 sen yang ada di dalam tabung duit.
(b) Cari jumlah wang di dalam tabung duit jika x = 6 dan bilangan syiling 50 sen adalah dua kali bilangan syiling 20 sen.
Penyelesaian:
(a)
Bilangan syiling 50 sen
= Jumlah kepingan syiling – kepingan syiling 10 sen – kepingan syiling 20 sen
= n – x – 3x
= n – 4x
(b)
Diberi bahawa bilangan syiling 50 sen adalah dua kali bilangan syiling 20 sen.
Maka, bilangan syiling 50 sen = 2 × 3x = 6x
Apabila \(x=6\), jumlah wang di dalam tabung duit \[ \begin{aligned} & =x(10 \text { sen })+3 x(20 \text { sen })+6 x(50 \text { sen }) \\ & =6(10 \text { sen })+3(6)(20 \text { sen })+6(6)(50 \text { sen }) \\ & =60 \text { sen }+360 \text { sen }+1800 \text { sen } \\ & =2220 \text { sen } \\ & =\text { RM } 22.20 \end{aligned} \]
Azlan ada n keping syiling yang terdiri daripada x keping syiling 10 sen, 3x keping syiling 20 sen dan selebihnya 50 sen di dalam tabung duit.
(a) Nyatakan ungkapan bagi bilangan syiling 50 sen yang ada di dalam tabung duit.
(b) Cari jumlah wang di dalam tabung duit jika x = 6 dan bilangan syiling 50 sen adalah dua kali bilangan syiling 20 sen.
Penyelesaian:
(a)
Bilangan syiling 50 sen
= Jumlah kepingan syiling – kepingan syiling 10 sen – kepingan syiling 20 sen
= n – x – 3x
= n – 4x
(b)
Diberi bahawa bilangan syiling 50 sen adalah dua kali bilangan syiling 20 sen.
Maka, bilangan syiling 50 sen = 2 × 3x = 6x
Apabila \(x=6\), jumlah wang di dalam tabung duit \[ \begin{aligned} & =x(10 \text { sen })+3 x(20 \text { sen })+6 x(50 \text { sen }) \\ & =6(10 \text { sen })+3(6)(20 \text { sen })+6(6)(50 \text { sen }) \\ & =60 \text { sen }+360 \text { sen }+1800 \text { sen } \\ & =2220 \text { sen } \\ & =\text { RM } 22.20 \end{aligned} \]
Soalan 6:
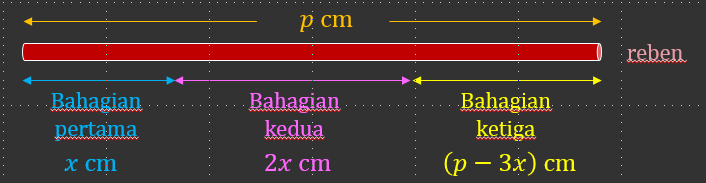
Seutas reben sepanjang p cm dipotong kepada tiga bahagian. Panjang bahagian pertama dan bahagian kedua masing-masing ialah x cm dan 2x cm.
(a) Tulis satu ungkapan bagi panjang bahagian ketiga.
(b) Jika x = 10 dan panjang bahagian kedua adalah empat kali panjang bahagian ketiga, hitung nilai p.
Penyelesaian:
(a)
Panjang bahagian ketiga
= (p – x – 2x) cm
= (p – 3x) cm
(b)
Diberi x = 10 dan panjang bahagian kedua adalah empat kali panjang bahagian ketiga,
\[ \begin{aligned} 2 x & =4(p-3 x) \\ 2 x & =4 p-12 x \\ -4 p & =-12 x-2 x \\ -4 p & =-14 x \\ \frac{-4 p}{-4} & =\frac{-14 x}{-4} \\ p & =\frac{7(10)}{2} \\ & =35 \end{aligned} \]
Seutas reben sepanjang p cm dipotong kepada tiga bahagian. Panjang bahagian pertama dan bahagian kedua masing-masing ialah x cm dan 2x cm.
(a) Tulis satu ungkapan bagi panjang bahagian ketiga.
(b) Jika x = 10 dan panjang bahagian kedua adalah empat kali panjang bahagian ketiga, hitung nilai p.
Penyelesaian:

(a)
Panjang bahagian ketiga
= (p – x – 2x) cm
= (p – 3x) cm
(b)
Diberi x = 10 dan panjang bahagian kedua adalah empat kali panjang bahagian ketiga,
\[ \begin{aligned} 2 x & =4(p-3 x) \\ 2 x & =4 p-12 x \\ -4 p & =-12 x-2 x \\ -4 p & =-14 x \\ \frac{-4 p}{-4} & =\frac{-14 x}{-4} \\ p & =\frac{7(10)}{2} \\ & =35 \end{aligned} \]