Soalan 11:
Dalam rajah di bawah, ABC ialah sebuah segi tiga.
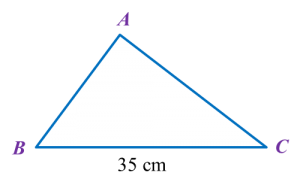

Sisi-sisi segi tiga adalah dalam nisbah AB : BC : CA = 4 : 7 : 6.
Cari beza panjang, dalam cm, antara AB dan CA.
Penyelesaian:
Beza panjang antara AB dan CA
= 30 – 20
= 10 cmSoalan 12:
Rajah di bawah menunjukkan dua bakul, A dan B, yang diisi dengan gula-gula.
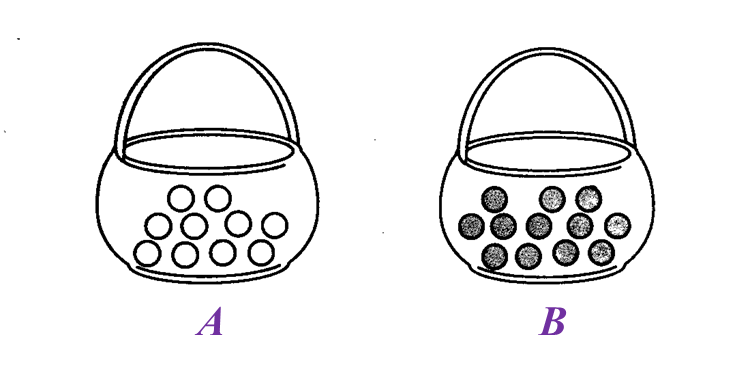 (a) Nyatakan nisbah bilangan gula-gula dalam bakul A kepada bilangan gula-gula dalam bakul B.
(a) Nyatakan nisbah bilangan gula-gula dalam bakul A kepada bilangan gula-gula dalam bakul B.
(b) Sekiranya 20 biji gula-gula ditambahkan ke dalam bakul A, hitung bilangan gula-gula yang perlu ditambahkan ke dalam bakul B supaya nisbah di (a) tidak berubah.
Penyelesaian:
(a)
Nisbah bilangan gula-gula dalam bakul A kepada bilangan gula-gula dalam bakul B
= 10 : 12
= 5 : 6
(b)
Sekiranya 20 biji gula-gula ditambahkan ke dalam bakul A, bilangan gula-gula yang perlu ditambahkan ke dalam bakul B supaya nisbah 5 : 6 tidak berubah
= 20 ÷ 5 × 6
= 4 × 6
= 24
Rajah di bawah menunjukkan dua bakul, A dan B, yang diisi dengan gula-gula.
 (a) Nyatakan nisbah bilangan gula-gula dalam bakul A kepada bilangan gula-gula dalam bakul B.
(a) Nyatakan nisbah bilangan gula-gula dalam bakul A kepada bilangan gula-gula dalam bakul B.(b) Sekiranya 20 biji gula-gula ditambahkan ke dalam bakul A, hitung bilangan gula-gula yang perlu ditambahkan ke dalam bakul B supaya nisbah di (a) tidak berubah.
Penyelesaian:
(a)
Nisbah bilangan gula-gula dalam bakul A kepada bilangan gula-gula dalam bakul B
= 10 : 12
= 5 : 6
(b)
Sekiranya 20 biji gula-gula ditambahkan ke dalam bakul A, bilangan gula-gula yang perlu ditambahkan ke dalam bakul B supaya nisbah 5 : 6 tidak berubah
= 20 ÷ 5 × 6
= 4 × 6
= 24
Soalan 13:
Karim membina dua buah Menara daripada blok mainan yang sama saiz seperti yang ditunjukkan pada Rajah di bawah.
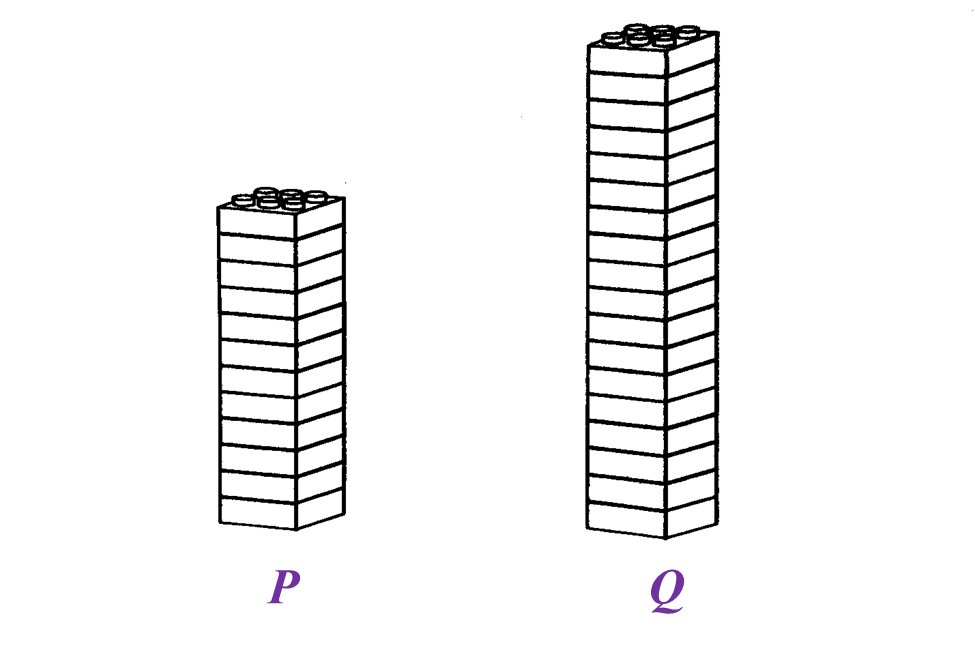 (a) Nyatakan nisbah bilangan blok mainan Menara P kepada bilangan blok mainan di Menara Q.
(a) Nyatakan nisbah bilangan blok mainan Menara P kepada bilangan blok mainan di Menara Q.
(b) Sebilangan blok mainan yang perlu dikeluarkan daripada setiap Menara supaya nisbah di (a) kekal. Cari jumlah bilangan blok mainan yang perlu dikeluarkan dari setiap Menara itu.
Penyelesaian:
(a)
Menara P : Menara Q
= 12 : 18
= 2 : 3
(b)
Jadikan bilangan blok mainan yang perlu dikeluarkan dari setiap Menara itu = n
Jumlah bilangan blok mainan yang perlu dikeluarkan
= 2n + 3n
2(1) + 3(1) = 2 + 3 = 5 → (2 blok mainan dari menara P, 3 blok mainan dari menara Q)
2(2) + 3(2) = 4 + 6 = 10 → (4 blok mainan dari menara P, 6 blok mainan dari menara Q)
2(3) + 3(3) = 6 + 9 = 15 → (6 blok mainan dari menara P, 9 blok mainan dari menara Q)
2(4) + 3(4) = 8 + 12 = 20 → (8 blok mainan dari menara P, 12 blok mainan dari menara Q)
2(5) + 3(5) = 10 + 15 = 25 → (10 blok mainan dari menara P, 15 blok mainan dari menara Q)
Karim membina dua buah Menara daripada blok mainan yang sama saiz seperti yang ditunjukkan pada Rajah di bawah.
 (a) Nyatakan nisbah bilangan blok mainan Menara P kepada bilangan blok mainan di Menara Q.
(a) Nyatakan nisbah bilangan blok mainan Menara P kepada bilangan blok mainan di Menara Q.(b) Sebilangan blok mainan yang perlu dikeluarkan daripada setiap Menara supaya nisbah di (a) kekal. Cari jumlah bilangan blok mainan yang perlu dikeluarkan dari setiap Menara itu.
Penyelesaian:
(a)
Menara P : Menara Q
= 12 : 18
= 2 : 3
(b)
Jadikan bilangan blok mainan yang perlu dikeluarkan dari setiap Menara itu = n
Jumlah bilangan blok mainan yang perlu dikeluarkan
= 2n + 3n
2(1) + 3(1) = 2 + 3 = 5 → (2 blok mainan dari menara P, 3 blok mainan dari menara Q)
2(2) + 3(2) = 4 + 6 = 10 → (4 blok mainan dari menara P, 6 blok mainan dari menara Q)
2(3) + 3(3) = 6 + 9 = 15 → (6 blok mainan dari menara P, 9 blok mainan dari menara Q)
2(4) + 3(4) = 8 + 12 = 20 → (8 blok mainan dari menara P, 12 blok mainan dari menara Q)
2(5) + 3(5) = 10 + 15 = 25 → (10 blok mainan dari menara P, 15 blok mainan dari menara Q)